线性模型笔记
本文最后更新于:几秒前
《神经网络与机器学习》第三章笔记
线性分类问题
二分类
$$
x^\in\mathbb R^D,y^\in{0,1}
$$
多分类
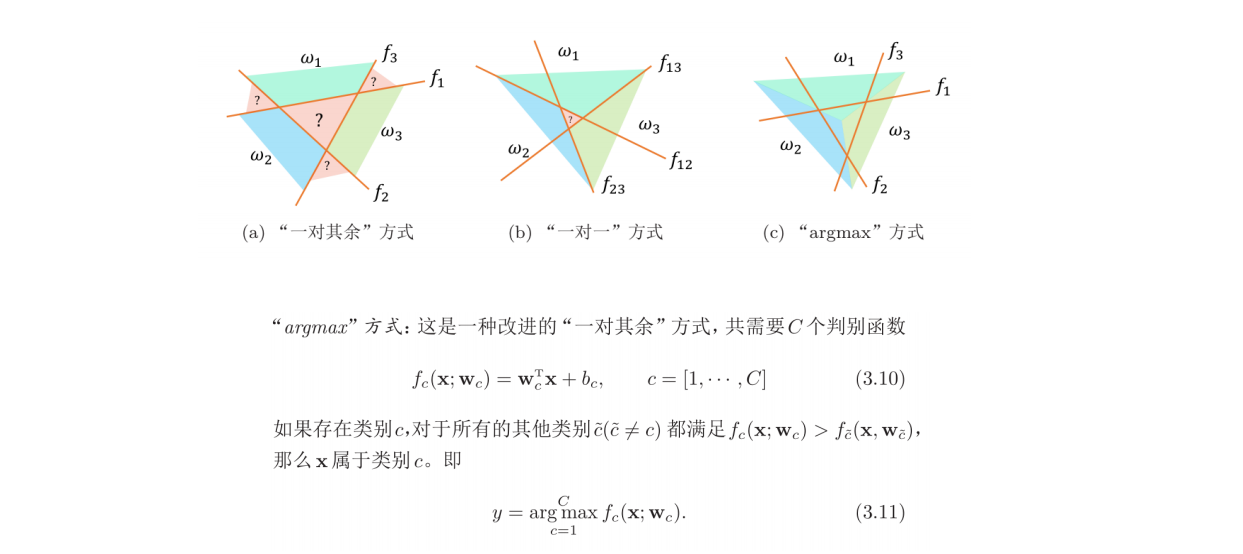
信息论基础
熵
在信息论中,熵用来衡量一个随机事件的不确定性,自信息用于衡量一个随机事件所携带的信息量,一般来说概率越小,其携带的可能信息越多,即:
$$
I(x) = -log(p(x))
$$
自信息本身具有可加性,而熵基于自信息,是随机变量X的自信息的期望,熵越高,其随机变量的信息越多。
$$
H(x)=\mathbb E_X[I(x)]=\mathbb E_X[-logp(x)] = -\displaystyle\sum_{x \in \mathcal X}p(x)log(p(x))
$$
在对分布$q(y)$的符号进行编码时,其熵$H(q)$也是理论上的最优平均编码长度,这种编码方式称为熵编码。
交叉熵
交叉熵是按照概率分布$q$的最优编码对真实分布为$p$的信息进行编码的长度。
$$
H(p,q)=\mathbb E_p[-logq(x)]=-\displaystyle \sum_xp(x)logq(x)
$$
当$p=q$时,交叉熵==熵,而熵编码是最优的编码方式,即$H(p,q)$最小的方式,因此在给定了$q$的情况下,如果$p$和$q$越接近,交叉熵就会越小。
KL散度
KL散度使用概率分布$q$来近似$p$时所造成的信息损失量,是按照概率分布$q$的最优编码对真实分布为$p$的信息进行编码,其平均编码长度(即交叉熵)$H(p,q)$和$p$的最优平均编码长度(即熵)$H(p)$之间的差异。
$$
KL(p,q) = H(p,q)-H(p)=\displaystyle \sum_xp(x) log{p(x)\over q(x)}
$$
交叉熵损失
$$
\begin{align}
D_ {KL}(p_r(y|x) || p_\theta(y|x)) & = \displaystyle \sum_{y=0}^1 p_r(y|x)log{p_r(y|x) \over p\theta(y|x)}
\propto -\displaystyle \sum_{y=0}^1p_ r(y|x)logp_\theta(y|x) \\\\
& = -I(y^*=1)logp_\theta(y=1|x)-I(y^*=0)logp_\theta(y=0|x) \\\\
& = -y^* logp_ \theta(y=1|x) - (1- y^*)logp_ \theta (y=0|x) \\\\
& = -logp_\theta(y^*|x)
\end{align}
$$
Logistic回归
首先确定一个观点:可以将分类问题看作是一种条件概率估计问题,因此可以引入一个非线性函数$g$来将线性函数的值域压缩到条件概率的(0,1)之间,来表示分类问题的概率,即:
$$
p(y=1|\pmb x)= g(f(\pmb x;\pmb w))
$$
为了能让$g$函数进一步可微分,我们采用logistic函数(以$\sigma(x)$表示)来代替原有的二分类的分段函数
$$
\sigma(x) = {1 \over {1+exp(-x)}}
$$
在线性分类中$y=\pmb w\top \pmb x$需要进入分类,将其看作条件概率,即:
$$
p_\theta(y=1|\pmb x) = \sigma(\pmb w\top\pmb x) = {1 \over 1+exp(-\pmb w\top\pmb x)} \\
p_\theta(y=0|\pmb x) = 1-\sigma(\pmb w\top\pmb x) = {exp(-\pmb w\top\pmb x) \over {1+exp(-\pmb w\top\pmb x)}}
$$
而对于一个样本$(x,y^*)$,其真实条件概率为
$$
p(y=1|\pmb x) = y^* \\
p(y=0|\pmb x) = 1-y^*
$$
对这两者的差异进行衡量可以采用上文所提到的交叉熵损失,即
$$
\begin{align}
KL (p_ r,p_ \theta) = & = -I (y^*=1)\ log\ p_ \theta (y=1|x) - I(y^*=0)\ log\ p_ \theta (y=0|x)
\end{align}
$$
所以Logistic回归的损失函数可以写作:
$$
\mathcal R(\pmb w)=-{1\over N}\displaystyle \displaystyle\sum_{i=1}^N (y^{(i)}log(\sigma(\pmb w\top \pmb x^{(i)})) +(1-y^{(i)})log(1-\sigma(\pmb w\top \pmb x^{(i)})))
$$
令$\sigma(\pmb w\top\pmb x)=\hat y$其在参数$\pmb w$上求梯度可得
$$
\begin{align}
{\partial\mathcal R(\pmb w) \over \partial\pmb w} & = -C_1 \ {1\over N}\displaystyle\sum_{i=1}^N(y^{(i)}{1\over \hat y^{(i)}}\pmb x^{(i)} - (1-y^{(i)}){1\over {1-\hat y^{(i)}}}\pmb x^{(i)}) \\\\
& = -C_2 \ {1\over N}\displaystyle\sum_{i=1}^N(y^{(i)}{ \hat y^{(i)} (1-\hat y^{(i)})\over \hat y^{(i)}}\pmb x^{(i)} - (1-y^{(i)}){\hat y^{(i)} (1-\hat y^{(i)})\over {1-\hat y^{(i)}}}\pmb x^{(i)}) \\\\
& = -C_2 \ {1\over N}\displaystyle\sum_{i=1}^N(y^{(i)}(1-\hat y^{(i)})\pmb x^{(i)} - (1-y^{(i)})\hat y^{(i)}\pmb x^{(i)})\\\\
& = -C_2 \ {1\over N}\displaystyle\sum_{i=1}^N(y^{(i)} - \hat y^{(i)})x^{(i)}
\end{align}
$$
因此,梯度下降的参数更新将从梯度的反方向进行。即$\pmb w_{t+1} \leftarrow \pmb w_{t+1} + \alpha {1\over N}\displaystyle\sum_{i=1}^N(y^{(i)} - \hat y^{(i)})x^{(i)}$
Softmax回归
softmax从logistic回归出发,基于多分类问题进行,基于多分类问题的argmax法可得
$$
y=\arg \max_{c=1}^C f_c(\pmb x;\pmb w_c)
$$
利用softmax函数,可以得到$y=c$的条件概率为
$$
P(y=c|\pmb x)=softmax(\pmb w_c^\top \pmb x) = {exp(\pmb w_c^\top \pmb x) \over \displaystyle \sum_{i=1}^Cexp(\pmb w_i^\top \pmb x)}
$$
其交叉熵损失函数依然是真实标签和条件概率的交叉熵,即
$$
Loss(\pmb y,f(\pmb x,\theta)) = -\displaystyle \sum_{c=1}^C y_c\ log f_c(\pmb x,\theta)
$$
梯度下降的方式和logistic很相似,是两个标签向量相减
$$
{\partial\mathcal R(\pmb w) \over \partial\pmb w} = {1\over N}\displaystyle\sum_{i=1}^N({\pmb y}^{(i)} - \hat {\pmb y}^{(i)})x^{(i)}
$$
感知机
感知机是一种错误驱动的在线学习算法,初始化$\pmb w$为全零向量,每次分错一个样本$(\pmb x,y)$时,即当$y\pmb w^\top\pmb x<0$时,用这个样本来更新整体的权重$\pmb w \leftarrow \pmb w+y\pmb x$,直到所有样本分对。
根据感知机的学习策略,可以反推出,当样本分错时才会产生损失,即:
$$
\mathcal L(\pmb w;\pmb x,y) = max(0,-y\pmb w^\top\pmb x)
$$
当数据集是两类线性可分时,两类感知机更新权重的次数不超过一个常数$R^2\over r^2$,这个性质称之为感知机的收敛性。

证明过程可以通过放缩来确定第K次更新感知器的权重向量时的上界和下界,这里不再推导。
支持向量机(SVM)
支持向量机是这样的一种模型,它的目的在于寻找一个超平面$(\pmb w^*,b^*)$,使得间隔最大,即选择间隔最大的决策边界。
首先是求最短边界$\gamma$的一般方法:
那么,支持向量机的最大间隔的决策边界可以通过以下方式表示:
$$
\max_{w,b} \ \ \ \ \mathcal \gamma \\\\
s.t. \ \ \ \ {y^{n}(\pmb w^\top\pmb x^{n}+b) \over ||\pmb w||} \ge \gamma
$$
限制$||\pmb w||·\gamma = 1$,上式可以转写为
$$
\min_{w,b} \ \ \ \ \mathcal ||\pmb w|| \\\\
s.t. \ \ \ \ {y^{n}(\pmb w^\top\pmb x^{n}+b)} \ge 1,
$$
根据支持向量机的条件时,我们可以得知,获取决策边界时会以距离为$\pm$1为边界,判断其是否成功分类,因此就有了支持向量的概念。
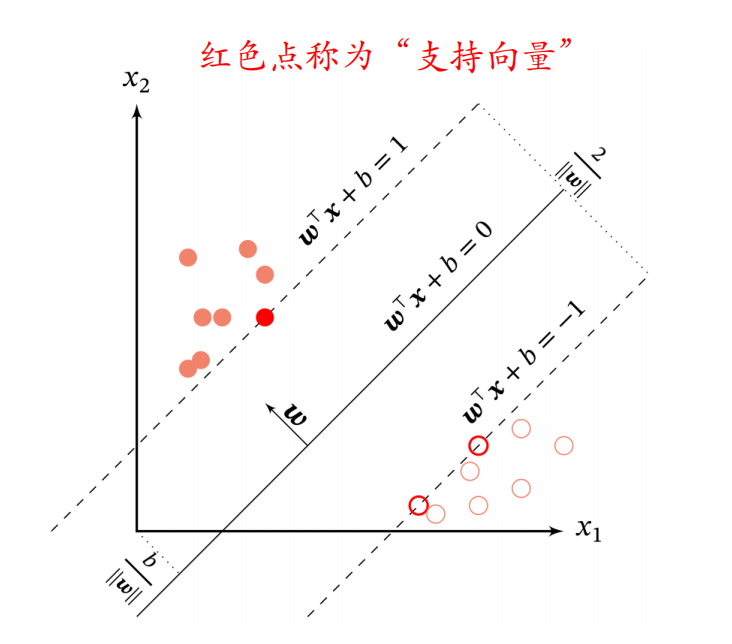
若训练集线性不可分,则SVM算法本身无法找到最优解,为了能够容忍部分不满足约束的样本,使SVM能够有更高的使用空间,引入松弛变量$\xi$

小结
