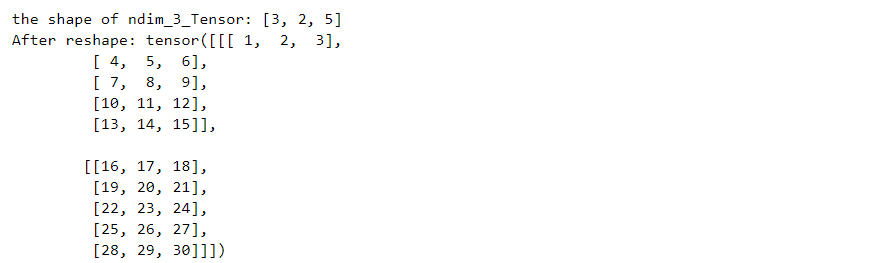神经网络与深度学习实验一——实验基础

本文最后更新于：几秒前

【注】

本实验及之后的实验都将从PaddlePaddle和Pytorch两个版本进行，其中paddlepaddle是邱锡鹏老师官方的实验工具，pytorch是我为了能尽快上手而尝试的工具（×）

实验文档的大部分文字都来源于邱锡鹏老师的网课练习notebook中，部分会进行补充或精简

本节实验介绍

本次实验是有关于实验基础知识的讲解，包括张量、算子和数据集等信息

  • 张量：深度学习中表示和存储数据的主要形式。
  • 算子：构建神经网络模型的基础组件。每个算子有前向和反向计算过程，前向计算对应一个数学函数，而反向计算对应这个数学函数的梯度计算。有了算子，我们就可以很方便地通过算子来搭建复杂的神经网络模型，而不需要手工计算梯度。

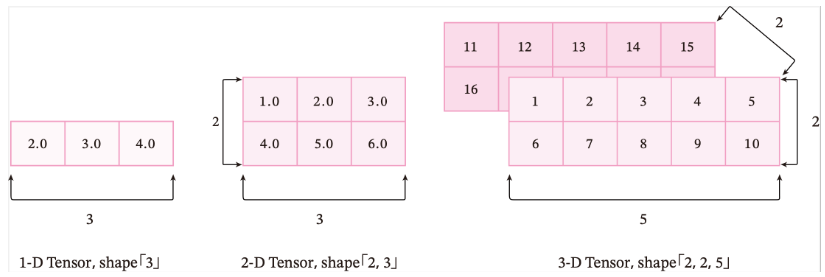
张量

在深度学习的实践中，我们通常使用向量或矩阵运算来提高计算效率。比如$w_1x_1 + w_2 x_2 +\cdots +w_N x_N$的计算可以用$w^\top x$来代替，这样可以充分利用计算机的并行计算能力，特别是利用GPU来实现高效矩阵运算。在深度学习中，以张量来存储与表示数据，张量是矩阵的扩展与延伸，可以认为是高阶的矩阵。1阶张量为向量，2阶张量为矩阵。如果你对Numpy熟悉，那么张量是类似于Numpy的多维数组(ndarray)的概念，可以具有任意多的维度。

image-20221012160709716

单个张量的数据类型必须是一致的，这个数据类型可以是布尔型、整型、复数等，因此需要给张量定义一个数据类型(dtype)来表示其数据类型。

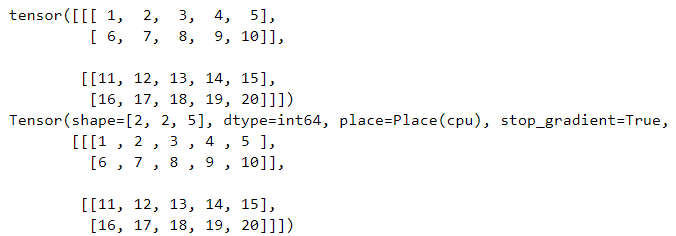
创建张量

1
2
3
4
5
6
7
8
9
10
11
# 创建多维Tensor
# paddlepaddle
ndim_n_Tensor = paddle.to_tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]]])
# pytorch
ndim_n_Tensor = torch.tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]]])

image-20221012212400850

需要注意的是，张量在任何一个维度上的元素数量必须相等。

指定形状（torch和paddle的API用法一致）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
m, n = 2, 3

# 使用zeros创建数据全为0，形状为[m, n]的Tensor
zeros_paddle = paddle.zeros([m, n])
zeros_torch = torch.zeros([m,n])
# 使用ones创建数据全为1，形状为[m, n]的Tensor
ones_paddle = paddle.ones([m, n])
ones_torch = torch.ones([m,n])
# 使用full创建数据全为指定值，形状为[m, n]的Tensor，这里我们指定数据为10
full_paddle = paddle.full([m, n], 10)
full_torch = torch.full([m,n],10)
# 使用arange创建以步长step均匀分隔数值区间[start, end)的一维Tensor
arange_paddle = paddle.arange(start=1, end=5, step=1)
arrage_torch = torch.arange(start=0, end, step=1)
# 使用linspace创建以元素个数num均匀分隔数值区间[start, stop]的Tensor
linspace_paddle = paddle.linspace(start=1, stop=5, num=5)
linspace_torch = torch.linspace(start=0, end=10, step=2)

张量有如下属性：

  • ndim：张量的维度，例如向量的维度为1，矩阵的维度为2。
  • shape： 张量每个维度上元素的数量。
  • shape[n]：张量第nn维的大小。第nn维也称为轴（axis）。
  • size：张量中全部元素的个数。

以torch的张量属性为例，paddle与torch不同的用法另外标注：

1
2
3
4
5
6
7
8
9
10
ndim_4_Tensor = torch.ones([2, 3, 4, 5])
ndim_4_p = paddle.ones([2,3,4,5])
print("Number of dimensions:", ndim_4_Tensor.ndim)
print("Shape of Tensor:", ndim_4_Tensor.shape)
print("Elements number along axis 0 of Tensor:", ndim_4_Tensor.shape[0])
print("Elements number along the last axis of Tensor:", ndim_4_Tensor.shape[-1])
#torch:numel()函数计算元素数量
print('Number of elements in Torch tensor: ', ndim_4_Tensor.numel())
#paddle:size属性计算元素数量
print("Number of elements in Paddle tensor: ", ndim_4_p.size)

image-20221012235143510

张量的形状也可以通过reshape函数来进行变换，变换后数据本身和数据的相对顺序都不会有变化。

1
2
3
4
5
6
7
8
9
#paddle用法一致
ndim_3_Torch = torch.tensor([[[1, 2, 3, 4, 5],
                                   [6, 7, 8, 9, 10]],
                                  [[11, 12, 13, 14, 15],
                                   [16, 17, 18, 19, 20]],
                                  [[21, 22, 23, 24, 25],
                                   [26, 27, 28, 29, 30]]])
reshape_torch = torch.reshape(ndim_3_Torch,[2, 5, 3])
print("After reshape:", reshape_Tensor)

image-20221013001623336

注意这里的修改前和修改后的shape_size应该是一样的，否则会报错

image-20221013001934299

使用reshape时有一些简单技巧：

  1. reshape中有且仅有一维可以为-1，表示按照原有size直接补齐
  2. reshape中可以有多维为0，表示继承原有张量在当前维度的元素个数

除了reshape变换外，还可以使用unsqueeze函数在原有张量基础上插入尺寸为1的维度，其中paddlepaddle支持多个维度的插入，而pytorch的dim参数为整型，限制只能有一个维度的插入。

1
2
3
4
5
6
7
8
ones_Torch = torch.ones([5, 10])
new_Torch1 = torch.unsqueeze(ones_Tensor, 0)
print('new Tensor 1 shape: ', new_Tensor1.shape)
new_Torch2 = torch.unsqueeze(ones_Tensor, 2)
print('new Tensor 2 shape: ', new_Tensor2.shape)
ones_Paddle = paddle.ones([5,10])
new_Paddle1 = paddle.unsqueeze(ones_Paddle,[1,2])
print('new Tensor 3 shape: ',new_Paddle1.shape)

image-20221013003536929

数据类型

dtype参数用来查看张量的数据类型，支持类型支持bool、float16、float32、float64、uint8、int8、int16、int32、int64和复数类型等数据。其中通过Python元素创建的数据可以使用dtype指定类型，默认整型为int64，浮点类型为float32；通过Numpy数组创建的张量，则与其原来的数据类型保持相同。

paddle的to_tensor函数和torch的as_tensor函数可以实现从其他类型（包括Numpy）到tensor的转换

1
2
3
# 使用paddle.to_tensor通过已知数据来创建一个Tensor
print("Tensor dtype from Python integers:", torch.as_tensor(1).dtype)
print("Tensor dtype from Python floating point:", paddle.to_tensor(1.0).dtype)

如果想要修改数据类型，paddle使用cast函数，torch使用to方法可以实现。

1
2
3
4
5
6
7
8
9
10
# 定义dtype为float32的Tensor
float32_Tensor_Torch = torch.as_tensor(1.0)
float32_Tensor_Paddle = paddle.to_tensor(1.0)
# paddle.cast和torch的to可以将输入数据的数据类型转换为指定的dtype并输出。支持输出和输入数据类型相同。
# 注意两者的使用区别
int64_Tensor_Paddle = paddle.cast(float32_Tensor_Paddle,dtype='int64')
int64_Tensor_Torch = float32_Tensor_Torch.to(torch.int64)

print("Tensor after cast to int64:", int64_Tensor_Paddle.dtype,int64_Tensor_Torch.dtype)

image-20221013152808890

设备转换

在paddle中共有三种可使用的设备类型，使用place参数进行设置

1
2
3
4
5
6
7
8
9
10
# 创建CPU上的Tensor
cpu_Tensor = paddle.to_tensor(1, place=paddle.CPUPlace())
# 通过Tensor.place查看张量所在设备位置
print('cpu Tensor: ', cpu_Tensor.place)
# 创建GPU上的Tensor
gpu_Tensor = paddle.to_tensor(1, place=paddle.CUDAPlace(0))
print('gpu Tensor: ', gpu_Tensor.place)
# 创建固定内存上的Tensor，固定内存的读写效率会更高，但存储空间的消耗也会更多
pin_memory_Tensor = paddle.to_tensor(1, place=paddle.CUDAPinnedPlace())
print('pin memory Tensor: ', pin_memory_Tensor.place)

在torch中需要使用device方法设置具体的设备对象，torch.device()方法是在torch中使用频率十分高的一种方法。torch.device代表将torch.tensor分配到的设备的对象。torch.device可以采用字符串和编号的参数定义设备

1
2
3
4
5
6
7
8
#字符串方法
torch.device('cuda:0')
torch.device('cpu')
torch.device('cuda')  # current cuda device
#字符串+编号方法
#0号显卡
torch.device('cuda', 0)
torch.device('cpu', 0)

访问张量

paddle和torch都支持python和Numpy的索引和切片操作

1
2
3
4
5
6
7
8
9
10
11
12
# torch.as_tensor定义1个一维Tensor
ndim_1_Tensor = torch.as_tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])
# paddle.to_tensor定义1个一维Tensor
ndim_1_Tensor = paddle.to	_tensor([0, 1, 2, 3, 4, 5, 6, 7, 8])

print("Origin Tensor:", ndim_1_Tensor)
print("First element:", ndim_1_Tensor[0])
print("Last element:", ndim_1_Tensor[-1])
print("All element:", ndim_1_Tensor[:])
print("Before 3:", ndim_1_Tensor[:3])
print("Interval of 3:", ndim_1_Tensor[::3])
print("Reverse:", ndim_1_Tensor[::-1])

二维的张量同样可以采用索引或切片访问与修改，其中每个参数对应其中的一维。以torch为例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#%% torch为例，paddle和torch的操作一致
# 定义1个二维Tensor
ndim_2_Tensor = torch.as_tensor([[0, 1, 2, 3],
                                  [4, 5, 6, 7],
                                  [8, 9, 10, 11]])
print("Origin Tensor:", ndim_2_Tensor)
print("First row:", ndim_2_Tensor[0])
print("First row:", ndim_2_Tensor[0, :])
print("First column:", ndim_2_Tensor[:, 0])
print("Last column:", ndim_2_Tensor[:, -1])
print("All element:", ndim_2_Tensor[:])
print("First row and second column:", ndim_2_Tensor[0, 1])

ndim_2_Tensor[0:2,2:] = 100
print("After Change: ",ndim_2_Tensor)

image-20221014143213976

【提醒】慎重通过索引或切片操作来修改张量，此操作仅会原地修改该张量的数值，且原值不会被保存。如果被修改的张量参与梯度计算，将仅会使用修改后的数值，这可能会给梯度计算引入风险。

张量运算

在这里我们更加推荐使用数学函数进行计算，这里给出比较常用的运算函数，更多请见pytorch-Tensor操作文档和Paddle官方文档

数值计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#加减乘除运算
x.add(y)         		      # 逐元素加
x.subtract(y)       		  # 逐元素减
x.multiply(y)       		  # 逐元素乘（积）
x.divide(y)         		  # 逐元素除
x.mod(y)            		  # 逐元素除并取余
x.pow(y)            		  # 逐元素幂
#取整与约分
x.abs()                       # 逐元素取绝对值
x.ceil()                      # 逐元素向上取整
x.floor()                     # 逐元素向下取整
x.round()                     # 逐元素四舍五入
#计算函数
x.exp()                       # 逐元素计算自然常数为底的指数
x.log()                       # 逐元素计算x的自然对数
x.reciprocal()                # 逐元素求倒数
x.square()                    # 逐元素计算平方
x.sqrt()                      # 逐元素计算平方根
x.sin()                       # 逐元素计算正弦
x.cos()                       # 逐元素计算余弦
#求和与比较
x.max()                       # 指定维度上元素最大值，默认为全部维度
x.min()                       # 指定维度上元素最小值，默认为全部维度
x.prod()                      # 指定维度上元素累乘，默认为全部维度
x.sum()    					  # 指定维度上元素的和，默认为全部维度

逻辑计算

1
2
3
4
5
6
7
8
x.isfinite()                  # 判断Tensor中元素是否是有限的数字，即不包括inf与nan
x.equal(y)                    # 判断两个Tensor的每个元素是否相等，并返回形状相同的布尔类Tensor
x.not_equal(y)                # 判断两个Tensor的每个元素是否不相等
x.less(y)                # 判断Tensor x的元素是否小于Tensor y的对应元素
x.less_equal(y)               # 判断Tensor x的元素是否小于或等于Tensor y的对应元素
x.greater(y)             # 判断Tensor x的元素是否大于Tensor y的对应元素
x.greater_equal(y)            # 判断Tensor x的元素是否大于或等于Tensor y的对应元素
x.allclose(y)                 # 判断两个Tensor的全部元素是否接近

矩阵运算

1
2
3
4
5
x.t()                         # 矩阵转置
x.transpose(1, 0)           # 交换第 0 维与第 1 维的顺序
x.norm('fro')                 # 矩阵的弗罗贝尼乌斯范数
x.dist(y, p=2)                # 矩阵（x-y）的2范数
x.matmul(y)                   # 矩阵乘法

广播

pytorch和paddle中都支持使用广播机制对两个维度不同的矩阵进行计算，属于数组的广播机制。通常来讲，如果有一个形状较小和一个形状较大的张量，会希望多次使用较小的张量来对较大的张量执行某些操作，看起来像是形状较小的张量首先被扩展到和较大的张量形状一致，然后再做运算。

广播的规则：

  1. 每个张量至少为一维
  2. 从后往前比较张量的形状，当前维度的大小要么相等，要么其中一个等于1，要么其中一个不存在。

广播的计算规则：

  1. 如果两个张量shape的长度不一致，那么需要在较小长度的shape前添加1，直到两个张量的形状长度相等
  2. 保证两个张量形状相等之后，每个维度上的结果维度就是当前维度上较大的那个。

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 当两个Tensor的形状一致时，可以广播
x = torch.ones((2, 3, 4))
y = torch.ones((2, 3, 4))
z = x + y
print('broadcasting with two same shape tensor: ', z.shape)

x = torch.ones((2, 3, 1, 5))
y = torch.ones((3, 4, 1))
'''首先补足y = shape(1,3,4,1)
		 x = shape(2,3,1,5)
   按位进行合并，对应位上或者相等，或者有一位为1可以直接合并
   1 cpr 2 --> 2
   3 cpr 3 --> 3
   4 cpr 1 --> 4
   1 cpr 5 --> 5
'''
z = x + y
#z = shape(2,3,4,5)
print('broadcasting with two different shape tensor:', z.shape)

矩阵乘法matmul中也用到了广播的机制，其将矩阵看作一个对象单位，和数据广播的数值处在同一等级，然后进行广播计算，具体的

  • 如果两个张量均为一维，则获得点积结果。
  • 如果两个张量都是二维的，则获得矩阵与矩阵的乘积。
  • 如果张量x是一维，y是二维，则将x的shape前面补一维变成[1, D]，与y进行矩阵相乘后再删除前置尺寸。
  • 如果张量x是二维，y是一维，则获得矩阵与向量的乘积。
  • 如果两个张量都是N维张量（N > 2），则根据广播规则广播非矩阵维度（除最后两个维度外其余维度）。比如：如果输入x是形状为[j,1,n,m]的张量，另一个y是[k,m,p]的张量，则输出张量的形状为[j,k,n,p]。

原位操作

在torch和paddle中，计算函数的返回结果都是创一个新的张量来存储，而不会形象原有的张量，这种处理方式称为”非原位“，部分函数支持通过在函数后加一个下划线来实现原位操作，如x.add(y) –> x.add_(y)

算子

基于深度学习的前向传播与反向传播两个流程，从$x$到$y$的计算看作一个前向计算过程。前向的传播流程$y=f_L(\cdots f_2(f_1(x)))$，则$f_l(⋅)$称为前向函数；而神经网络的参数学习需要找到函数对所有参数的偏导数。

依据链式法则：$\begin{aligned}\frac{\partial y}{\partial \theta_l} &= {\frac{\partial f_l}{\partial \theta_l}} \frac{\partial y}{\partial f_l} \&= \frac{\partial f_l}{\partial \theta_l} \frac{\partial f_{l+1}}{\partial f_l} \cdots \frac{\partial f_L}{\partial f_{L-1}} .\end{aligned}$，一种比较高效的方法就是递归计算每个偏导，反向计算。令$\delta_l\triangleq \frac{\partial y}{\partial f_l}$，则有$\delta_{l-1} = \frac{\partial f_l}{\partial f_{l-1}} \delta_{l}.$，则从后往前可以计算出所有的偏导。

如果我们实现每个基础函数的前向函数和反向函数，就可以非常方便地通过这些基础函数组合出复杂函数，并通过链式法则反向计算复杂函数的偏导数。 在深度学习框架中，这些基本函数的实现称为算子(Operator，Op)。有了算子，就可以像搭积木一样构建复杂的模型。

算子定义

算子是构建复杂机器学习模型的基础组件，包含一个函数$f(x)$的前向函数和反向函数。为了可以更便捷地进行算子组合，

本书中定义算子Op的接口如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(inputs)

    # 前向函数
    # 输入：张量inputs
    # 输出：张量outputs
    def forward(self, inputs):
        # return outputs
        raise NotImplementedError

    # 反向函数
    # 输入：最终输出对outputs的梯度outputs_grads
    # 输出：最终输出对inputs的梯度inputs_grads
    def backward(self, outputs_grads):
        # return inputs_grads
        raise NotImplementedError

算子应用

以$g = \exp(a \times b+c \times d)$为例，分别实现加法、乘法和指数运算三个算子，通过算子组合计算$y$值。

加法算子

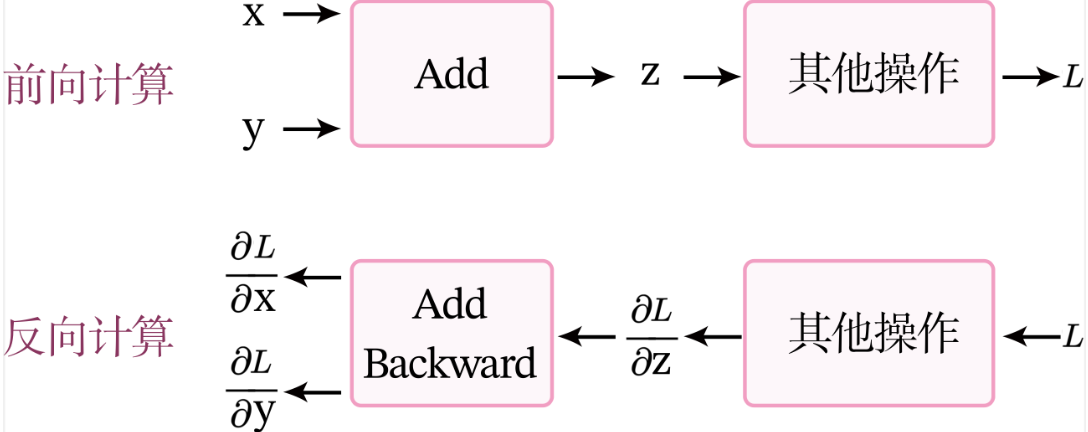
加法算子的计算过程如下：

image-20221015180158188

前向计算的过程输出的是x+y=z，即输出z做结果；反向计算梯度，假设输出的结果为L，最终输出为$L$，令$\delta_z=\frac{\partial L}{\partial z}$，$\delta_x=\frac{\partial L}{\partial x}$，$\delta_y=\frac{\partial L}{\partial y}$。加法算子的反向计算的输入是梯度$\delta_z$，输出是梯度$\delta_x$和$\delta_y$。根据链式法则，$\delta_y=\frac{\partial z}{\partial y}\delta_z$，可以直接根据z = x+y求得$\delta_x = \delta_z \times 1$，$\delta_y = \delta_z \times 1$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class add(Op):
    def __init__(self):
        super(add, self).__init__()
	#调用add函数时默认调用前向过程
    def __call__(self, x, y):
        return self.forward(x, y)
	#前向过程
    def forward(self, x, y):
        self.x = x
        self.y = y
        outputs = x + y
        return outputs
	#反向过程
    def backward(self, grads):
        grads_x = grads * 1
        grads_y = grads * 1
        return grads_x, grads_y

乘法算子

同加法算子的原理，前向传播计算乘法的结果，反向传播计算梯度，根据z = x*y求得$\delta_x = \delta_z \times y$，$\delta_y = \delta_z \times x$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class multiply(Op):
    def __init__(self):
        super(multiply, self).__init__()

    def __call__(self, x, y):
        return self.forward(x, y)

    def forward(self, x, y):
        self.x = x
        self.y = y
        outputs = x * y
        return outputs

    def backward(self, grads):
        grads_x = grads * self.y
        grads_y = grads * self.x
        return grads_x, grads_y

指数算子

输入x，前向传播计算指数函数$z=e^x$，反向传播计算梯度，根据公式可得$\delta_x = \delta_z \times e^x$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import math

class exponential(Op):
    def __init__(self):
        super(exponential, self).__init__()

    def forward(self, x):
        self.x = x
        outputs = math.exp(x)
        return outputs

    def backward(self, grads):
        grads = grads * math.exp(self.x)
        return grads

对算子进行结合应用

1
2
3
4
5
6
7
8
9
10
11
12
13
a, b, c, d = 2, 3, 2, 2
# 实例化算子
multiply_op = multiply()
add_op = add()
exp_op = exponential()
y = exp_op(add_op(multiply_op(a, b), multiply_op(c, d)))
print('y: ', y)

z = exp_op.backward(z)
x,y = add_op.backward(z)
x1,y1 = multiply_op.backward(x)
x2,y2 = multiply_op.backward(y)
print(x1," ",y1," ",x2," ",y2)

自动微分机制

目前大部分深度学习平台都支持自动微分（Automatic Differentiation），即根据forward()函数来自动构建backward()函数。自动微分的原理是将所有的数值计算都分解为基本的原子操作，并构建计算图DAG（可以理解为有向无环图）。在模型的构建阶段实时生成有关过程的图。

img

预定义算子

在深度学习中，大多数模型都是以各种神经网络为主，由一系列层(Layer)组成，层是模型的基础逻辑执行单元。如paddle.nn.Layer、torch.nn.Layer类来方便快速地实现自己的层和模型。当我们实现的算子继承Layer类时，就不用再定义backward函数，自动微分机制可以自动完成反向传播过程，让我们只关注模型构建的前向过程，不必再进行烦琐的梯度求导。

完

学习笔记
#神经网络与深度学习
神经网络与深度学习实验一——实验基础
http://paopao0226.site/post/37103f0b.html
作者
Ywj226
发布于
2022年10月14日
更新于
2023年9月23日
许可协议