机器学习概述笔记

《神经网络与机器学习》第二章笔记

概述

机器学习的三要素

模型、学习准则、优化

线性回归

模型：$f(\boldsymbol{x} ; \boldsymbol{w},b)=\boldsymbol{w}^{\top} \boldsymbol{x}+b$，使用增广矩阵表示

概率基础

伯努利分布

在一次试验中，事件A出现的概率为$µ$，不出现的概率为$1 − µ$。若用变量X表示事件A出现的次数，则X的取值为0和1，其相应的分布为
$$
P(X)=μ^{X}(1-μ)^{1-X}
$$

二项分布

在n次伯努利分布中，若以变量X表示事件A出现的次数，则X 的取值为{0,… ,n}
$$
P(x=k)=C^k_ nμ^{k}(1-μ)^{1-k}
$$

累计随机变量(CDF)

$$
cdf(x) = \begin{cases}
P(X \le x) & \text{if X是离散随机变量} \\[2ex]
\int^x_ {-\infty} & \text{if X是连续变量} \\
\end{cases}
$$

条件概率

对于离散随机向量$(X,Y)$，已知$X = x$的条件下，随机变量$Y = y$的条件概率为：
$$
p(y|x) = P(Y=y|X=x) = {p(x,y) \over p(x)}
$$

贝叶斯公式

两个条件概率 $p(y|x)$ 和 $p(x|y)$ 之间的关系
$$
p(y|x)={p(x|y)p(y) \over p(x)}
$$

期望

随机变量的均值
$$
\mathbb E[X] =
\begin{cases}
\sum^N_ {n=1}{x_ np(x_ n)} \\[2em]
\int_\mathbb R xp(x) dx
\end{cases}
$$

大数定律

当样本足够大时，样本的均值将无限接近于分布期望

最大似然与最大后验

根据贝叶斯公式$p(w|x) = {p(x|w)p(w) \over p(x)}$得
$$
p(w|x) \propto p(x|w)p(w)
$$
其中，我们称$p(x|w)$是基于先验的似然函数，$p(w)$是先验，$p(w|x)$是后验函数，即：
$$
后验(posterior) \propto 似然(likelihood) \times 先验(prior)
$$
似然函数是关于统计模型$p(x;w)$的参数w的函数，和概率$p(x;w)$的表示方法一致，但看待角度不同，概率$p(x;w)$是描述固定参数$w$后，随机变量$x$的分布情况，是对$x$的看待角度；似然$p(x;w)$则是描述已知随机变量$x$时，不同参数$w$对分布产生的影响，是对$w$的看法。

一般我们看到的是这样的表示形式
$$
p(w|X,y;\nu,\sigma) \propto p(y|X,w;\sigma) \times p(w,\nu), (2.1)
$$
最大似然估计是找到一组参数$w$使得似然函数$p(y|X,w;\sigma)$最大，即
$$
MLE=\arg\max_w\ p(y|X,w;\sigma)=\arg\max_w\ log(p(y|X,w;\sigma))
$$
令${\partial logp(y|X,w;\sigma) \over \partial w} = 0$，可得$w^{ML}=(XX^\top)^{-1}Xy$（计算略）。

后验是对似然与先验的综合考量，更多的，最大后验估计是找到一组$w$使得后验函数$p(w|X,y;\nu,\sigma)$最大，即有
$$
MAP=\arg\max_w\ p(w|X,y;\nu,\sigma)
\propto \arg\max_w\ p(y|X,w;\sigma) \times p(w,\nu) \\
= \arg\max_w\ log(p(y|X,w;\sigma) \times p(w,\nu))
= \arg\max_w\ log(p(y|X,w;\sigma))+ \arg\max_w\ p(w,\nu)\\
= MLE+||w||
$$
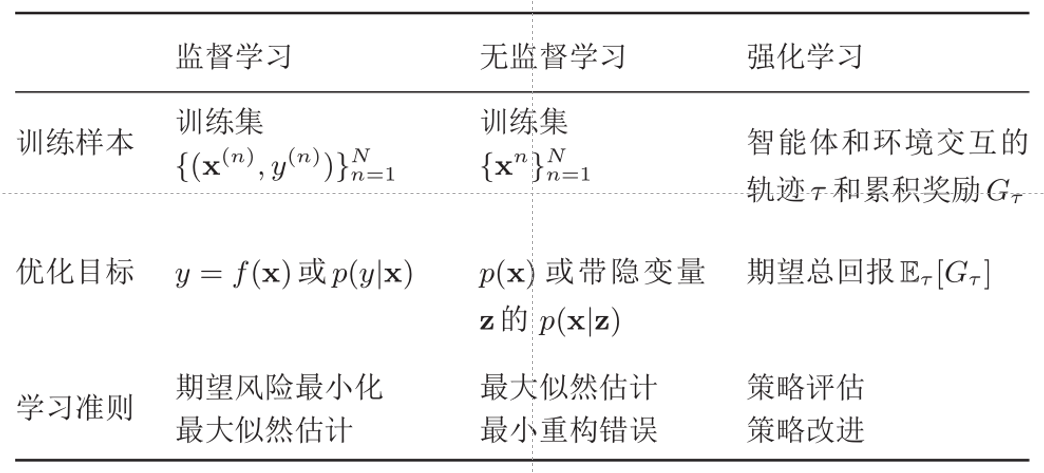
可知，MAP就是在MLE的基础上加入了正则化惩罚项。更多的，我们可以得出以下表格（计算略）

几个关键点

常见的机器学习类型包括监督学习、无监督学习与强化学习三种

模型选择问题——验证集

引入验证集，将训练集按照7:3或者8:2的比例分成训练集和验证集，其中验证集用于选择在验证集上表现最好的模型。

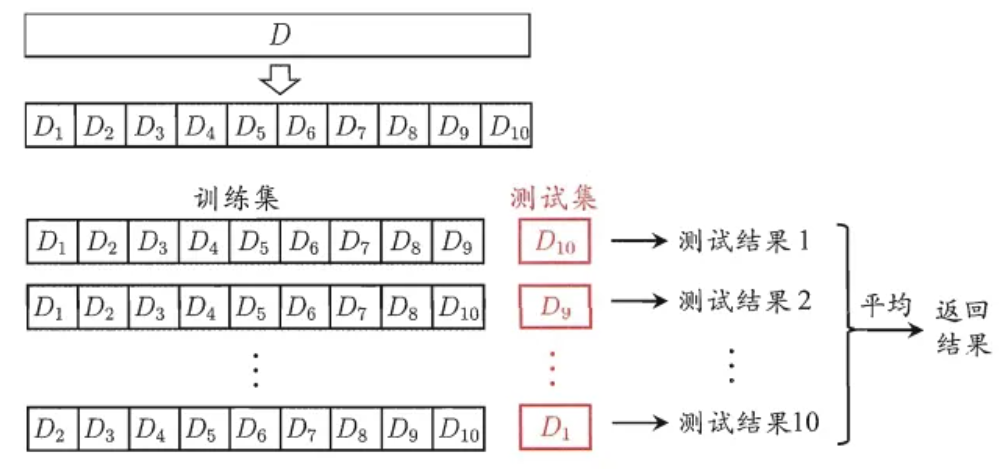
数据稀疏问题——交叉验证

将训练集分成S组，每次使用S-1组作为训练集，剩下的一组作为验证集，选择在验证集上平均性能最好的一组。

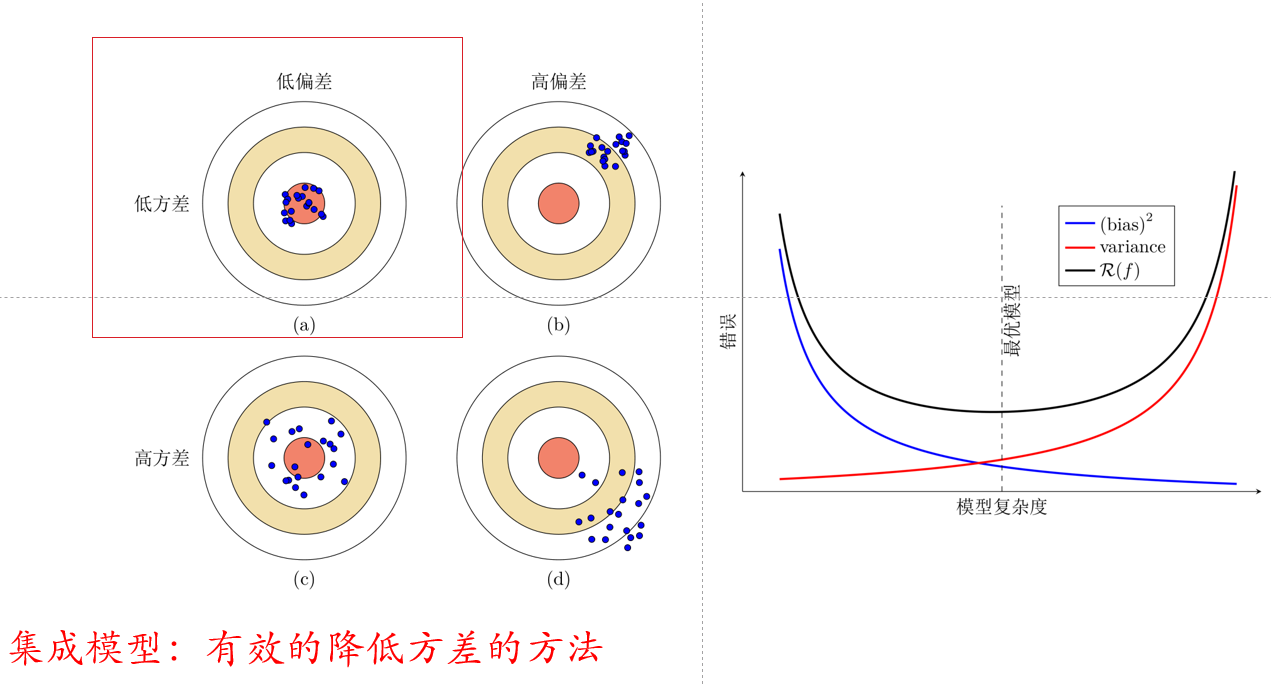
期望风险中的偏差与方差求解

偏差与方差都是在模型中需要去考虑和中和的点。

PAC学习

根据大数定律，当训练集大小$|D|$趋向无穷大时，泛化错误趋向于0，即经验风险趋近于期望风险。

PAC学习的表达式如下：
$$
P((\mathcal R(\mathcal f) - \mathcal R^{emp}_\mathcal D(f)) \le \epsilon) \ge 1-\delta
$$
其中，$(\mathcal R(\mathcal f) - \mathcal R^{emp}_\mathcal D(f)) \le \epsilon$表示经验误差与结构误差需近似正确，$\epsilon \in (0,0.5)$；$P(…)\ge 1 - \delta $ 表示可能性，$\delta \in (0,0.5)$。如果固定$\epsilon和\delta$，可以反过来计算出样本的复杂度为（计算略）
$$
n(\epsilon,\delta) \ge {1 \over 2\epsilon^2}(ln|\mathcal F|+ln{2\over\delta})
$$
公式表明，如果希望模型的假设空间$|\mathcal F|$越大，泛化误差越小，那么其需要的样本数量$n$也就越多。

常见定理

天下没有午餐定理

对于基于迭代的最优化算法，不存在某种算法对所有问题（有限的搜索空间内）都有效。如果一个算法对某些问题有效，那么它一定在另外一些问题上比纯随机搜索算法更差。

丑小鸭定理

丑小鸭与白天鹅之间的区别和两只白天鹅之间的区别一样大，即特征差别一样大。比较时需要确定比较标准。

奥卡姆剃刀原理

在效力相同情况下，简单的模型要优于更为复杂的模型

归纳偏置

很多学习算法经常会对学习的问题做一些假设，这些假设就称为归纳偏置，归纳偏置在贝叶斯学习中也经常称为先验（Prior）。

索引->B树