卷积神经网络笔记
本文最后更新于:几秒前
《神经网络与机器学习》第五章笔记
前提
- 全连接神经网络的权重矩阵参数非常多,容易受到干扰。
- 自然图像中的物体都具有局部不变性特征。
卷积神经网络的特性
- 局部连接
- 权重共享(卷积核)
- 空间或时间上的次采样
卷积
概念
卷积经常用在信号处理的过程中,用于计算信号的延迟累积
假设信号发生器每个时刻$t$产生一个信号$x_t$,信号的衰减系数分别为$[w_1,w_2,…,w_K]$,则有收到的信号$y_t$为
$$
y_t = \displaystyle \sum_{k=1} ^K w_k x_{t-k+1}
$$
注意是,衰减系数$w$和信号$x$的下标是逆序的,这样,通过$K$个衰减系数可知,下一层的参数只与上一层的$K$个参数相关,这个过程大大降低了参数的量。
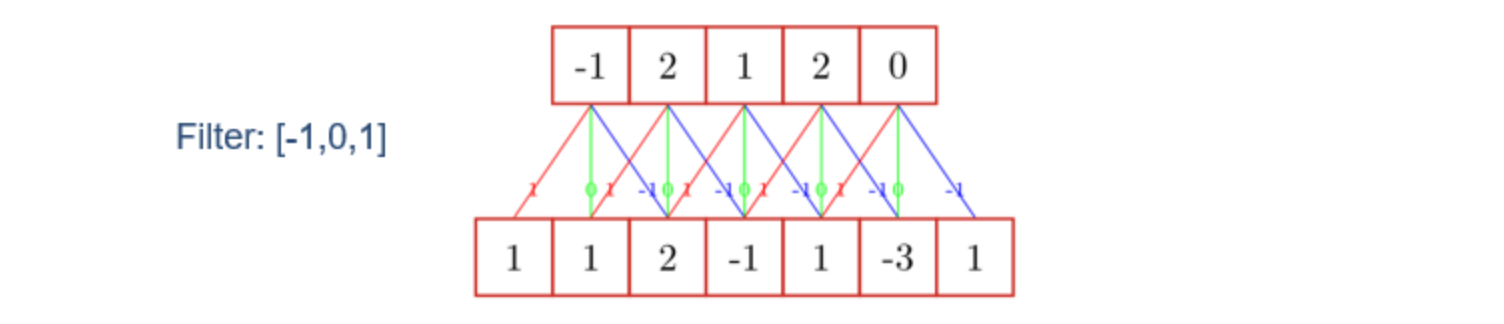
特定卷积核/特定滤波器
在这个问题中,衰减系数$w$又可以叫做卷积核或滤波器,其中,对于滤波器的不同值,其也有不同的作用
滤波器和作用的对应关系如下:
$w = [{1\over 2}, 0, -{1 \over 2}]$,近似于信号序列的一阶微分。
$x^ \prime (t) = {x(t+1) - x(t-1) \over 2}$
$w = [1,-2,1]$,近似于信号序列的二阶微分,二阶微分及更为高阶的微分可以用于提取高频信息(高频变化信号)。
$x^{\prime \prime}(t)={x^ \prime(t+1) - x ^\prime (t-1) \over 2}$
$w=[{1\over 3},{1\over 3},{1\over 3}]$,均值信号,可以用于提取信号的低频信息(低频变化信号)。
步长S与零填充P
进一步的,引入滤波器的滑动步长$S$和零填充$P$。
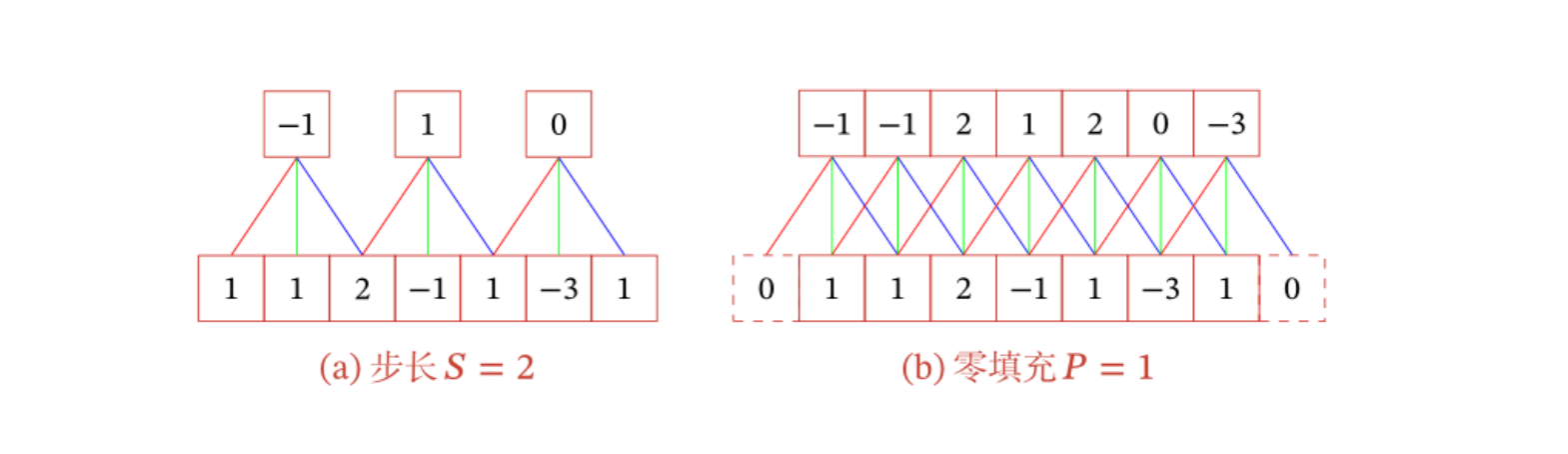
卷积类型(K为卷积核size)
- 窄卷积:步长$S=1$,零填充$P=0$,卷积后输出长度$L=M-K+1$
- 宽卷积:步长$S=1$,零填充$P = K-1$,卷积后输出长度$L=M-K+1+2\times(K-1) = M +K -1$
- 等宽卷积:步长$S=1$,零填充$P = (K-1)/2$,卷积后输出长度$L = M$
早期的文献中,卷积一般默认为窄卷积;目前的文献中,卷积一般都认为是等宽卷积
互相关
计算卷积的过程中,由于下标逆序,因此需要进行卷积核翻转,但卷积操作目标的本质是提取特征,这个过程与卷积核是否翻转没有关系,因此可以直接使用互相关代替卷积核
$$
y_{ij} = \sum_{u=1} ^m \sum_ {v=1} ^n w_ {uv} ·x_ {i+u-1,j+v-1}
$$
二维卷积

多个卷积核
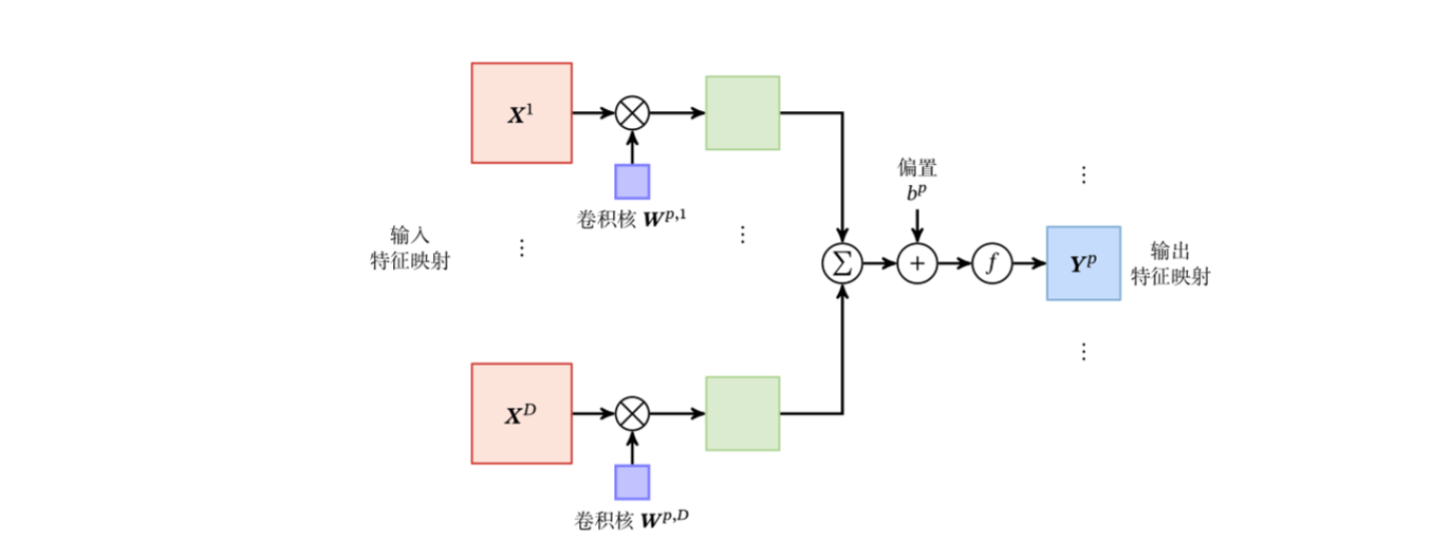
多个卷积核可以作为平行的单位进行卷积,每个卷积核可以卷积多次,因此输入和输出的第三维度可以有所不同。
$$
\begin{align}
\pmb Z^p & = \pmb W^p \otimes \pmb X + b^p = \sum_{d=1} ^D \pmb W^{p,d} \otimes \pmb X^d + b^p, \\\
Y^p & = f(\pmb Z^p)
\end{align}
$$
池化/汇聚
卷积层虽然可以显著减少连接的个数,但每个特征映射的神经元个数并没有显著减少,为了进一步减少卷积后的特征维度,可以采用池化的方法,通过一定策略进行缩小。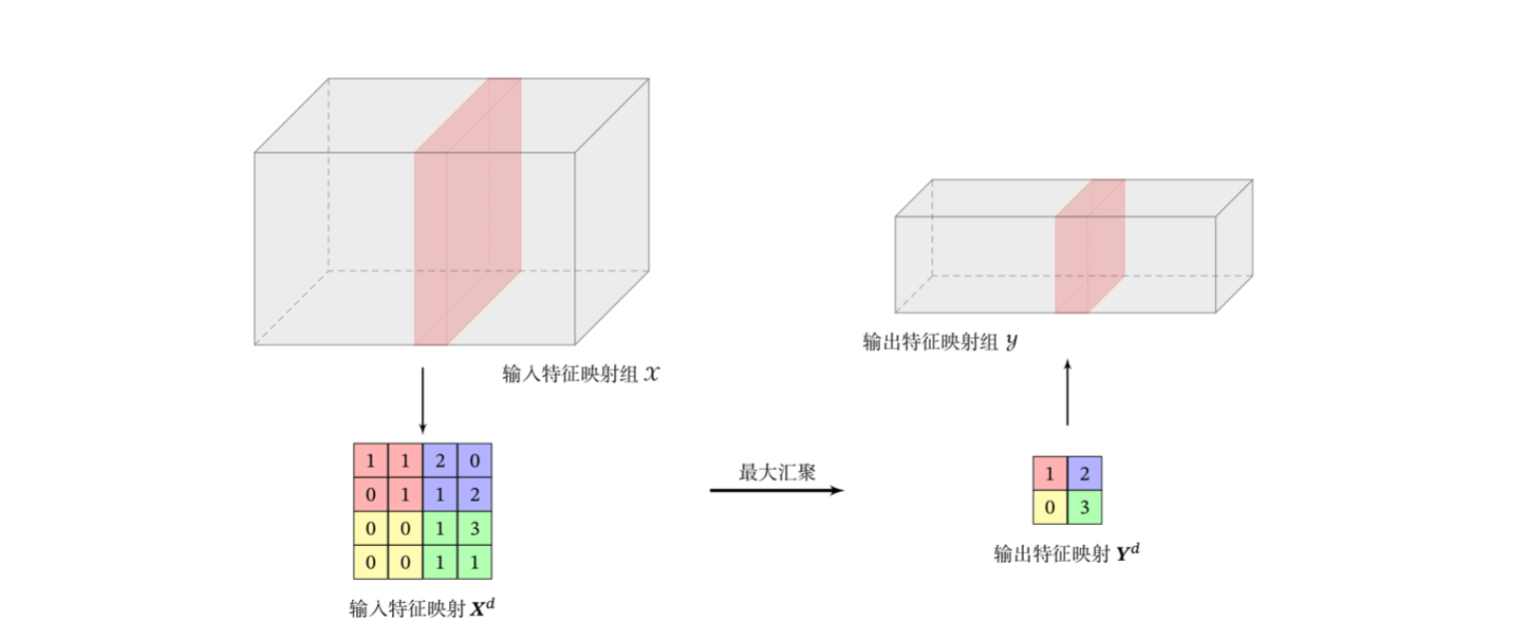
卷积网络的结构
典型结构

池化层/汇聚层其实可以看作是一种stride为K,卷积策略特殊的卷积层;一个卷积块为连续的$M$个卷积层和$b$个汇聚层(M通常设置为2-5,b为0或1)。一个卷积网络中可以堆叠$N$个连续的卷积块,然后再接着$K$个全连接层($N$的取值区间比较大,比如1-100或者更大;$K$一般为0~2)。
其他卷积种类
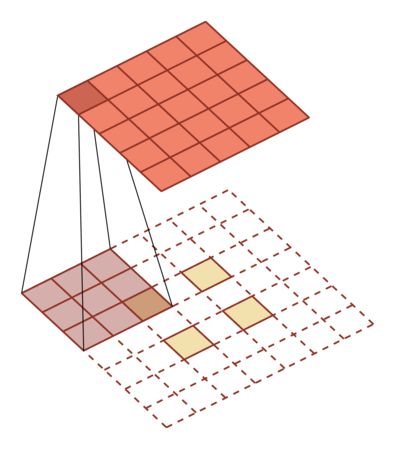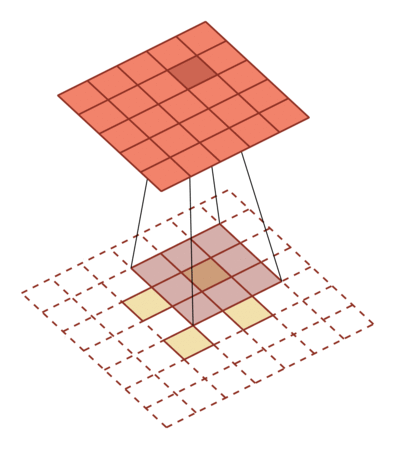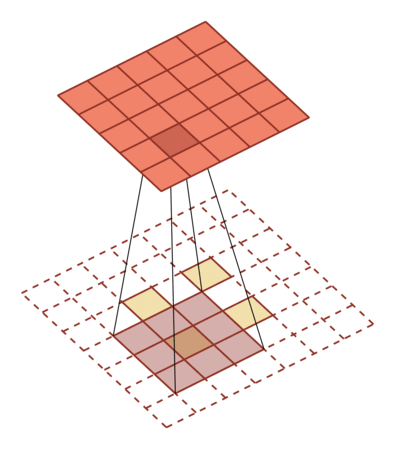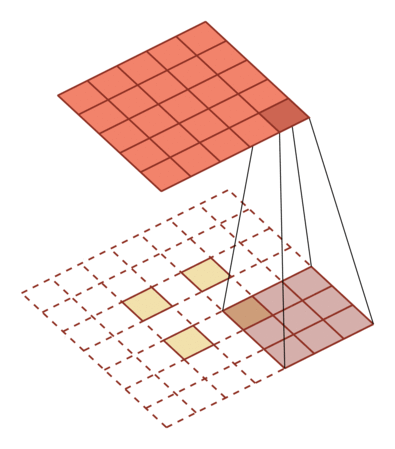
转置卷积/微步卷积
中间补充空洞(0),之前只需要走一步现在需要走两步,因此可以看作$stride = {1\over2}$
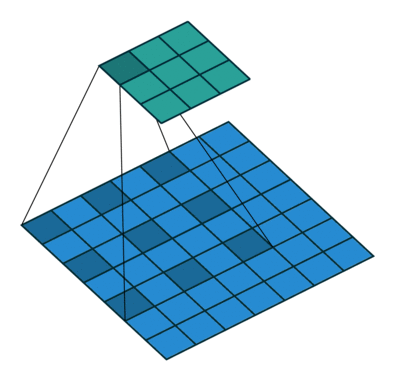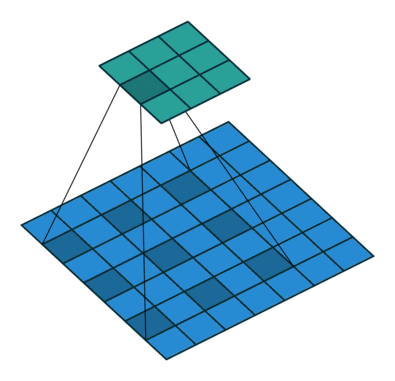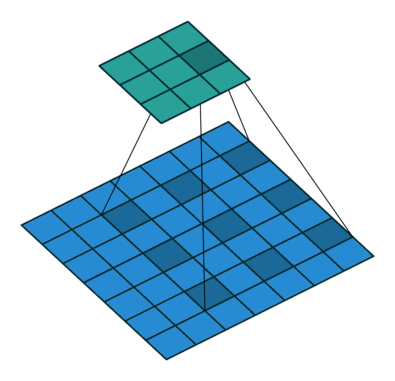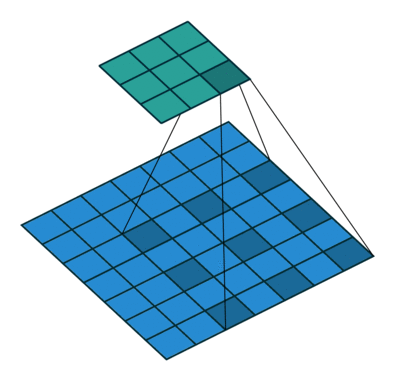
空洞卷积
空洞卷积可以通过给卷积核插入”空洞“来变相增加其大小,从而提高输出单元的感受野
典型卷积网络
LeNet-5
最早的成功在业界进行应用的神经网络模型,用于手写数字识别,共有七层。
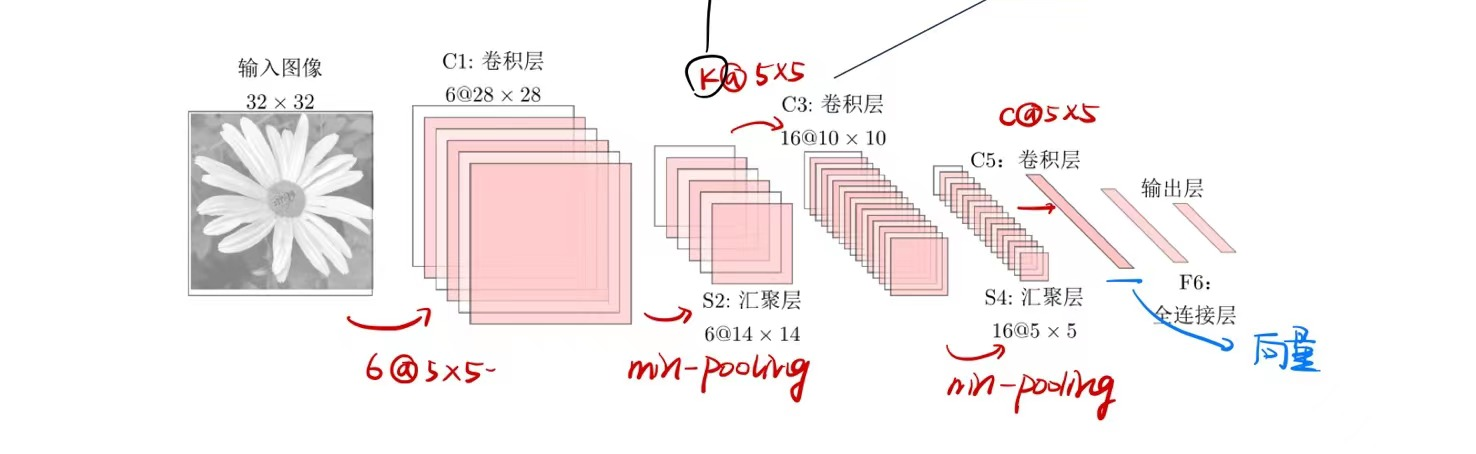
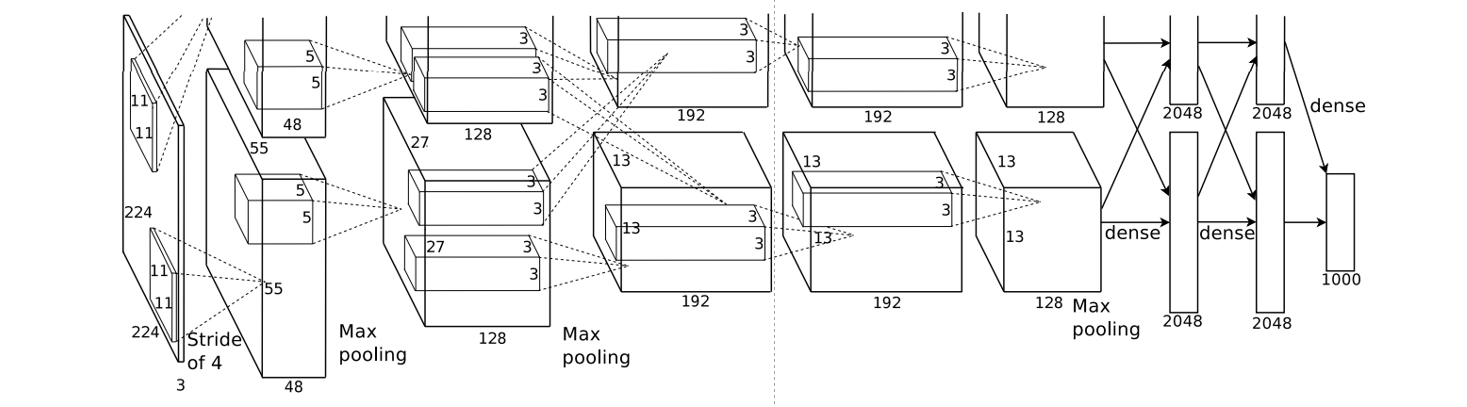
AlexNet
2012 ILSVRC winner
第一个现代深度卷积网络模型,采用了五个卷积层、三个池化层和两个全连接层,分成两路来降低显卡的显存要求。
Inception
2014 ILSVRC winner
在Inception网络中,一个卷积层包含多个不同大小的卷积操作,称为Inception模块,并将得到的特征映射在深度上拼接起来作为输出特征映射。
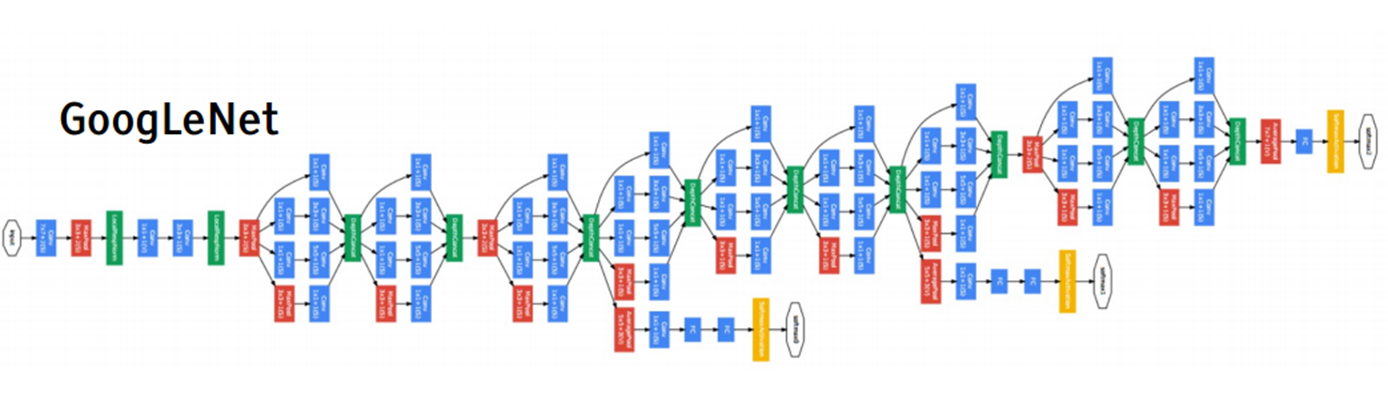
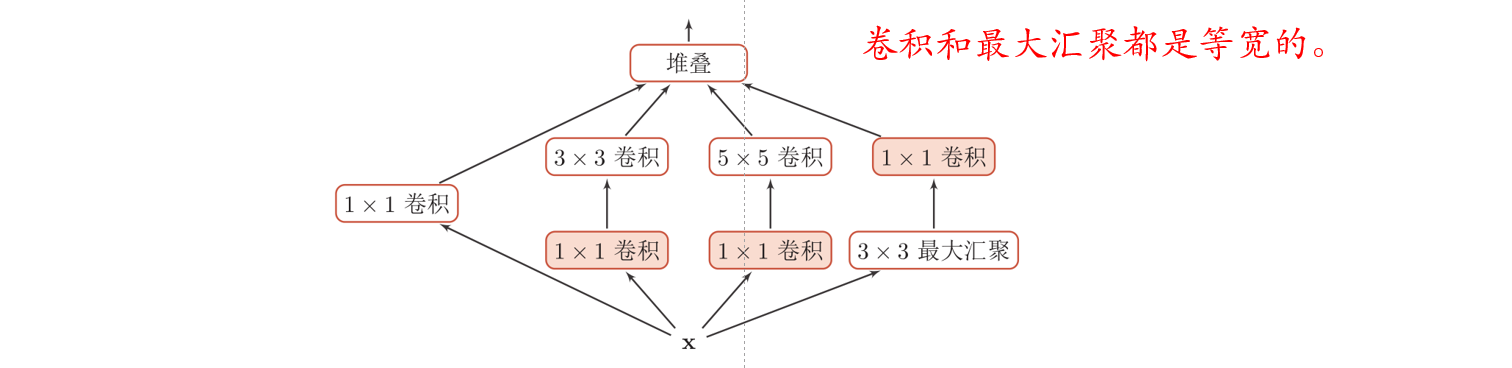
在Inception v3中,用了多层小卷积核代替了大卷积核,进一步降低了计算量和参数量
ResNet
残差网络:是通过给非线性的卷积层增加直连边的方式来提高信息的传播效率。假设在一个深度网络中,我们期望一个非线性单元$f(x;\theta)$去逼近一个目标函数为$h(x)$,可以将目标函数拆成恒等函数(不可逼近)和残差函数(可逼近)两个部分。
$$
h(\pmb x) = \pmb x+ (h(\pmb x)-\pmb x) \approx \pmb x+f(\pmb x;\theta)
$$
其中,直连边可以直接传递恒等函数,即$\pmb x$的部分,由中间的卷积部分去逼近残差函数的部分。
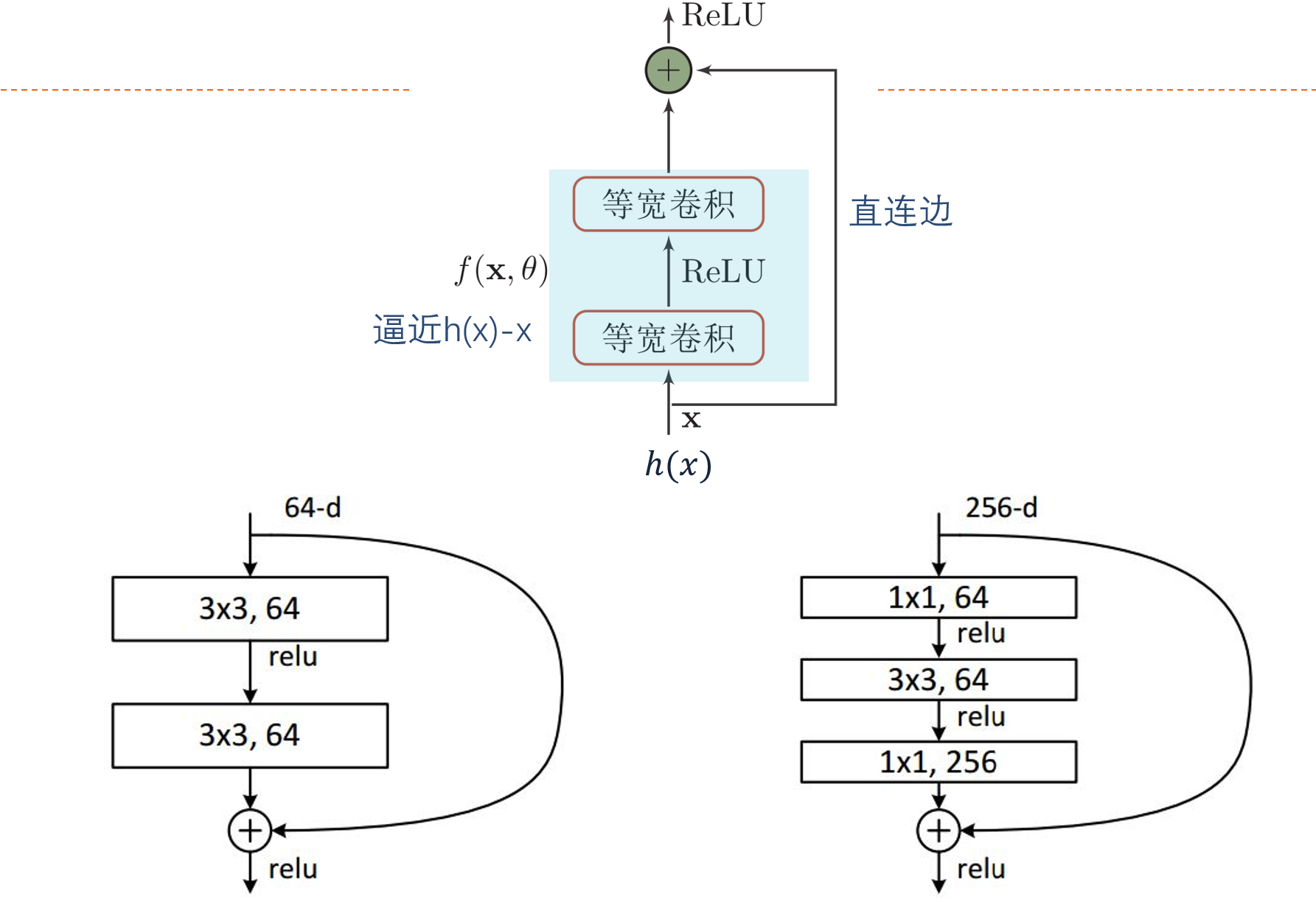
对于含残差的函数,可以得到
$$
h ^\prime(x) = 1+{\partial f(\pmb x;\theta) \over \partial \pmb x}
$$
导数中有一个常数1,因此导数值无论如何不会过低,也降低了出现梯度消失的可能性。
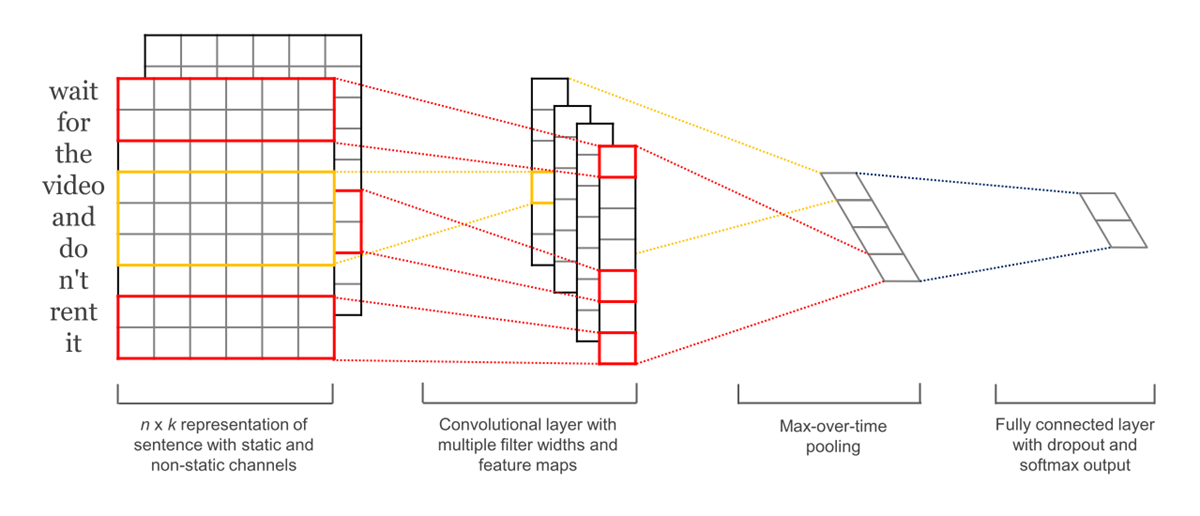
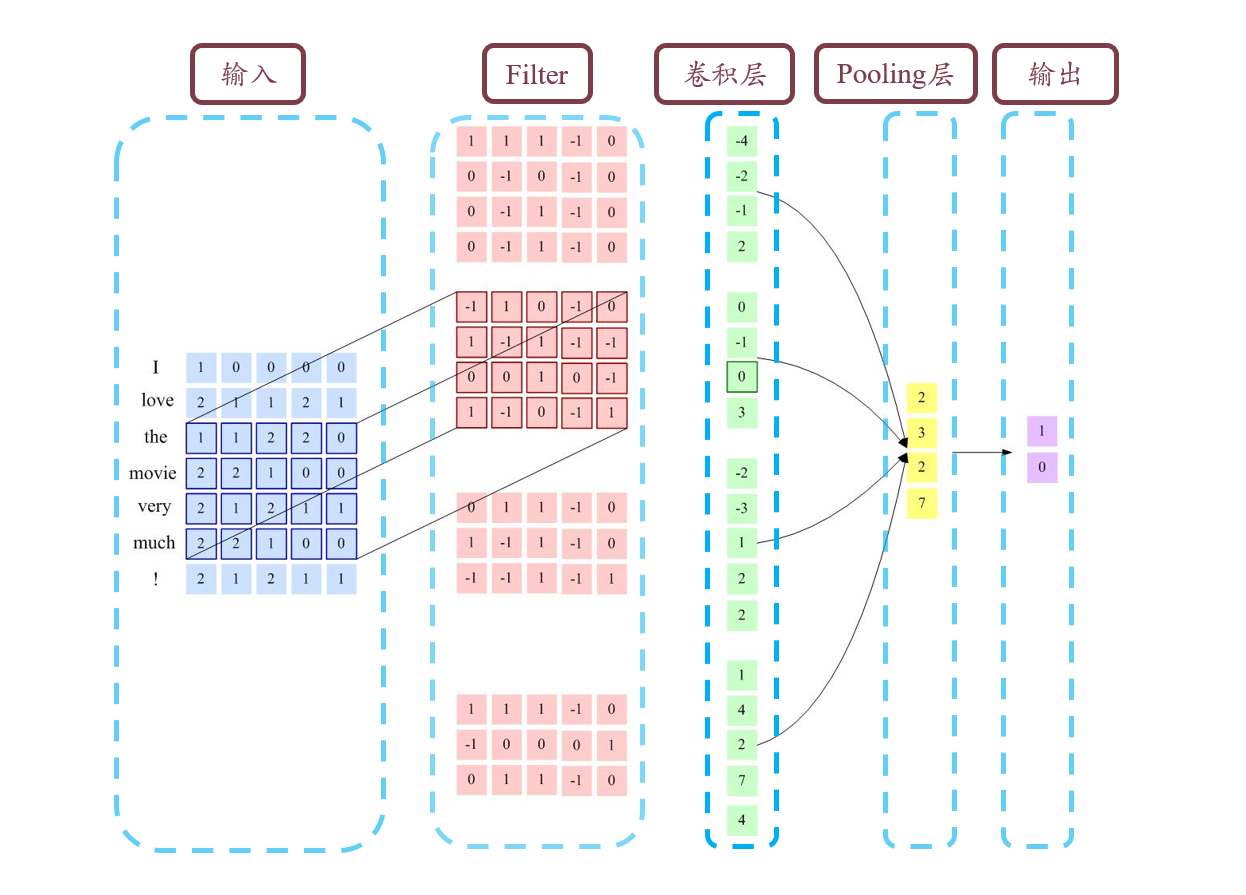
文本序列卷积
以部分的单词编码为基础,卷积核不一定保持size一致,需要在池化层通过采用时间维度pooling等手段将句子卷积结果合并到一起,形成合理的维度结构。