本文最后更新于:几秒前
动态规划
数字三角形模型
与摘花生不同,本题要求的是路径走两次,且在走的过程中,若之前方格的数字中有被使用,则第二次不可使用。因此这道题的两个路径之间本身就有一定的关联性。
从摘花生的集合状态与属性出发,f(i,j)代表从开头(1,1)到(i,j)的最佳路径,因为此题走了两次,因此可以稍加推广,以f(i1,j1,i2,j2)表示第一次走到(i1,j1),第二次走到(i2,j2)的数值最大值,这里的思路和平时不一样,同时处理两条路径的走向。
又根据题目要求,两个路径存在的主要矛盾是当路径重合使用时的数值使用问题,又因若使两个路径可能有重合,则两个路径的步数一定是一致的,因此设置一个同步变量k = i1+j1 = i2+j2,将集合状态换成f(k,i1,i2),j1和j2均可通过此状态推导出来。这里可以形象的理解为状态从左上角到右下角成弧形扩散
∴以f(k,i1,i2)表示所有从(1,1)分别走到(i1,j1)和(i2,j2)的最大值。
转移时,因为上一个状态转到下一个状态的动作是”行走”动作,故可以将状态转移抽象成两个路径分别向(下,下)、(下,右)、(右,下)、(右,右)的转移。即
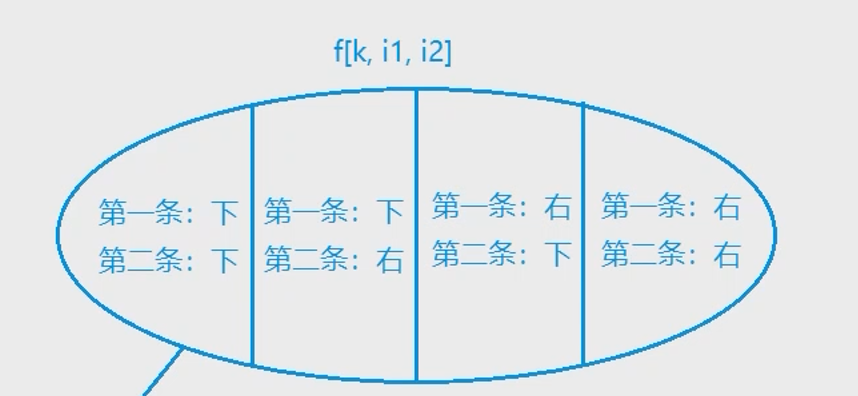
对每一种情况的状态转移,首先需要判断是否走到一起。
1
2
3
|
if(i1==i2) t = w[i1][j1];
else t = w[i1][j1]+w[i2][j2];
|
以两个路径都向下为例:
1
| f[k][i1][j1]=max(f[k][i1][i2],f[k-1][i1-1][i2-1]+t);
|
代码如下,注意注释内容
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N= 25;
int n,w[N][N],f[N*2][N][N];
int main(){
cin >> n;int r,c,p;
while(cin>>r>>c>>p && r||c||p){
w[r][c] = p;
}
for(int k = 2;k <= n*2;k++){
for(int i1 = 1;i1 <= n;i1++){
for(int i2 = 1;i2 <= n;i2++){
int j1 = k-i1,j2 = k-i2;
int t = w[i1][j1];
if(i1!=i2) t+=w[i2][j2];
int &x=f[k][i1][i2];
x = max(x,f[k-1][i1-1][i2-1]+t);
x = max(x,f[k-1][i1-1][i2]+t);
x = max(x,f[k-1][i1][i2-1]+t);
x = max(x,f[k-1][i1][i2]+t);
}
}
}
cout << f[2*n][n][n];
return 0;
}
|
和方格取数一模一样,证明如下:
最长上升子序列模型(LIS)
此题可以抽象为正序、倒序各做一次最长上升子序列问题(LIS),这里主要给出两种可行的最长上升子序列求解办法。
DP(O(n2))
用一个数组F[i]代表以A[i]结尾的LIS的长度,状态转移时两层循环,最外层i循环每个数,内层循环j循环i前面的每个数,F[i] = max{F[j]+1,F[i]}
代码如下:
1
2
3
4
5
6
7
8
| for(int i = 1;i <= m;i++){
g[i]=1;
for(int j = 1;j < i;j++){
if(f[j]<f[i]) g[i]=max(g[i],g[j]+1);
}
res = max(res,g[i]);
}
|
二分+贪心(O(nlogn))
原理:
题解中最难理解的地方在于栈中序列虽然递增,但是每个元素在原串中对应的位置其实可能是乱的,那为什么这个栈还能用于计算最长子序列长度?
实际上这个栈【不用于记录最终的最长子序列】,而是【以stk[i]结尾的子串长度最长为i】或者说【长度为i的递增子串中,末尾元素最小的是stk[i]】。理解了这个问题以后就知道为什么新进来的元素要不就在末尾增加,要不就替代第一个大于等于它元素的位置。
这里的【替换】就蕴含了一个贪心的思想,对于同样长度的子串,我当然希望它的末端越小越好,这样以后我也有更多机会拓展。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| #include<iostream>
using namespace std;
const int N = 100010;
int f[N],n;
int g[N];
int main(){
cin >> n;
for(int i = 1;i <= n;i++)cin >> f[i];
g[1] = f[1];
int t = 1;
for(int i = 2;i <= n;i++){
if(g[t] < f[i]){
g[t+1] = f[i];
t++;
}
else {
int l = 1,r = t;
while(l < r){
int m = (l+r)/2;
if(g[m] >= f[i]) r = m;
else l = m+1;
}
g[l] = f[i];
}
}
cout << t << endl;
return 0;
}
|
此题是LIS问题的一个变型,需要求的是以中间为最大值,两端降低的子序列,我们直接从前到后和从后到前,一共两次求解最长上升和最长下降子序列,然后迭代每个位置求和即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n,f[N],g[N],k[N];
int main(){
cin >> n;
for(int i = 0;i < n;i++)cin >> f[i];
for(int i = 0;i < n;i++){
g[i]=1;
for(int j = 0;j < i;j++){
if(f[j]<f[i]) g[i]=max(g[i],g[j]+1);
}
}
for(int i = n-1;i >= 0;i--){
k[i]=1;
for(int j = n-1;j>i;j--){
if(f[j]<f[i]) k[i]=max(k[i],k[j]+1);
}
}
int res=0;
for(int i = 0;i < n;i++){
res=max(res,g[i]+k[i]-1);
}
cout << res;
return 0;
}
|
此题可以理解为对Pair求解LIS问题,首先对first部分进行排序,使其有一定的次序,然后对Pair的每一维都进行LIS问题的求解。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| #include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int N = 5010;
typedef pair<int,int> PII;
vector<PII> v;
int res,g[N];
bool cmp(const PII a,const PII b){
return a.first<b.first;
}
int main(){
int n;cin >> n;
for(int i = 0;i < n;i++){
int l,r;cin >> l >> r;
v.push_back({l,r});
}
sort(v.begin(),v.end(),cmp);
for(int i = 0;i < n;i++){
g[i]=1;
for(int j = 0;j < i;j++){
if(v[j].first < v[i].first && v[j].second < v[i].second) g[i]=max(g[i],g[j]+1);
}
res=max(res,g[i]);
}
cout << res << endl;
return 0;
}
|
令LIS问题DP解法中的g[i]表示以f[i]为结尾的最长上升子序列和,这样LIS的转移方法仍然适用于这道题。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int f[N],g[N],res;
int main(){
int n;
cin >> n;
for(int i =0;i < n;i++)cin >> f[i];
for(int i =0;i < n;i++){
g[i]=f[i];
for(int j = 0;j < i;j++){
if(f[j]<f[i]) g[i]=max(g[i],g[j]+f[i]);
}
res=max(res,g[i]);
}
cout << res;
return 0;
}
|
这里我们按照以下几个部分来讲:
问题的第一部分是最长下降子序列,直接代板子,不再赘述
问题的第二部分是找到最少个数的下降子序列将序列覆盖
第二问可以采用贪心的做法,这里可以复习最长上升子序列的贪心解法。考虑一种贪心方案:
对于第i个数来说,把它加入前 i - 1 个数构成的下降子序列组中,所有结尾元素大于第i个数的数中最小的那个数,下给出对其的证明:
假设有一种最优策略不是按照贪心策略进行求解的,则可以通过有限步的调整将最优解调整成贪心解,且不改变原有条件要求。
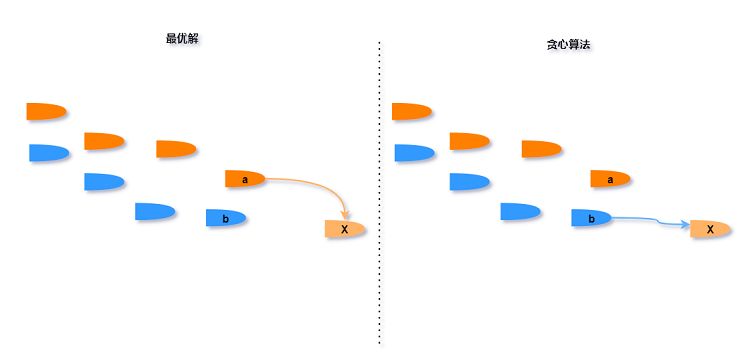
因此可以每次找到序列尾部一个大于等于当前值的最小值并加入,如果所有的序列最后一个都小于当前值,则另开一个新的序列,这保证了记录序列尾部的数组一定是单调递增的,因为每次加入的都是大于所有值的新数。
1
2
3
4
5
6
7
8
9
10
11
12
|
int cnt=0;
for(int i = 0;i < n;i++){
int t=0;
while(t <cnt && g[t]<f[i]) t++;
g[t]=f[i];
if(t>=cnt) cnt++;
}
|
注:此道题由于满足Dilworth定理:偏序集的最少反链划分数等于最长链的长度,因此求最少的下降子序列划分数,等同于求上升子序列的最长长度,因此这里可以直接求一个最长上升子序列并给出解。
这是两个经典DP问题$(LIS和LCS)$的结合版,按照集合的概念理解DP
状态表示$f[i][j]$—集合:考虑 a 中前 i 个数字,b 中前 j 个数字 ,且当前以 b[j] 结尾的子序列的方案
状态表示$f[i][j]$—属性:该方案的子序列长度最大$max$
状态转移 :
a数组中前 i-1个数字,b数组中前 j 个数字 ,且当前以 b[j] 结尾的子序列的方案转移过来:$f_{i,j}=max(f_{i,j},f_{i−1,j})$,此时$a[i]\ne b[j]$
a数组中前 i 个数字,b数组中前 k 个数字 ,且当前以 b[k] 结尾的子序列的方案转移过来:$f_{i,j}=max(f_{i,j},f_{i−1,k+1}),k∈[0,j−1],a[i]==b[j],bj>bk$
其中,对于第二种情况需要从j-1种可能的情况转移过来,难度较大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| #include<iostream>
#include<algorithm>
#include<vector>
#include<cstring>
using namespace std;
const int N = 3010;
int n,d[N][N];
int a[N],b[N];
vector<int> s;
int main(){
cin >> n;
for(int i = 1;i <= n;i++)cin >> a[i];
for(int i = 1;i <= n;i++)cin >> b[i];
for(int i = 1;i <= n;i++){
int maxv=1;
for(int j = 1;j <= n;j++){
d[i][j] = d[i-1][j];
if(a[i]==b[j]) d[i][j] = max(d[i][j],maxv);
if(b[j]<a[i]) maxv=max(maxv,d[i-1][j]+1);
}
}
int res=0;
for(int i = 1; i<=n;i++) res = max(res,d[n][i]);
cout << res;
return 0;
}
|

