模型独立的学习方式笔记

模型独立的学习方式

不同的学习方式

这些学习方式不限于具体的模型，但一种学习方式会对具有某种特质的模型更加青睐。

集成学习

集成学习的目的在于通过某种策略将多个模型集成起来，通过群体决策来提高决策准确率。

直接平均（投票）

定理10-1：对于$M$个不同的模型$f_1(\pmb x),…,f_M(\pmb x)$，其平均期望错误为$\overline {\mathcal R}(f)$，基于简单投票机制的集成模型$f^{(c)}(\pmb x)={1 \over M}\sum_{m=1}^Mf_m(\pmb x)$的期望错误理论在${1\over M}\overline {\mathcal R}(f)$和$\overline {R}(f)$之间。

证明：
$$
\begin{align}
\mathcal R(f) & = \mathbb E_x[({1\over M}\sum_{m=1}^ Mf_m(\pmb x)-h(\pmb x))^2] \\
& = \mathbb E_x[{1\over M^2}\sum_{m=1}^ M(f_m(\pmb x)-h(\pmb x))^2] \\
& = {1\over M^2}\mathbb E_x[\sum_{m=1}^ M\epsilon_m(\pmb x)^2]\\
& = {1\over M^2}\sum_{m=1}^ M\sum_{n=1}^ N\mathbb E_x[\epsilon_m(\pmb x)\epsilon_n(\pmb x)]\\
\end{align}
$$
其中$\mathbb E_x[\epsilon_m(\pmb x)\epsilon_n(\pmb x)]$是模型错误的相关性，若模型不相关，则有$\forall m\ne n，\mathbb E_x[\epsilon_m(\pmb x)\epsilon_n(\pmb x)]=0$；若模型完全相同相关，则有$\forall m\ne n,\epsilon_m(\pmb x)=\epsilon_n(\pmb x)$，那么则有：$\overline {\mathcal R}(f)\ge \mathcal R(f)\ge{1\over M}\overline {\mathcal R}(f)$

证毕。

根据证明过程可知，基分类器应当差异越大越好。

Bagging类

通过不同模型的训练数据集的独立性来提高不同模型之间的独立性。实现方式是在原数据集上进行有放回的随机采样，得到$M$个比较小的训练集并训练$M$个模型，然后通过简单投票进行集成。

随机森林

在Bagging基础上引入随机特征，进一步提高每个基模型间的独立性。

Boosting类

按照一定的顺序先后训练不同的模型，前序模型指导后续模型的训练，每次训练时根据前序模型的结果调整权重。

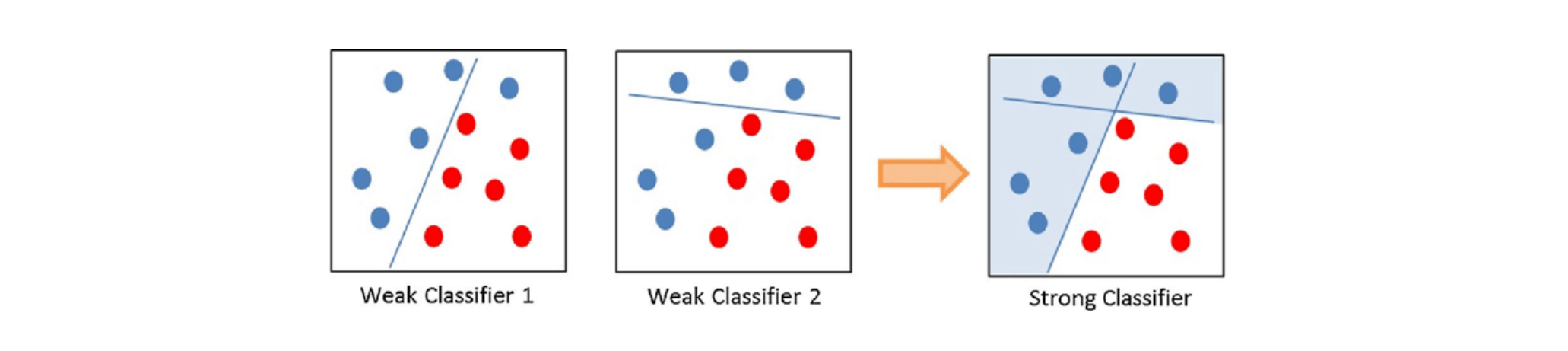
Adaboost

Boosting类集成模型目标是学习一个加性模型：
$$
F(\pmb x)=\sum_{m=1}^M \alpha_mf_m(\pmb x)
$$
其中$f_m(\pmb x)$是基分类器，$\alpha_m$是权重，Adaboost算法的过程是这样的：假设已经训练了第$m$个基分类器，在训练第$m+1$个基分类器的时候提高分错样本的权重，使得第$m+1$个基分类器更关注分错的样本。以二分类为例：

其中，加权错误率$\epsilon_m$的计算在此不再叙述，自行查阅相关文献；权重更新时是通过损失最小来进行更新。

自训练和协同训练

自训练和协同训练一般用在半监督学习中，使用少量标注数据和大量无标注数据来训练模型。

自训练

自训练是首先使用标注数据来训练一个模型，并使用这个模型来预测无标注样本的标签，把预测置信度比较高的样本及其预测的伪标签加入训练集，然后重新训练新的模型，并不断重复这个过程。

协同训练

协同训练是在自训练基础上的改进，通过两个基于不同视角的分类器来互相促进。比如互联网上的每个网页都由两种视角组成：文字内容（text）和指向其他网页的链接，如果要确定一个网页的类别，既可以根据文字内容来判断，也可根据网页之间的链接关系来判断。

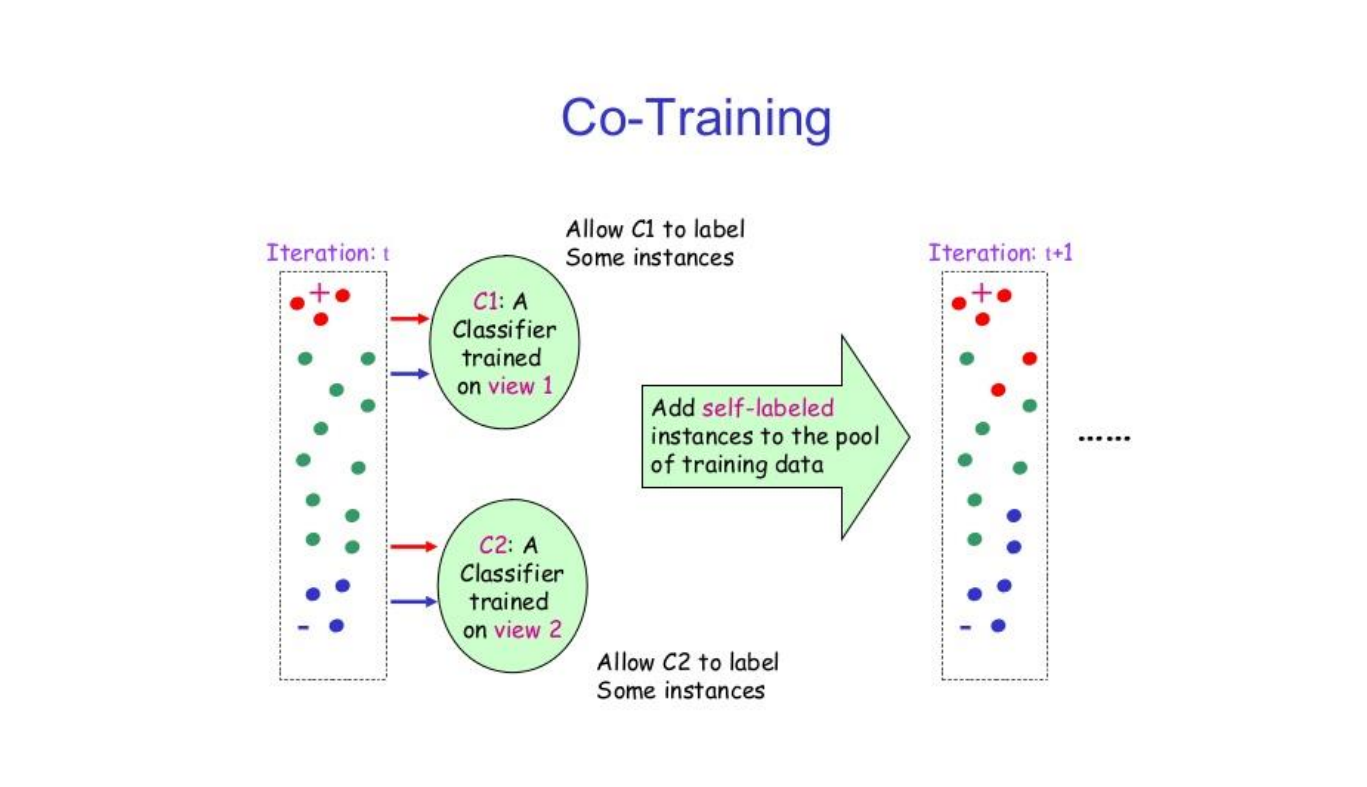
与自训练不同的是，协同训练是两个互补模型一起标注无标签数据并加入。

由于不同视角的条件独立性，在不同视角上训练出来的模型就相当于从不同视角来理解问题，具有一定的互补性．协同训练就是利用这种互补性来进行自训练的一种方法。

多任务学习

多任务学习（Multi-task Learning）是指同时学习多个相关任务，让这些任务在学习过程中共享知识，利用多个任务之间的相关性来改进模型在每个任务上的性能和泛化能力．多任务学习可以看作一种归纳迁移学习（Inductive Transfer Learning），即通过利用包含在相关任务中的信息作为归纳偏置（Inductive Bias）来提高泛化能力。

（归纳偏置：关于目标函数的必要假设）

多任务学习有以下几种的学习模式：

• 硬共享模式：底层共享，高层特用；
• 软共享模式：任务间共享信息，如隐状态、注意力等；
• 层次共享模式：底层提取低级局部特征，高层提取抽象语义特征；
• 共享-私有模式：共享模块与特定（私有）模块分开提取特征；

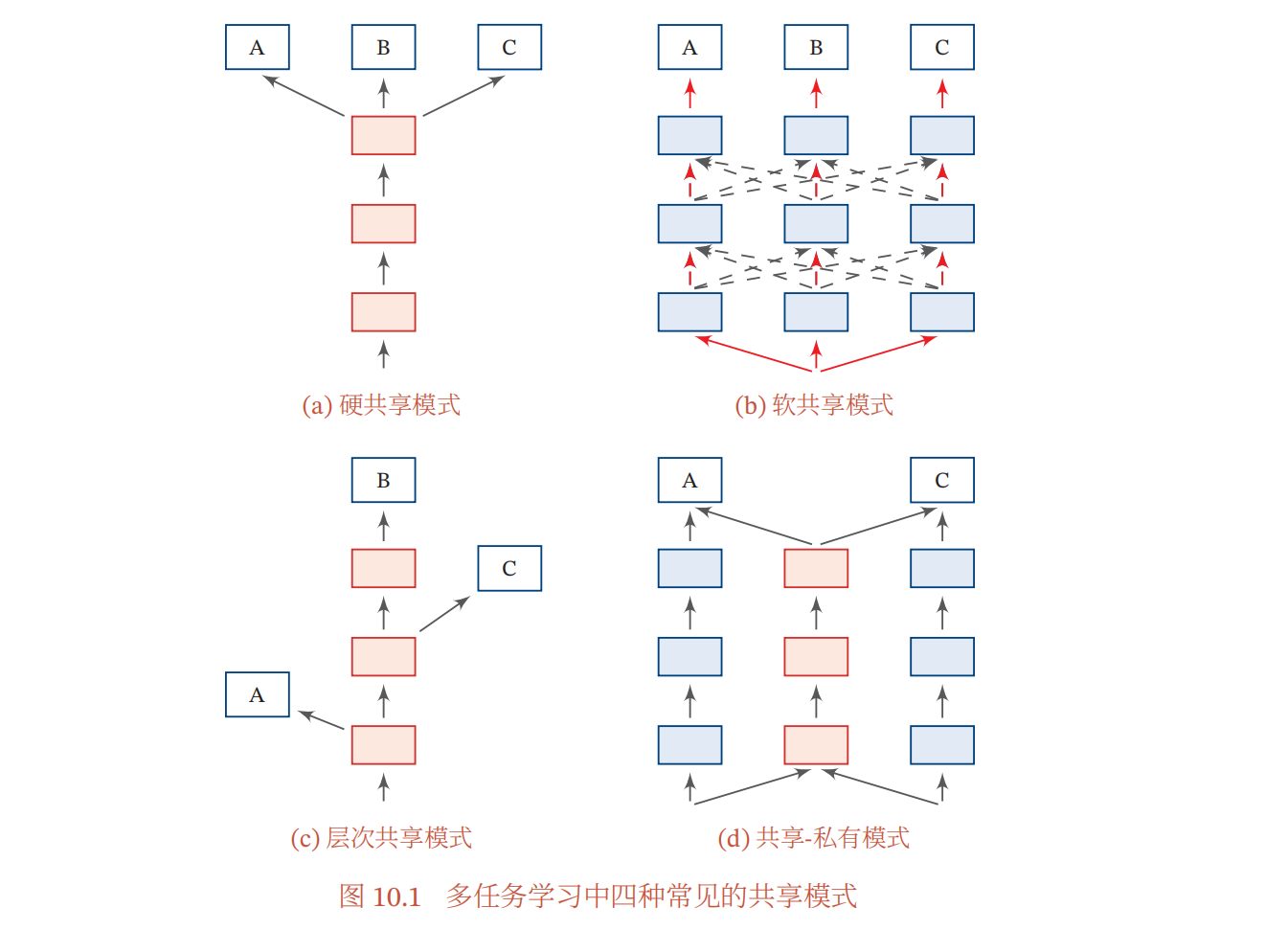
损失函数

多任务学习的损失函数是所有任务的损失函数的线性加权：
$$
\mathcal L(\theta)=\sum_{m=1}^M\sum_{n=1}^N\eta_m\mathcal L_m(f_m(x^{(m,n)};\theta),y^{(m,n)})
$$
其学习流程分为联合训练和单任务精调两个阶段，分别对应于泛化任务和特化任务。

迁移学习

迁移学习的目标在于从已有的大规模的与目标任务分布不同的训练数据中学习到普遍使用的可泛化知识，将其迁移到目标任务上。

假设一个机器学习任务$\mathcal T$的样本空间为$\mathcal X\times \mathcal Y$，其中$\mathcal X$是输入空间，$\mathcal Y$是输出空间，概率密度函数为$p(\pmb x,y)$，一个样本空间及其分布可以称作一个领域$\mathcal D=(\mathcal X,\mathcal Y,p(\pmb x,y))$；一个机器学习任务的定义是在一个领域$\mathcal D$上的条件概率$p(\pmb x|y)$的建模问题。

迁移学习的本质是不同领域的知识迁移过程，利用源领域$\mathcal D_S$中学到的知识来帮助目标领域$\mathcal D_T$上的学习任务，源领域的训练样本数量一般远大于目标领域。

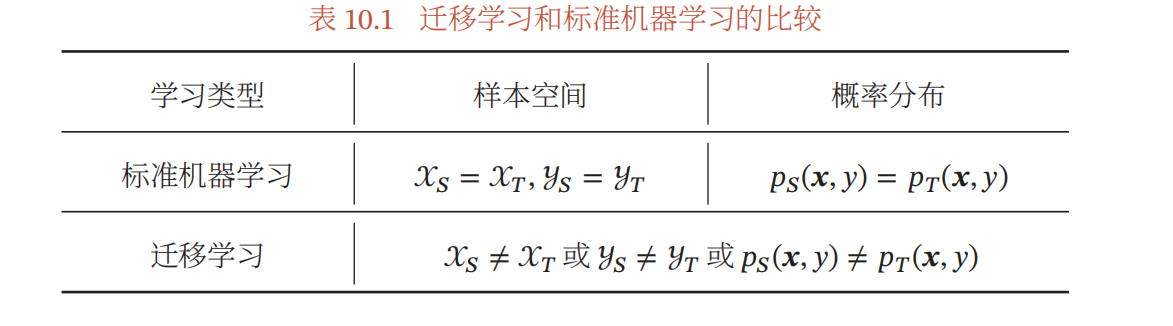
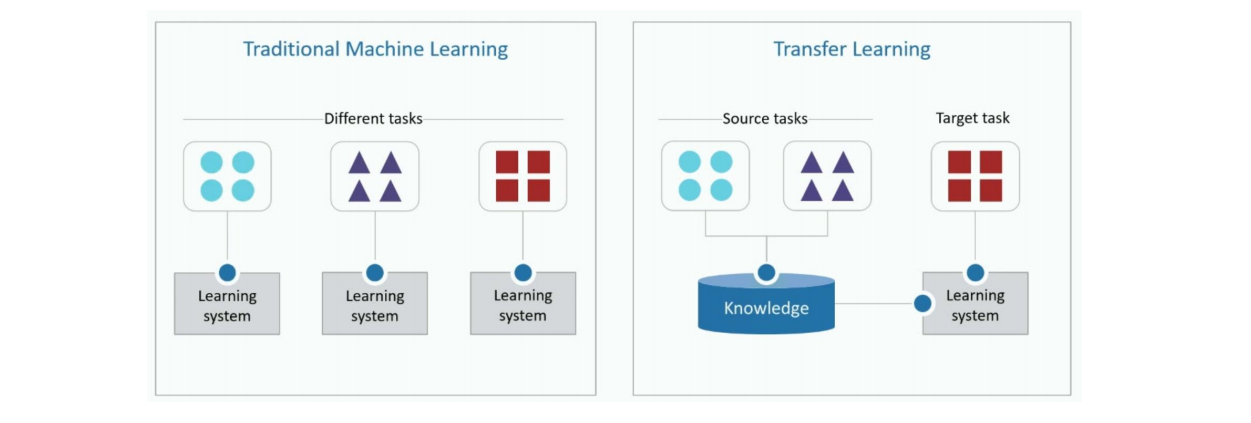
迁移学习根据不同的迁移方式分成两种类型：

• 归纳迁移学习：对应于归纳学习，指在源领域和任务上学习出一般的规律，然后将这个规律迁移到目标领域和任务上。（基于特征或精调）
  • 与多任务学习的不同：有先后次序，先源领域学习，后目标领域迁移。
• 转导迁移学习：是一种从样本到样本的迁移，直接利用源领域和目标领域的样本进行迁移学习。
  • 转导迁移学习的一个常见子问题是领域适应，一般假设源领域和目标领域有相同的样本空间，但是数据分布不同，即$p_s(\pmb x,y)\ne p_t(\pmb x,y)$。
  • 三种情况导致分布不同：协变量偏移（$p(\pmb x)$）/概念偏移（$p(y|\pmb x)$）/先验偏移（$p(y)$）
  • 协变量偏移：一般指输入在训练集和测试集上的分布不同．这样，在训练集上学习到的模型在测试集上的表现会比较差。

元学习

元学习指的是能够通过动态调整模型超参或动态选择模型来适应不同任务的特点，又可称为“学习的学习”，和元学习比较相关的一个机器学习问题是小样本学习，即在小样本上的快速学习能力。

• 基于优化器的元学习

  • 用一个模型预测梯度下降时的梯度差值$\triangle \delta_t=\delta_t-\delta_{t-1}$，其优化器为$g_t(·)$，则第$t$步的更新规则就可以写成$\delta_t+1=\delta_t+g_t(\nabla\mathcal L(\delta_t);\phi)$。其目标函数为：
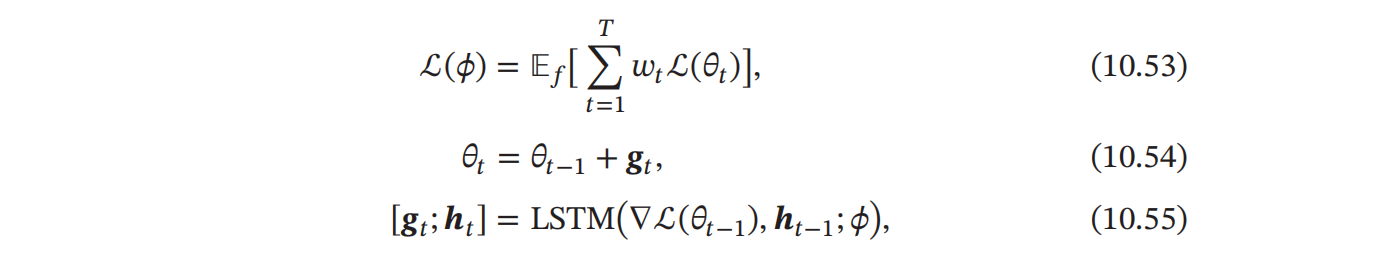  • ，其中$LSTM$网络可以看作一个更为高阶的学习模型，学习的是原模型的学习方式。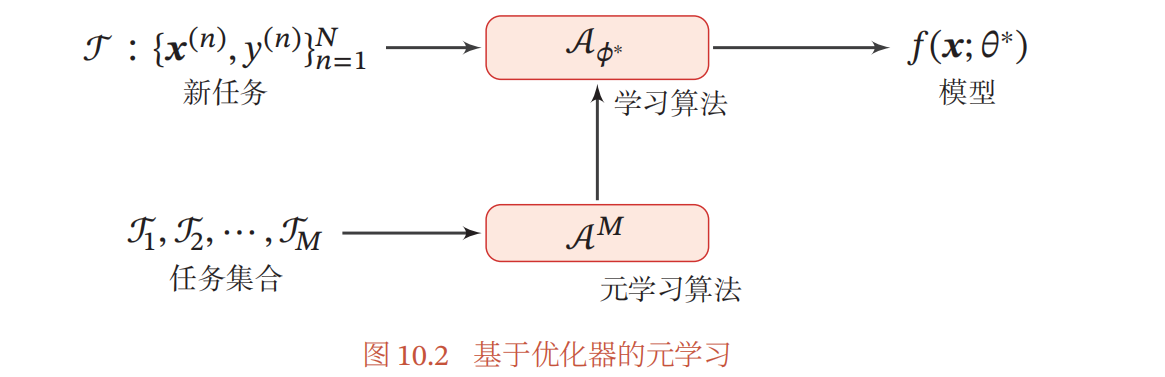
  • 

• 模型无关的元学习

  • 是一个简单的模型无关、任务无关的元学习算法，表示为在任务空间中的所有任务上学习一种通用的表示。MAML方法提倡采用一种折中的方式，即通过将多个任务的损失函数进行平均，而后用平均损失函数对模型参数求导，得到参数的梯度方向。

  • $$
    =\min_{\theta}\sum_{\mathcal F_m~p(\mathcal F)}\mathcal L_{\mathcal F_m}(f(\underbrace{\theta-\alpha\nabla_\theta\mathcal L_{\mathcal F_m}(f_\theta))}_{\theta’_m})
    $$

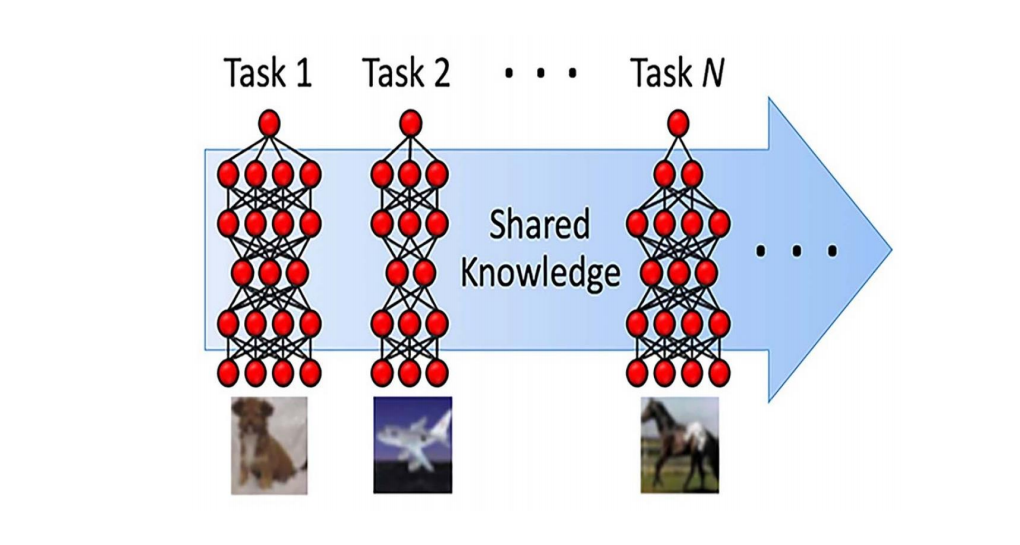
终身学习

人类的学习是一直持续的，人脑可以通过记忆不断地累积学习到的知识，这些知识累积可以在不同的任务中持续进行。和归纳迁移学习一样，终身学习也是在前$m$个任务中学习，不过终身学习关注于对前$m$个任务的知识的积累过程。

在终身学习中，一个关键的问题是如何避免“灾难性遗忘”，即按照一定顺序学习多个任务时，在学习新任务的同时不忘记先前学会的历史任务。

弹性权重巩固

以两个任务的持续学习为例，假设任务$\mathcal T_A$和任务$\mathcal T_B$的数据集分别为$\mathcal D_A$和$\mathcal D_B$，从贝叶斯角度看，将模型参数$\theta$看作随机变量，给定两个任务时$\theta$的后验分布为：
$$
\log p(\theta|\mathcal D) = \log p(\mathcal D|\theta)+\log p(\theta)-\log p(\mathcal D), 其中\mathcal D = \mathcal D_A \cup \mathcal D_B
$$
根据独立同分布假设，上式可以写为：
$$
\begin{align}
\log p(\theta|\mathcal D) & = \underline{\log p(\mathcal D_A|\theta)}+\log p(\mathcal D_B|\theta)+\underline{\log p(\theta)}-\underline{\log p(\mathcal D_A)}-\log p(\mathcal D_B) \\
& = \log p(\mathcal D_B|\theta)+\underline{\log p(\theta|\mathcal D_A)}-\log p(\mathcal D_B)
\end{align}
$$
其中$\log p(\theta|\mathcal D_A)$包含所有在任务$\mathcal T_A$上学到的信息，当顺序的学习任务$\mathcal T_B$时，参数在两个任务上的后验分布和其在任务$\mathcal T_A$的后验分布有关。

由于后验分布难以建模，因此可以用精度矩阵（协方差矩阵的逆）来近似：
$$
p(\theta|\mathcal D_A)=\mathcal N(\theta_A^*,F^{-1})
$$
其中$F$是$Fisher$信息矩阵，为了提高计算效率，$F$可以简化为对角阵。