神经网络与深度学习实验二——机器学习基础

本文最后更新于：几秒前

此实验对应NNDL书第二章

机器学习的要素

数据

在实践中，数据的质量会很大程度上影响模型最终的性能，通常数据预处理是完成机器学习实践的第一步，噪音越少、规模越大、覆盖范围越广的数据集往往能够训练出性能更好的模型。数据预处理可分为两个环节：先对收集到的数据进行基本的预处理，如基本的统计、特征归一化和异常值处理等；再将数据划分为训练集、验证集（开发集）和测试集。

  • 训练集：用于模型训练时调整模型的参数，在这份数据集上的误差被称为训练误差；
  • 验证集（开发集）：对于复杂的模型，常常有一些超参数需要调节，因此需要尝试多种超参数的组合来分别训练多个模型，然后对比它们在验证集上的表现，选择一组相对最好的超参数，最后才使用这组参数下训练的模型在测试集上评估测试误差。
  • 测试集：模型在这份数据集上的误差被称为测试误差。训练模型的目的是为了通过从训练数据中找到规律来预测未知数据，因此测试误差是更能反映出模型表现的指标。

数据划分时要考虑到两个因素：更多的训练数据会降低参数估计的方差，从而得到更可信的模型；而更多的测试数据会降低测试误差的方差，从而得到更可信的测试误差。如果给定的数据集没有做任何划分，我们一般可以大致按照7:3或者8:2的比例划分训练集和测试集，再根据7:3或者8:2的比例从训练集中再次划分出训练集和验证集。

需要强调的是，测试集只能用来评测模型最终的性能，在整个模型训练过程中不能有测试集的参与。

模型

我们希望能让计算机从一个函数集合 $\mathcal{F} = {f_1(\boldsymbol{x}), f_2(\boldsymbol{x}), \cdots }$中自动寻找一个“最优”的函数$f^∗(\boldsymbol{x})$ 来近似每个样本的特征向量 $\boldsymbol{x}$ 和标签 $y$ 之间
的真实映射关系，实际上这个函数集合也被称为假设空间，在实际问题中，假设空间$\mathcal{F}$通常为一个参数化的函数族
$$
\mathcal{F}=\lbrace f(\boldsymbol{x};\theta)\mid\theta\in\mathbb{R}^{D} \rbrace, (2.1)
$$
其中$f(\boldsymbol{x} ; \theta)$是参数为$\theta$的函数，也称为模型，𝐷为参数的数量。

常见的假设空间可以分为线性和非线性两种，对应的模型 $f$ 也分别称为线性模型和非线性模型。线性模型的假设空间为一个参数化的线性函数族，即：
$$
f(\boldsymbol{x} ; \theta)=\boldsymbol{w}^{\top} \boldsymbol{x}+b, (2.2)
$$
其中参数$\theta$ 包含了权重向量$\boldsymbol{w}$和偏置$b$。

线性模型可以由非线性基函数$\phi(\boldsymbol{x})$变为非线性模型，从而增强模型能力:

$$
f(\boldsymbol{x} ; \theta)=\boldsymbol{w}^{\top} \phi(\boldsymbol{x})+b, (2.3)
$$
其中$\phi(\boldsymbol{x})=\left[\phi_{1}(\boldsymbol{x}), \phi_{2}(\boldsymbol{x}), \cdots, \phi_{K}(\boldsymbol{x})\right]^{\top}$为𝐾 个非线性基函数组成的向量，参数 $\theta$ 包含了权重向量$\boldsymbol{w}$和偏置$b$。

学习准则

为了衡量一个模型的好坏，我们需要定义一个损失函数$\mathcal{L}(\boldsymbol{y},f(\boldsymbol{x};\theta))$。损失函数是一个非负实数函数，用来量化模型预测标签和真实标签之间的差异。常见的损失函数有 0-1 损失、平方损失函数、交叉熵损失函数等。

机器学习的目标就是找到最优的模型$𝑓(𝒙;\theta^∗)$在真实数据分布上损失函数的期望最小。然而在实际中，我们无法获得真实数据分布，通常会用在训练集上的平均损失替代。

一个模型在训练集$\mathcal{D}={(\boldsymbol{x}^{(n)},y^{(n)})}_{n=1}^N$上的平均损失称为经验风险{Empirical Risk}，即:

$$
\mathcal{R}^{emp}_ \mathcal{D}(\theta)=\frac{1}{N}\sum_{n=1}^{N}\mathcal{L}(y^{(n)},f({x}^{(n)};\theta))。 (2.4)
$$
$\mathcal{L}(\boldsymbol{y},f(\boldsymbol{x};\theta))$为损失函数。损失函数是一个非负实数函数，用来量化模型预测和真实标签之间的差异。常见的损失函数有0-1损失、平方损失函数、交叉熵损失函数等。

在通常情况下，我们可以通过使得经验风险最小化来获得具有预测能力的模型。然而，当模型比较复杂或训练数据量比较少时，经验风险最小化获得的模型在测试集上的效果比较差。而模型在测试集上的性能才是我们真正关心的指标．当一个模型在训练集错误率很低，而在测试集上错误率较高时，通常意味着发生了过拟合（Overfitting）现象。为了缓解模型的过拟合问题，我们通常会在经验损失上加上一定的正则化项来限制模型能力。

过拟合通常是由于模型复杂度比较高引起的。在实践中，最常用的正则化方式有对模型的参数进行约束，比如$\ell_1$或者$\ell_2$范数约束。这样，我们就得到了结构风险（Structure Risk）。
$$
\mathcal{R}^{struct}_ {\mathcal{D}}(\theta)=\mathcal{R}^{emp}_{\mathcal{D}}(\theta)+\lambda \ell_p(\theta), (2.5)
$$

其中$\lambda$为正则化系数，$p=1$或$2$表示$\ell_1$或者$\ell_2$范数。

优化算法

在有了优化目标之后，机器学习问题就转化为优化问题，我们可以利用已知的优化算法来学习最优的参数。当优化函数为凸函数时，我们可以令参数的偏导数等于0来计算最优参数的解析解。当优化函数为非凸函数时，我们可以用一阶的优化算法来进行优化。

目前机器学习中最常用的优化算法是梯度下降法(Gradient Descent Method)。当使用梯度下降法进行参数优化时，还可以利用验证集来早停法(Early-Stop)来中止模型的优化过程，避免模型在训练集上过拟合。早停法也是一种常用并且十分有效的正则化方法。

评估指标

评估指标(Metric)用于评价模型效果，即给定一个测试集，用模型对测试集中的每个样本进行预测，并根据预测结果计算评价分数。回归任务的评估指标一般有预测值与真实值的均方差，分类任务的评估指标一般有准确率、召回率、F1值等。

对于一个机器学习任务，一般会先确定任务类型，再确定任务的评价指标，再根据评价指标来建立模型，选择学习准则。由于评价指标不可微等问题有时候学习准则并不能完全和评价指标一致，我们往往会选择一定的损失函数使得两者尽可能一致。

实现线性回归

回归函数

1
2
3
4
# 真实函数的参数缺省值为 w=1.2，b=0.5
def linear_func(x,w=1.2,b=0.5):
    y = w*x + b
    return y

数据生成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import paddle

def create_toy_data(func, interval, sample_num, noise = 0.0, add_outlier = False, outlier_ratio = 0.001):
    """
    根据给定的函数，生成样本
    输入：
       - func：函数
       - interval： x的取值范围
       - sample_num： 样本数目
       - noise： 噪声均方差
       - add_outlier：是否生成异常值
       - outlier_ratio：异常值占比
    输出：
       - X: 特征数据，shape=[n_samples,1]
       - y: 标签数据，shape=[n_samples,1]
    """

    # 均匀采样
    # 使用paddle.rand在生成sample_num个随机数,随机数用什么都可以
    # 乘法放大到interval范围，interval[0]移动到以范围中点为中心
    X = paddle.rand(shape = [sample_num]) * (interval[1]-interval[0]) + interval[0]
    
    y = func(X)

    # 生成高斯分布的标签噪声
    # 使用paddle.normal生成0均值，noise标准差的数据,大小为y的输出张量
    # 同理于torch.normal方法
    epsilon = paddle.normal(0,noise,paddle.to_tensor(y.shape[0]))
    y = y + epsilon
    # 生成额外的异常点
    if add_outlier:     
        outlier_num = int(len(y)*outlier_ratio)
        if outlier_num != 0:
            # 使用paddle.randint生成服从均匀分布的、范围在[0, len(y))的随机Tensor
            outlier_idx = paddle.randint(len(y),shape = [outlier_num])
            y[outlier_idx] = y[outlier_idx] * 5
    return X, y

回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from matplotlib import pyplot as plt # matplotlib 是 Python 的绘图库

func = linear_func
interval = (-10,10)
train_num = 100 # 训练样本数目
test_num = 50 # 测试样本数目
noise = 2
X_train, y_train = create_toy_data(func=func, interval=interval, sample_num=train_num, noise = noise, add_outlier = False)
X_test, y_test = create_toy_data(func=func, interval=interval, sample_num=test_num, noise = noise, add_outlier = False)

X_train_large, y_train_large = create_toy_data(func=func, interval=interval, sample_num=5000, noise = noise, add_outlier = False)

# paddle.linspace返回一个Tensor，Tensor的值为在区间start和stop上均匀间隔的num个值，输出Tensor的长度为num
X_underlying = paddle.linspace(interval[0],interval[1],train_num) 
y_underlying = linear_func(X_underlying)

# 绘制数据
plt.scatter(X_train, y_train, marker='*', facecolor="none", edgecolor='#e4007f', s=50, label="train data")
plt.scatter(X_test, y_test, facecolor="none", edgecolor='#f19ec2', s=50, label="test data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"underlying distribution")
plt.legend(fontsize='x-large') # 给图像加图例
plt.savefig('ml-vis.pdf') # 保存图像到PDF文件中
plt.show()

image-20221018153352091

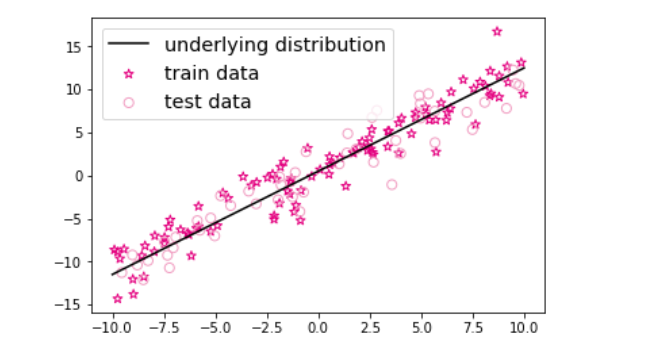
线性模型的构建

在线性回归中，自变量为样本的特征向量$\boldsymbol{x}\in \mathbb{R}^D$(每一维对应一个自变量)，因变量是连续值的标签$y\in R$。

线性模型定义为：
$$
f(\boldsymbol{x};\boldsymbol{w},b)=\boldsymbol{w}^T\boldsymbol{x}+b。 (2.6)
$$

其中权重向量$\boldsymbol{w}\in \mathbb{R}^D$和偏置$b\in \mathbb{R}$都是可学习的参数。

注意：《神经网络与深度学习》中为了表示的简洁性，使用增广权重向量来定义模型。而在本书中，为了和代码实现保持一致，我们使用非增广向量的形式来定义模型。

在实践中，为了提高预测样本的效率，我们通常会将$N$样本归为一组进行成批地预测，这样可以更好地利用GPU设备的并行计算能力。

$$
\boldsymbol{y} =\boldsymbol{X} \boldsymbol{w} + b, (2.7)
$$

其中$\boldsymbol{X}\in \mathbb{R}^{N\times D}$为$N$个样本的特征矩阵，$\boldsymbol{y}\in \mathbb{R}^N$为$N$个预测值组成的列向量。

注意：在实践中，样本的矩阵$\boldsymbol{X}$是由$N$个$\boldsymbol{x}$的行向量组成。而原教材中$\boldsymbol{x}$为列向量，其特征矩阵与本书中的特征矩阵刚好为转置关系。

线性算子

实现公式(2.7)中的线性函数非常简单，我们直接利用如下张量运算来实现。

1
2
3
4
5
# X: tensor, shape=[N,D]
# y_pred: tensor, shape=[N]
# w: shape=[D,1]
# b: shape=[1]
y_pred = paddle.matmul(X,w)+b
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
import paddle
import torch

torch.seed() #设置随机种子
class Op(object):
    def __init__(self):
        pass

    def __call__(self, inputs):
        return self.forward(inputs)

    def forward(self, inputs):
        raise NotImplementedError

    def backward(self, inputs):
        raise NotImplementedError

# 线性算子
class Linear(Op):
    def __init__(self, input_size):
        """
        输入：
           - input_size:模型要处理的数据特征向量长度
        """
		
        self.input_size = input_size

        # 模型参数
        self.params = {}
        # 行向量
        self.params['w'] = paddle.randn(shape=[self.input_size,1],dtype='float32')
        # self.params['w'] = torch.randn(self.input_size,1,dtype=torch.float32)
        1*1
        self.params['b'] = paddle.zeros(shape=[1],dtype='float32')
        # self.params['b'] = torch.zeros(1,dtype=torch.float32)

    def __call__(self, X):
        return self.forward(X)

    # 前向函数
    def forward(self, X):
        """
        输入：
           - X: tensor, shape=[N,D]
           注意这里的X矩阵是由N个x向量的转置拼接成的，与原教材行向量表示方式不一致
        输出：
           - y_pred： tensor, shape=[N]
        """

        N,D = X.shape

        if self.input_size==0:
            return paddle.full(shape=[N,1], fill_value=self.params['b'])
            # return torch.full(size=[N,1],fill_value=self.params['b'])
        
        assert D==self.input_size # 输入数据维度合法性验证

        # 使用paddle.matmul计算两个tensor的乘积
        y_pred = paddle.matmul(X,self.params['w'])+self.params['b']
        # y_pred = torch.matmul(X,self.params['w']+self.params['b'])
        
        return y_pred

# 注意这里我们为了和后面章节统一，这里的X矩阵是由N个x向量的转置拼接成的，与原教材行向量表示方式不一致
input_size = 3
N = 2
2*3
X = paddle.randn(shape=[N, input_size],dtype='float32') # 生成2个维度为3的数据

# X = torch.randn(N,input_size,dtype=torch.float32)
model = Linear(input_size)
y_pred = model(X)
print("y_pred:",y_pred) #输出结果的个数也是2个

损失函数

回归任务是对连续值的预测，希望模型能根据数据的特征输出一个连续值作为预测值。因此回归任务中常用的评估指标是均方误差。

令$\boldsymbol{y}\in \mathbb{R}^N$，$\hat{\boldsymbol{y}}\in \mathbb{R}^N$分别为$N$个样本的真实标签和预测标签，均方误差的定义为：

$$
\mathcal{L}(\boldsymbol{y},\hat{\boldsymbol{y}})=\frac{1}{2N}|\boldsymbol{y}-\hat{\boldsymbol{y}}|^2=\frac{1}{2N}|\boldsymbol{X}\boldsymbol{w}+\boldsymbol{b}-\boldsymbol{y}|^2, (2.8)
$$
其中$\boldsymbol{b}$为$N$维向量，所有元素取值都为$b$。

均方误差的代码实现如下:

注意：代码实现中没有除2。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import paddle
import torch

def mean_squared_error(y_true, y_pred):
    """
    输入：
       - y_true: tensor，样本真实标签
       - y_pred: tensor, 样本预测标签
    输出：
       - error: float，误差值
    """
    # 确定两者的维度一致
    assert y_true.shape[0] == y_pred.shape[0]
    
    # paddle.square计算输入的平方值
    # paddle.mean沿 axis 计算 x 的平均值，默认axis是None，则对输入的全部元素计算平均值。
    # error = paddle.mean(paddle.square(y_true - y_pred))
    error = torch.mean(torch.square(y_true-y_pred))
    return error


# 构造一个简单的样例进行测试:[N,1], N=2
# y_true = paddle.to_tensor([[-0.2],[4.9]],dtype='float32')
y_true = torch.tensor([[-0.2],[4.9]],dtype=torch.float32)
# y_pred = paddle.to_tensor([[1.3],[2.5]],dtype='float32')
y_pred = torch.tensor([[1.3],[2.5]],dtype=torch.float32)

error = mean_squared_error(y_true=y_true, y_pred=y_pred).item()
print("error:",error)

error: 4.005000114440918

2.2.4 模型优化

采用经验风险最小化，线性回归可以通过最小二乘法求出参数$\boldsymbol{w}$和$b$的解析解。计算公式(2.8)中均方误差对参数$b$的偏导数，得到
$$
\frac{\partial \mathcal{L}(\boldsymbol{y},\hat{\boldsymbol{y}})}{\partial b} = \mathbf{1}^T (\boldsymbol{X}\boldsymbol{w}+\boldsymbol{b}-\boldsymbol{y}), (2.9)
$$

其中$\mathbf{1}$为$N$维的全1向量。这里为了简单起见省略了均方误差的系数$\frac{1}{N}$，并不影响最后的结果。

令上式等于0，得到
$$
b^* =\bar{y}-\bar{\boldsymbol{x}}^T \boldsymbol{w},(2.10)
$$

其中$\bar{y} = \frac{1}{N}\mathbf{1}^T\boldsymbol{y}$为所有标签的平均值，$\bar{\boldsymbol{x}} = \frac{1}{N}(\mathbf{1}^T \boldsymbol{X})^T$ 为所有特征向量的平均值。将$b^*$代入公式(2.8)中均方误差对参数$\boldsymbol{w}$的偏导数，得到
$$
\frac{\partial \mathcal{L}(\boldsymbol{y},\hat{\boldsymbol{y}})}{\partial \boldsymbol{w}} = (\boldsymbol{X}-\bar{\boldsymbol{x}}^T)^T \Big((\boldsymbol{X}-\bar{\boldsymbol{x}}^T)\boldsymbol{w}-(\boldsymbol{y}-\bar{y})\Big).(2.11)
$$
令上式等于0，得到最优的参数为
$$
\boldsymbol{w}^*=\Big((\boldsymbol{X}-\bar{\boldsymbol{x}}^T)^T(\boldsymbol{X}-\bar{\boldsymbol{x}}^T)\Big)^{\mathrm{-}1}(\boldsymbol{X}-\bar{\boldsymbol{x}}^T)^T (\boldsymbol{y}-\bar{y}),(2.12)
$$

$$
b^* = \bar{y}-\bar{\boldsymbol{x}}^T \boldsymbol{w}^*.(2.13)
$$

若对参数$\boldsymbol{w}$加上$\ell_2$正则化，则最优的$\boldsymbol{w}^*$变为
$$
\boldsymbol{w}^*=\Big((\boldsymbol{X}-\bar{\boldsymbol{x}}^T)^T(\boldsymbol{X}-\bar{\boldsymbol{x}}^T)+\lambda \boldsymbol{I}\Big)^{\mathrm{-}1}(\boldsymbol{X}-\bar{\boldsymbol{x}}^T)^T (\boldsymbol{y}-\bar{y}),(2.14)
$$

其中$\lambda>0$为预先设置的正则化系数，$\boldsymbol{I}\in \mathbb{R}^{D\times D}$为单位矩阵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def optimizer_lsm(model, X, y, reg_lambda=0):
  """
    输入：
       - model: 模型
       - X: tensor, 特征数据，shape=[N,D]
       - y: tensor,标签数据，shape=[N]
       - reg_lambda: float, 正则化系数，默认为0
    输出：
       - model: 优化好的模型
    """

  N, D = X.shape

  # 对输入特征数据所有特征向量求平均
  x_bar_tran = paddle.mean(X,axis=0).T 
  
  # 求标签的均值,shape=[1]
  y_bar = paddle.mean(y)
  
  # paddle.subtract通过广播的方式实现矩阵减向量
  x_sub = paddle.subtract(X,x_bar_tran)

  # 使用paddle.all判断输入tensor是否全0
  if paddle.all(x_sub==0):
    model.params['b'] = y_bar
    model.params['w'] = paddle.zeros(shape=[D])
    return model
  
  # paddle.inverse求方阵的逆
  tmp = paddle.inverse(paddle.matmul(x_sub.T,x_sub)+
          reg_lambda*paddle.eye(num_rows = (D)))

  w = paddle.matmul(paddle.matmul(tmp,x_sub.T),(y-y_bar))
  
  b = y_bar-paddle.matmul(x_bar_tran,w)
  
  model.params['b'] = b
  model.params['w'] = paddle.squeeze(w,axis=-1)

  return model

input_size = 1
model = Linear(input_size)
model = optimizer_lsm(model,X_train.reshape([-1,1]),y_train.reshape([-1,1]))
print("w_pred:",model.params['w'].item(), "b_pred: ", model.params['b'].item())

y_train_pred = model(X_train.reshape([-1,1])).squeeze()
train_error = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()
print("train error: ",train_error)

w_pred: 1.1961743831634521 b_pred: 0.5631881952285767 train error: 3.670858144760132

模型评估

下面用训练好的模型预测一下测试集的标签，并计算在测试集上的损失。

1
2
3
y_test_pred = model(X_test.reshape([-1,1])).squeeze()
test_error = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()
print("test error: ",test_error)

test error: 4.327543258666992

实现多项式回归

多项式回归是回归任务的一种形式，其中自变量和因变量之间的关系是$M$次多项式的一种线性回归形式，即：
$$
f(\boldsymbol{x};\boldsymbol{w})=w_1x+w_2x^2+…+w_Mx^M+b=\boldsymbol{w}^T\phi(x)+b, （2.10）
$$
其中$M$为多项式的阶数，$\boldsymbol{w}=[w_1,…,w_M]^T$为多项式的系数，$\phi(x)=[x,x^2,\cdots,x^M]^T$为多项式基函数，将原始特征$x$映射为$M$维的向量。当$M=0$时，$f(\boldsymbol{x};\boldsymbol{w})=b$。

公式（2.10）展示的是特征维度为1的多项式表达，当特征维度大于1时，存在不同特征之间交互的情况，这是线性回归无法实现。公式（2.11）展示的是当特征维度为2，多项式阶数为2时的多项式回归：

$$
f(\boldsymbol{x};\boldsymbol{w})=w_1x_1+w_2x_2+w_3x_1^2+w_4x_1x_2+w_5x_2^2+b, （2.11）
$$

当自变量和因变量之间并不是线性关系时，我们可以定义非线性基函数对特征进行变换，从而可以使得线性回归算法实现非线性的曲线拟合。

接下来我们基于特征维度为1的自变量介绍多项式回归实验。

数据生成

假设我们要拟合的非线性函数为一个缩放后的$sin$函数。

学习笔记
#神经网络与深度学习
神经网络与深度学习实验二——机器学习基础
http://paopao0226.site/post/eb959071.html
作者
Ywj226
发布于
2022年10月16日
更新于
2023年9月23日
许可协议