前馈神经网络笔记
本文最后更新于:几秒前
《神经网络与机器学习》第四章笔记
激活函数
性质
- 连续可导(允许少数点不可导)的非线性函数
- 尽可能简单
- 导函数的值域在合理的范围内(防止梯度消失与梯度爆炸)
常见激活函数
1、$ \sigma(x) = {1 \over {1+exp(-x)}} \rightarrow tanh(x) = { {exp(x)-exp(-x)} \over {exp(x)+exp(-p)}} $
饱和函数,$tanh(x)$零中心化,$logistic$函数恒大于零。非零中心化的输出会使之后的输入发生偏置偏移,并进一步使得梯度下降的收敛速度变慢。
2、$ReLU(x)=\begin{cases} x & x \ge 0 \\\\ 0 & x \lt 0 \end{cases}$
$\rightarrow LeakyReLU(x)=\begin{cases} x & x \gt 0 \\\\ \gamma x & x \le 0 \end{cases}$
$\rightarrow ELU(x) = \begin{cases} x & x \gt 0 \\\\ \gamma (exp(x)-1) & x \le 0 \end{cases} = max(0,x)+max(0,\gamma (exp(x)-1))$
$softplus(x) = log(1+exp(x))$
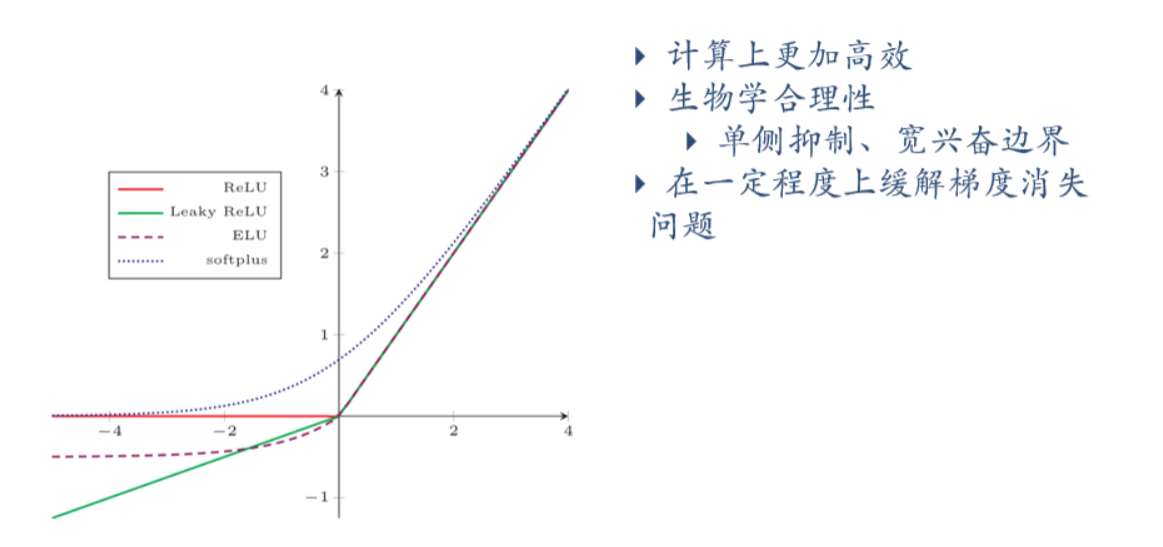
以上激活函数左侧不激活,右侧随信号提升而增大,在生物学上有着更高的合理性,因此目前使用$ReLU$系列激活函数的有很多
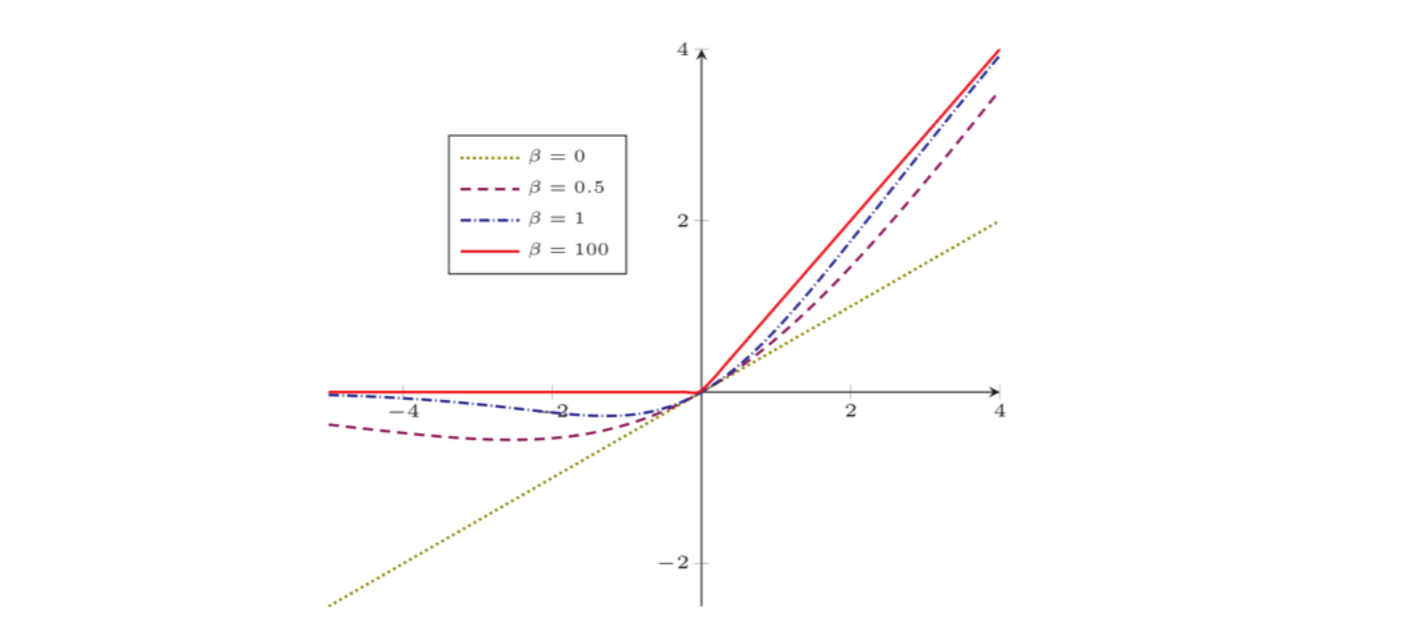
3、$Swish(x) = x\sigma(\beta x)$
一种软门控的激活函数,结合了第一种斜坡函数与第二种$sigmoid$函数,左半部分$x$作为斜坡函数,是主信号;右半部分$\sigma(\beta x)$是控制门,从[0,1]进行变化,等于0时信号完全关闭,等于1时信号放开。$Swish$函数的变化范围会随着$\beta$的变化而有差异。
总结

人工神经网络
三要素
神经元的激活规则、网络的拓扑结构、学习算法
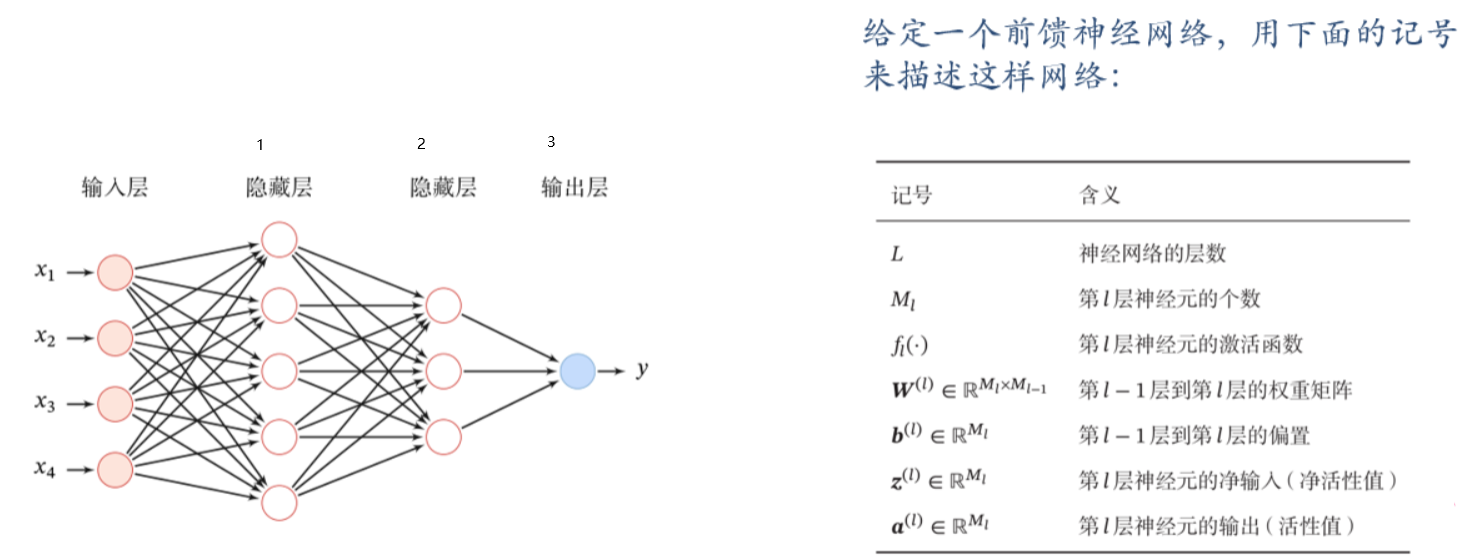
前馈神经网络(全连接神经网络、多层感知机)
各神经元分别属于不同的层,层内无连接,相邻两层之间的神经元全部两两连接,信号从输入层传播到输出层单向传播,无循环。
矩阵微积分
分母布局
标量关于向量的偏导数
$$
{\partial y\over \partial \pmb x} = [{\partial y \over \partial x_1 },{\partial y \over \partial x_2 },…,{\partial y \over \partial x_p} ]
$$向量关于向量的偏导数
$$
{\partial f(\pmb x) \over \partial \pmb x} =
\left[
\begin{matrix}
{\partial y_1 \over \partial x_1 } & … & {\partial y_q \over \partial x_1 } \\
\vdots & \vdots & \vdots \\
{\partial y_1 \over \partial x_p } & … & {\partial y_q \over \partial x_p } \\
\end{matrix}
\right]
\in \mathbb R^{p\times q}
$$
传播公式
$$
\begin{align}
\pmb z^{(l)} & = \pmb W^{(l)}\pmb a^{(l-1)}+\pmb b^{(l)} \\\
\pmb a^{(l)} & = f_l(\pmb z^{(l)})
\end{align}
$$
前馈计算
$$
\pmb x = \pmb a^{(0)} \rightarrow \pmb z^{(1)} \rightarrow \pmb a^{(1)} \rightarrow \pmb z^{(2)} \rightarrow … \rightarrow \pmb a^{(L-1)} \rightarrow \pmb z^{(L)} \rightarrow \pmb a^{(L)} = \phi (\pmb x;\pmb W,\pmb b)
$$
通用近似定理
对于具有线性输出层和至少一个使用”挤压“性质的激活函数的隐藏层组成的前馈神经网络,其可以以任意精度近似一个定义在实数空间的有限闭集函数,换言之,前馈神经网络在近似函数时是万能的。
反向传播
链式法则是在微积分中求复合函数的一种常见方法。
若$x \in \mathbb R,\pmb u=u(x) \in \mathbb R^s,\pmb g=g(\pmb u)\in \mathbb R^t$,则
$$
{\partial \pmb g \over \partial x}={\partial \pmb u \over \partial x}{\partial \pmb g \over \partial \pmb u} \in \mathbb R^{1\times t}
$$若$x \in \mathbb R^p,\pmb y=g(\pmb x) \in \mathbb R^s,\pmb z=f(\pmb y)\in \mathbb R^t$,则
$$
{\partial \pmb z \over \partial \pmb x}={\partial \pmb y \over \partial \pmb x}{\partial \pmb z \over \partial \pmb y} \in \mathbb R^{p \times t}
$$若$X\in \mathbb R^{p\times q}$为矩阵,$\pmb y=g(X) \in \mathbb R^s,z=f(\pmb y)\in \mathbb R$,则
$$
{\partial z\over \partial X_{ij}} = {\partial \pmb y \over {\partial X_{ij}}}{\partial z \over \partial \pmb y} \in \mathbb R
$$
以前向传播公式为例
$$
\begin{align}
\pmb z^{(l)} & = \pmb W^{(l)}\pmb a^{(l-1)}+\pmb b^{(l)} \\\
\pmb a^{(l)} & = f_l(\pmb z^{(l)})
\end{align}
$$
对其中的参数$W$和$b$求导可得
$$
{\partial \mathcal L(y,\hat y) \over \partial w^{(l)}_ {ij} }= {\partial \pmb z^{(l)} \over \partial w^{(l)}_ {ij}} {\partial \mathcal L (y, \hat y) \over \partial \pmb z^ {(l)} } \\\
{\partial \mathcal L(y,\hat y) \over \partial \pmb b^{(l)}_ {ij} }= {\partial \pmb z^{(l)} \over \partial \pmb b^{(l)}_ {ij}} {\partial \mathcal L (y, \hat y) \over \partial \pmb z^ {(l)} }
$$
若需要实现对前向传播过程,需要对参数的求导结果进行计算,根据链式法则得,可以从后到前执行计算。进一步,我们对参数求导公式的部分结果进行推导。
对于${\partial \pmb z^{(l)} \over \partial w^{(l)}_ {ij}}$,向量中只有一项与$w_{ij} ^{(l)}$有关
$$
\begin{align}
{\partial \pmb z^{(l)} \over \partial w^{(l)}_ {ij}} & = [{\partial z_1 ^{(l)} \over \partial w^{(l)}_ {ij}}, … , {\partial z_i ^{(l)} \over \partial w^{(l)}_ {ij}}, …, {\partial z_{m^{(l)}} ^{(l)} \over \partial w^{(l)}_ {ij}}] \\\
& = [\ 0, … ,{\partial (\pmb w_{i:} ^{(l)} \pmb a^{(l-1)})+b_i ^{(l)} \over \partial w_ {ij} ^{(l)}}, … , 0\ ] \\\
& = [\ 0, … , a_j^{(l-1)}, … , 0\ ] \\\
& = \mathbb I_i (a_j ^{(l-1)}) \in \mathbb R^ {m^ {(l)}}
\end{align}
$$
对于${\partial \pmb z^{(l)} \over \partial b^{(l)}}$,因为函数是一个线性函数,对于每一维的位置应该为1,因此结果应该为单位阵
$$
{\partial \pmb z^{(l)} \over \partial b^{(l)}} = \pmb I_ {m^{(l)}} \in \mathbb R^ {m^{(l)} \times m^{(l)}}
$$
对于$\delta^{(l)} = {\partial \mathcal L(\pmb {y,\hat y}) \over \partial \pmb z^{(l)}} \in \mathbb R^{m^{(l)}}$,根据
$$
\begin{align}
\pmb z^{(l)} & = \pmb W^{(l)}\pmb a^{(l-1)}+\pmb b^{(l)} \\\
\pmb a^{(l)} & = f_l(\pmb z^{(l)})
\end{align}
$$
有
$$
\begin{align}
\delta^{(l)} & = {\partial \mathcal L(\pmb {y,\hat y}) \over \partial \pmb z^{(l)}} \\\
& = {\partial \pmb a^ {(l)} \over \partial \pmb z^{(l)}}·{\partial \pmb z^ {(l+1)} \over \partial \pmb a^{(l)}}·{\partial \mathcal L(\pmb {y,\hat y}) \over \partial \pmb z^{(l+1)}} \\\
& = diag(f_l ^\prime (\pmb z^{(l)})) · (\pmb W^{(l+1)})^\top · \delta^{(l+1)} \\\
& = f_l ^\prime (\pmb z^{(l)}) \ \odot \ ((\pmb W^{(l+1)})^\top \delta^{(l+1)})
\end{align}
$$
在上式的结果中我们可以看到,$\delta^{(l)}$的结果和$\delta^{(l+1)}$有关,以此类推;其他部分可以通过计算得到。反向传播算法的原理就在这里,是通过后面的导数值向前推,从$\delta^{(L)}$向前推到$\delta^{(1)}$,从而计算出整个网络的导数值。
因此,对于$W$和$b$的求解可以写成以下形式:
$$
{\partial \mathcal L(\pmb {y,\hat y}) \over \partial w_{ij} ^{(l)}} = \mathbb I_i (a_j ^{(l-1)}) \delta^ {(l)} = \delta_i ^{l} a_j ^{(l-1)} \\\\
{\partial \mathcal L(\pmb {y,\hat y}) \over \partial \pmb b^ {(l)}} = \delta^{(l)}
$$
进一步的,$L(\pmb{y,\hat y})$关于第$l$层权重$W^{(l)}$的梯度为:
$$
{\partial \mathcal L(\pmb {y,\hat y}) \over \partial W ^{(l)}} = \mathbb I_i (a_j ^{(l-1)}) \delta^ {(l)} = \delta_i ^{l} (\pmb a ^{(l-1)})^\top
$$
反向传播算法的总体流程如下:

计算图与自动微分
自动微分是利用链式法则来自动计算一个复合函数的梯度的方法。
如以下的计算图:
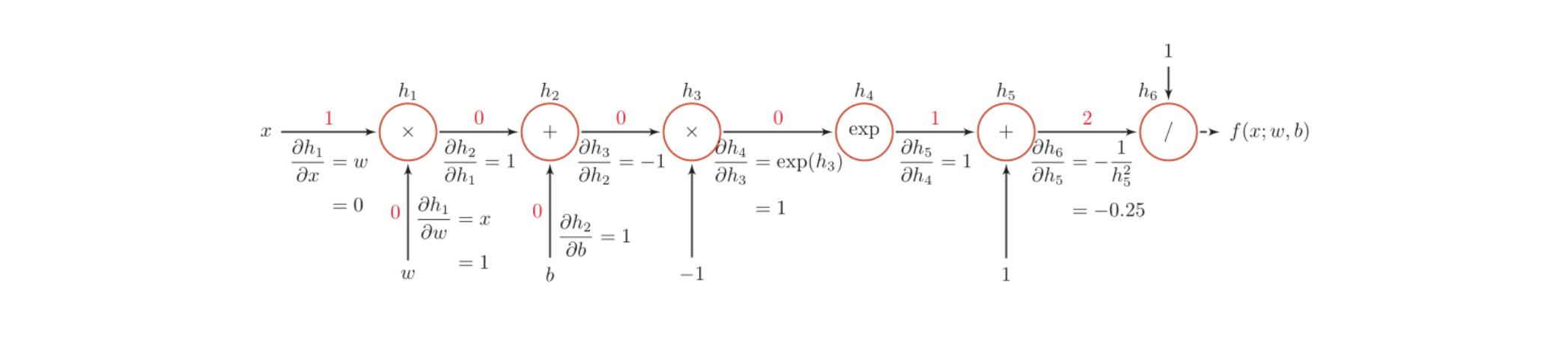
对于以上的计算图,我们可以从左到右分步完成每一步计算的导数值,然后链式求解。

当x=1,w=0,b=0时,可得
$$
\begin{align}
{\partial f(x;w,b)\over \partial w }|_{x=1,w=0,b=0} & = {\partial f(x;w,b)\over \partial h_6} {\partial h_6 \over \partial h_5}{\partial h_5 \over \partial h_4}{\partial h_4 \over \partial h_3}{\partial h_3 \over \partial h_2}{\partial h_2 \over \partial h_1}{\partial h_1 \over \partial w} \\\
& = 1 \times -0.25 \times 1 \times 1 \times -1 \times 1 \times 1 \\\
& = 0.25
\end{align}
$$
如果函数和参数之间有多条路径存在,可以将多条路径上的导数再进行相加,得到最终的梯度。
训练过程
- 前向计算每层的状态和激活值,直到最后一层
- 反向计算每一层的参数的偏导数
- 更新参数
计算图
分为静态计算图和动态计算图,静态图在编译时构建,动态图在运行时构建。
优化问题
- 参数过多,影响训练
- 非凸优化问题:即存在局部最优而非全局最优解,影响迭代
- 梯度消失问题:下层参数难调
- 参数解释问题