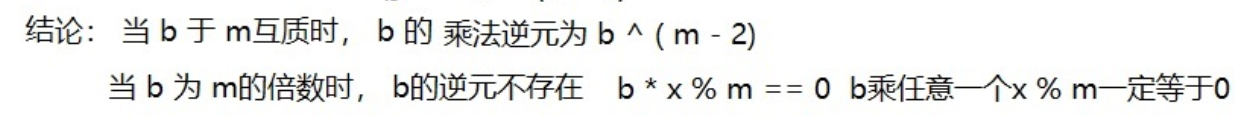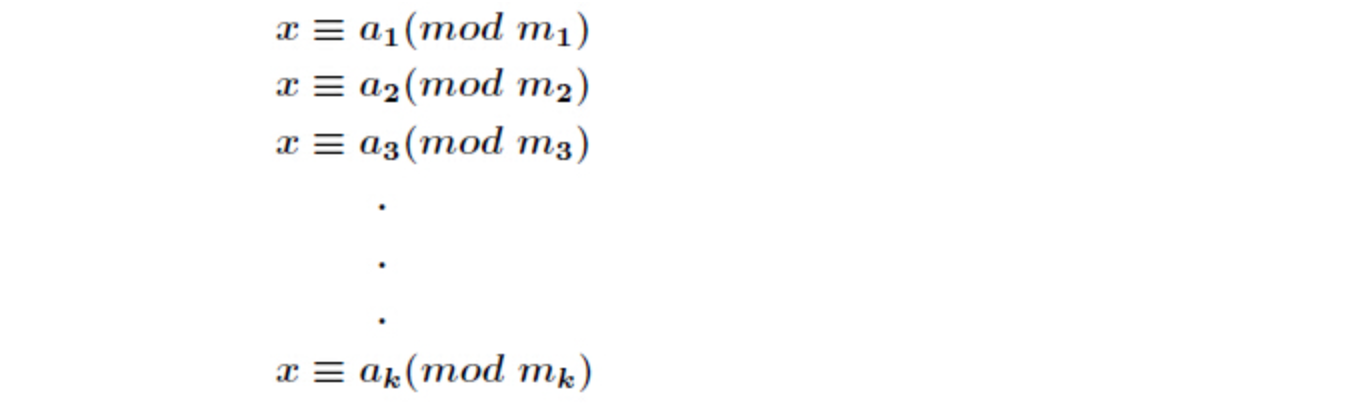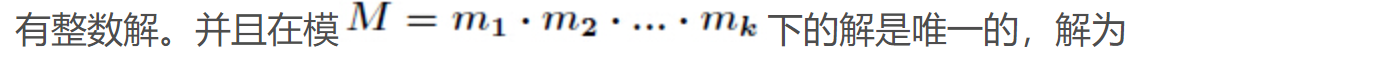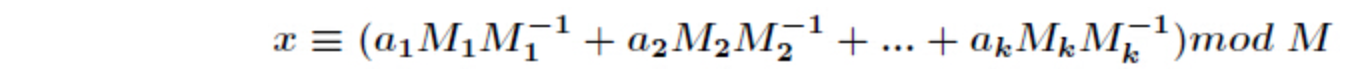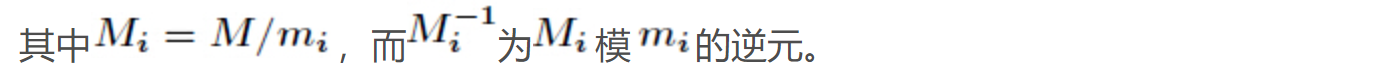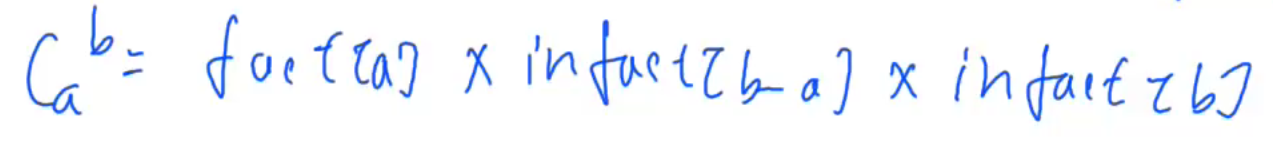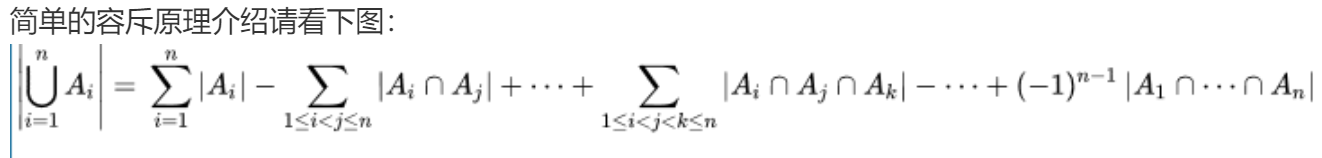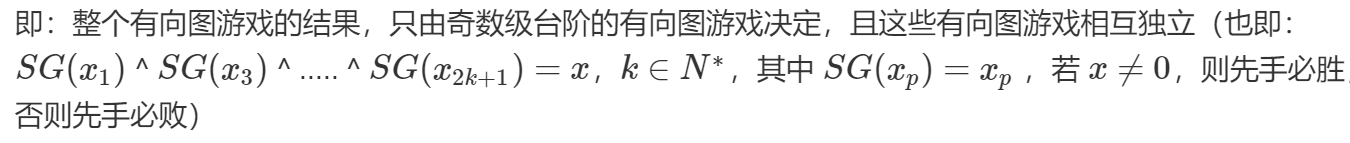机试复习

本文最后更新于：几秒前

SF

1、数组越界；2、数组开小了

快速排序

1、特判

2、取l,r为端点外边

3、循环(l<r)，使用do-while

4、递归调用，其中使用最后的r作为分割点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void quicksort(int num[],int left,int right){
    if(left >= right)return;
    //1、这里的l和r在外围，t是中间数，left+right-1的话，在分治的时候要用r作为边界点 
    int l = left-1;int r = right+1;int t = num[(left+right-1)/2];
    while(l < r){
        //2、先移动，后判断
        //移动左边	
        do l++; while(num[l] < t);
        //移动右边
        do r--; while(num[r] > t);
        //3、如果没有相遇，则交换l和r
        if(l < r){
            int tmp = num[l];
            num[l] = num[r];
            num[r] = tmp;
        }
    }
    //4、分治,r为分界点
    quicksort(num,left,r);
    quicksort(num,r+1,right);
}

归并排序

1、特判

2、先对两边sort

3、再对两边循环，merge

4、如果两段中有未完成循环的接到最后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
void mergesort(int num[],int l,int r){
    if(l >= r)return;
    int m = (l+r)/2;
    int tmp[r-l+1];
    //分治法将两端进行排序
    mergesort(num,l,m);	
    mergesort(num,m+1,r);
    //双指针将两端数组进行归并
    int i = l;int j = m+1;int k = 0;
    while(i <= m&&j <= r){
        if(num[i] < num[j]){
            tmp[k] = num[i];i++;
        }
        else{
            tmp[k] = num[j];j++;
        }
        k++;
    }
    //处理一段归并完成但另一段没有的情况
    while(i <= m){
        tmp[k] = num[i];i++;k++;
    }
    while(j <= r){
        tmp[k] = num[j];j++;k++;
    }
    k = 0;
    //赋值
    for(int a = l;a <= r;a++){
        num[a] = tmp[k];k++;
    }
}

二分排序

1、确定判断条件：如小于等于k的最大值

2、while(l<r){

​ int m = (l+r+1)/2; //取中点 ,如果有l=m则需取上分界

​ //小于等于：<=

​ if(f[m] <= k) l = m; //判断条件：我们需要找到最大值，因此需要尽量往右推，因为等于k的时候满足条件，所以右推的时候是l = m，不去除m对应的点防止丢失

​ else r = m+1;

}

1
2
3
4
5
6
7
8
9
10
11
12
13
int divide_right(int num[],int q,int l,int r){
    //右端点的特点是在右端点的左边的所有数都满足x <= q;
    while(l < r){
        //在这里需要取中点上界，防止死循环
        int m = (l+r+1)/2;
        //如果在右端点左边，说明x在num[m]和r之间，且可能num[m]==x;
        if(num[m] <= q) l = m;
        //否则m对应的数一定不在范围里，直接跳到下一个
        else r = m-1;
    }
    if(num[l] != q)return -1;
    return l;
}

浮点数二分

1
2
3
4
5
6
7
8
9
10
11
12
13
#include<iostream>
using namespace std;
int main(){
    double n;cin >> n;
    double l = -10000;double r = 10000;
    while(r-l > 1e-8){        
		double m = (l+r)/2;
        if(m * m * m >= n)r = m;       
		else l = m;
    }
    printf("%1f",l);
    return 0;
}

高精度计算(记成所有方法都要去除前导零)

加法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
首先**倒序**将各个数字存到vector里（使用a[i]-'0'）
然后对两个序列同时进行处理
vector<int> add(vector<int> a,vector<int> b){
    vector<int> r;
    int c = 0;
    int i = 0;
    //对两个序列进行迭代
    while(i < a.size() || i < b.size()){
        if(i < a.size()) c+=a[i];
        if(i < b.size()) c+=b[i];
        //结果位
        r.push_back(c%10);
        //值进位
        c = c/10;i++;
    }
    if(c) r.push_back(c);
    return r;
}

减法：

减法我觉得有一些些恶心

首先，减法的操作是用大数减小数，所以首先要判断一个两个数的大小

1
2
3
4
5
6
7
8
9
10
11
bool cmp(vector<int>a, vector<int> b){
    //如果a和b的size不同，返回长的
    if(a.size() != b.size()) return a.size() >= b.size();
    else {
        //从大位到小位判断，返回大的
        for(int i = a.size()-1;i >= 0;i--){
            if(a[i] != b[i])return a[i] > b[i];
        }
    }
    return true;
}

然后进行减法操作，操作如下：

1、设置一个t存储当前的借位，默认为0；

2、对两个序列a,b进行操作，注意借位

1
2
3
4
5
6
7
8
9
10
11
12
13
a-t-b,然后(t+10)%10判断是否借位
for(int i = 0;i < a.size();i++){
        //a大于b
        //减去借位
        t = a[i] - t;
    	//如果b还有，则减b
        if(i < b.size()) t -= b[i];
    	//加上借位
        r.push_back((t+10)%10);
    	//判断是否借位
        if(t<0) t = 1;
        else t = 0;
    }

3、去除前导0

1
while(r.size()>1 && r.back()==0) r.pop_back();

乘法

乘法的思路相对简单一些：

1、首先读入的值是一个vector和一个int，vector存高精度数

2、迭代的时候需要多迭代一次，即从0-size，因为到i==size的时候t可能有数字（超过现在的位数）

​ 思路：如果i<size，则当前位为(a[i]*b+t)%10，进位为(a[i] * b+t)/10；

3、去除前导零

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
	//多迭代一次
	for(int i = 0;i <= a.size();i++){
        if(i < a.size()){
            r.push_back((a[i]*b+t) % 10);
            t = (a[i]*b+t)/10;
        }
        else{
            r.push_back(t);
            t = 0;
        }
    }
    while(r.size() > 1 && r.back() == 0)r.pop_back();
    return r;


int t = 0;
for(int i = 0;i <= a.size();i++){
    if(i < a.size()){
        r.push_back((a[i]*b+t)%10);
        t = (a[i]*b+t)/10;
    }
    else{
        r.push_back(t);
        t = 0;
    }
}
while(r.size() > 1&&r.back()==0)r.pop_back();

除法

与前面不同，除法操作是从高位开始的，所以读入时需要注意从高位开始压入

存余数的话可以使用一个地址变量不断更新

除法的算法如下：

1、获取当前被除数值的大小 t = r*10+a[i];

2、获取结果与余数

​ 结果 res.push_back(t / b);

​ 余数 r = t%b;

使用int &r将余数返回到主函数

3、倒转结果

4、去除前导零

1
2
3
4
5
6
7
8
9
10
11
12
vector<int> div(vector<int> a,int b,int &r){
    vector<int> res;
    r = 0;
    for(int i = 0;i < a.size();i++){
        int t = r*10+a[i];
        res.push_back(t/b);
        r = t%b;
    }
    reverse(res.begin(),res.end());
    while(res.size() > 1&&res.back() == 0)res.pop_back();
    return res;
}

前缀和

一维前缀和

s[i] = a[i] + s[i-1]从1开始

求解[l,r] ：s[r]-s[l-1] //注意是l-1

二维前缀和

s[i,j] = s[i,j-1]+s[i-1,j] - s[i,j]+a[i,j];

求解[x1,y1] -> [x2,y2] ：s[x2,y2]-s[x1-1,y2]-s[x2,y1-1]+s[x1-1,y1-1] //注意x1-1,y1-1

差分

一维差分：求某一段的和

a[i] = s[i] - s[i-1];

求解在[l,r]范围+c：a[l] += c;a[r-1]-=c;

理解：对a[l]的操作在l之后的所有元素都产生影响

二维差分

1
2
3
4
5
6
void inv(int x1,int y1,int x2,int y2,int w){
    a[x1][y1] += w;
    a[x2+1][y1] -= w;
    a[x1][y2+1] -= w;
    a[x2+1][y2+1] += w;
}

步骤：

1、输入

2、inv(i,j,i,j,s[i,j]);

3、inv(x1,y1,x2,y2,w);

4、求和：a[i,j] += a[i,j-1]+a[i-1,j]-a[i-1,j-1];

双指针算法

板子：

1
2
3
4
5
6
7
8
9
//1、注意i,j的起始（从小到大/从大到小）
//2、check条件
for(int i = a,j = b;i <= n;i++){
    //dealing
    while(c[f[i]] > 1){
        c[f[j]]--;j++;
    }
 	//dealing
}

最长不连续子序列

快慢指针法：i指向右端点，j指向左端点

1
2
3
4
5
6
7
for(int i = 1,j = 1;i <= n;i++){
    c[f[i]]++;
    while(c[f[i]] > 1){
        c[f[j]]--;j++;
    }
    r = max(r,i-j+1);
}

数组元素的目标和

1
2
3
4
5
6
7
//从大到小
for(int i = 1,j = m-1;i <= n;i++){
    while(a[i]+b[j] > x) j--;
    if(a[i] + b[j] == x){
        cout << i << " " << j;break;
    }
}

判断子序列

1
2
3
4
5
6
for(int i = 1,j = 1;i <= n;i++){
    while(a[i] != b[j] && j<=m) j++;
    if(j <= m) {
        r++;j++;
    }
}

离散化

理解：将x,l,r单独压入一个vector，访问时只使用vector中的下标进行访问

如何找到对应index：使用二分查找

1、排序，模拟数轴

2、去重 all.erase(unique(all.begin(),all.end()),all.end());

1
2
3
//去重
sort(all.begin(),all.end());
all.erase(unique(all.begin(),all.end()),all.end());

3、对原位置的操作换成对二分之后的位置的操作

4、前缀

区间合并

1、按左边排序

2、两种判断情况：包含与交叉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//区间合并算法
vector<PII> merge(vector<PII> &a){
    vector<PII> res;
    //首先按照左边的位置进行排序
    sort(a.begin(),a.end());
    //保证第一个区间能够被正确处理，r<-1e9即可
    int l = -2e9;int r = -2e9;
    //针对包含、交叉、错位三种情况进行处理
    for(auto item:a){
        //错位的情况
        if(r < item.first){
            //如果不是第一次
            if(l != -2e9)res.push_back({l,r});
            l = item.first;
            r = item.second;
        }
        //包含与交叉的情况，左边因排序过，l一定是l，r取最大
        else r = max(r,item.second);
    }
    //处理最后一个区间
    if(l != -2e9)res.push_back({l,r});
    return res;
}

链表

单链表

e[idx] = b;ne[idx] = h[a];h[a] = idx++;

删除：ne[k] = ne[ne[k]];

双链表

初始化：r[0] = 1;r[1] = 0;idx=2;

传入左节点地址k和值x

e[idx] = x;r[idx] = r[k];l[idx] = k;l[r[k]] = idx;r[k] = idx;

删除中间结点k

r[l[k]] = r[k];

l[r[k]] = l[k];

艾海舟，孙立峰，袁春

模拟线性表

栈

数组模拟，top指针，从数组高位操作

表达式求值

1、建表

2、建计算

1
2
3
4
5
6
7
8
9
10
11
12
void eval(){
    char c = operators.top();operators.pop();
    int b = operant.top();operant.pop();
    int a = operant.top();operant.pop();
    switch(c){
        case '+' : operant.push(a+b);break;
        case '-' : operant.push(a-b);break;
        case '*' : operant.push(a*b);break;
        case '/' : operant.push(a/b);break;
        default:break;
    }
}

3、判断条件

①是数值 ②是左括号 ③是右括号 ④判断是否需要计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
if(isdigit(s[i])){
           int t = 0;
           while(isdigit(s[i])){
               t = t*10+s[i]-'0';i++;
           }
           i--;operant.push(t);
       }
       else if(s[i] == '(')operators.push('(');
       else if(s[i] == ')'){
           while(operators.top() != '('){
               eval();
           }
           operators.pop();
       }
       else{
           //注意这里：要先判断size()条件，每次都是这样，否则可能出现数组越界的问题
           while(operators.size() && p[operators.top()] >= p[s[i]]) eval();
           operators.push(s[i]);
       }

队列

数组模拟，双指针，从数组高位操作push，低位操作pop

单调栈与单调队列

单调栈：判断栈顶是否大于当前值即可

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

滑动窗口

注意！！！这道题用数组的单调队列做

对于每次操作的算法：

1、判断fr对应的值是否已经出栈

2、判断栈尾的值是否大于当前值，如果大于则栈尾的值一定不是最小值，出栈

3、将当前值压栈

4、输出栈顶值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
  	//初始fr == 0,rr == -1,让第一个数能直接入队
	for(int i = 0;i < n;i++){
        //首先判断最左边的点是否在窗口里
        if(fr <= rr && q[fr] < i-m+1) fr++;
        //其次判断是否大于栈尾，如果小于则压入，否则栈尾的元素一定不会是最小值，
        while(fr <= rr && f[q[rr]] >= f[i]) {
            rr--;
        }
        q[++rr] = i;
        if(i >= m-1) cout << f[q[fr]] << " " ;
    }

for(int i = 0;i < n;i++){
    if(fr<=rr && q[fr]<i-m+1)fr++;
    while(fr<=rr && f[q[rr]]>=f[i]) rr--;
    q[++rr] = i;
    if(i > m)cout << f[q[fr]] << " ";
}

KMP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
cin >> m >> p+1 >> n >> s+1;
//这里对p串的匹配从2开始是因为i==1时，i == j+1在开始一定是成立的，但是我们想要的是非平凡子串，ne[1] == 0，所以直接从2开始
for(int i = 2,j = 0;i <= n;i++){
    //当未匹配成功时则使用next向后跳跃
    while(j && p[i] != p[j+1]) j = ne[j];
    //判断是哪个条件跳出的，如果是i == j+1则匹配成功，j++指到下一个需要处理的位置；如果是j到头则不处理
    if(p[i] == p[j+1])j++;
    //对每个i的位置进行赋值。
    ne[i] = j;
}
//s串与p串的匹配，过程和next数组求解基本一致，不过next数组是p与p的匹配。
for(int i = 1,j = 0;i <= n;i++){
    while(j && s[i] != p[j+1]) j = ne[j];
    if(s[i] == p[j+1])j++;
    //判断是否整串完成匹配
    if(j == m){
        cout << i-m << " ";
        j = ne[j];
    }
}

Trie

//原理：使用一棵树来存储字符串

使用son[N,26]存储树，cnt[N]数组存每个位置的计数，对应不同的字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
int cnt[N],son[N][26],idx;

void insert(char s[]){
    int p = 0;
    for(int i=0;s[i];i++){
        //转义
        int t = s[i]-'a';
        //如果没有创建则创建
        if(!son[p][t]) son[p][t]=++idx;
        //下转
        p = son[p][t];
    }
    //计数增加
    cnt[p]++;
}

int query(char s[]){
    int p = 0;
    for(int i=0;s[i];i++){
        int t = s[i] - 'a';
        if(!son[p][t]) return 0;
        p = son[p][t];
    }
    return cnt[p];
}

void query(char s[]){
    int p = 0;
    for(int i = 0;s[i];i++){
        int t = s[i]-'a';
        if(!son[p][t])return 0;
        p = son[p][t];
    }
    return cnt[p];
}

最大异或对

原理：下溯的时候溯与当前位相反的数（保证异或最大）

注意：建树的时候从高到低

1
2
3
4
5
6
7
8
9
10
11
12
int query(int s){
    int r = 0,p = 0;
    for(int i = 30;i >= 0;i--){
        int t = s >> i & 1;
        if(son[p][!t]){
            r += 1 << i;
            p = son[p][!t];
        }
        else p = son[p][t];
    }
    return r;
}

并查集***

并查集可以用来进行集合处理

合并集合

1、首先将每个数做成一个集合

2、合并的时候将p[a] = b；

三种操作：注意这里找父节点用的是find函数
1、集合合并：p[find[a]] = find[b]
2、判断是否属于同一个集合：find[a] == find[b]
3、找到父节点：p[a] = find(p[a])

并查集操作：

1
2
3
4
5
int find(int x){
    //如果不是根节点，则一直上溯，上溯到的一定是根节点，然后在这条路上的所有点的父节点都变成根节点（路径压缩）
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}

连通块中点的数量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
if(s[0] == 'C'){
          cin >> a >> b;
          //注意这里：需要判定是否相等，否则会重复加
          if(find(a) != find(b)){
              cnt[find(b)] += cnt[find(a)];
              p[find(a)] = find(b);               
          }
      }
      else if(s[1] == '1'){
          cin >> a >> b;
          if(find(a)==find(b)) cout << "Yes" << endl;
          else cout << "No" << endl;
      }
      else if(s[1] == '2'){
          cin >> a;
          cout << cnt[find(a)] << endl;
      }

模拟堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
    if(!strcmp(op,"I")){
        int t;scanf("%d", &t);
        m++;s++;//这里的m出错了
        //尾部插入
        h[s] = t;
        hp[s] = m;ph[m] = s;
        //上处理，重新刷新堆
        up(s);
    }
    else if(!strcmp(op,"PM")){
        cout << h[1] << endl;
    }
    else if(!strcmp(op,"DM")){
        heap_swap(1,s);
        s--;down(1);
    }


void up(int x){
    while(x/2 > 0 && h[x/2] > h[x]) swap(h[x/2],h[x]);
    x /= 2;
}
void down(int x){
    int t = x;
    if(2*x<=s && h[2*x] < h[t]) t = 2*x;
    if(2*x+1 <=s&& h[2*x+1] < h[t]) t = 2*x+1;
    if(t != x){
        //这里使用的是下标，不是h！！！！！！！！！！！！
        heap_swap(t,x);
        down(t);
    }
}

模拟哈希

拉链法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
//求质数
const int N = 100003;
//开槽
int h[N],e[N],ne[N],idx;
void insert(int x){
	//转成正数
	int k = (x%N+N)%N;
	e[idx] = x;
	ne[idx] = h[k];
	h[k] = idx++;
}
int find(int x){
	int k = (x%N+N)%N;
	for(int i = h[k];i != -1;i = ne[i]){
		if(e[i] == x) return 1;
	}
	return 0;
}
int main(){
	注意要把槽设为-1
    int k = (x%N+N)%N;
	memset(h,-1,sizeof h);
}

字符串哈希

image-20210822154642276

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
//P = 131或13331
const int N = 100010;
const int P = 131;

typedef unsigned long long ULL; 

//h[i]:存1~i位置对应的哈希。p[i]:存第i位对应的p值。
int h[N],p[N];

ULL get(int l,int r){
    //h[r]:1~r;h[l-1]:1~l-1;
    //p[r-l+1]:对齐高位（ABCDE-ABC00 = DE）
    return h[r] - h[l-1] * p[r-l+1];
}

int main(){
	//从h[1]开始存储数字，代表前1个字符的哈希值，h[0]=0;
	//p[0]=1代表开始的时候没有指数增长。
    h[0] = 0;p[0] = 1;
    
    for(int i = 1;i <= n;i++) {
        cin >> str[i];
        //字符串的高位同样也是哈希的高位
        //h = h*p+str[i]
        h[i] = h[i-1] * P + str[i];
        //p指数增长
        p[i] = p[i-1] * P;
    }
    
    while(m--){
        int l1,r1,l2,r2;
        cin >> l1 >> r1 >> l2 >> r2;
        if(get(l1,r1) == get(l2,r2)) cout << "Yes" << endl;
        else cout << "No" << endl;
    }
    return 0;
}

DFS

排列数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//s[N]:存储是否使用，p[N]:按序存储DFS结果
int n,s[N],p[N];
void DFS(int u){
    if(u > n){
        for(int i = 1;i <= n;i++){
            cout << p[i] << " ";
        }
        cout << endl;
    }
    for(int i = 1;i <= n;i++){
        if(s[i] == 0){
            s[i] = u;
            p[u] = i;
            DFS(u+1);
            //恢复现场
            p[u] = 0;
            s[i] = 0;
        }
    }
}
int main(){
    cin >> n;
    DFS(1);
    return 0;
}

N皇后

只记迭代每个位置的方法

image-20210822213659047

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void DFS(int r,int c,int t){
    if(c > n){
        c = 1;
        r++;
    }
    if(r > n){
        if(t == n){
            for(int i = 1;i <= n;i++){
                for(int j = 1;j <= n;j++){
                    cout << s[i][j];
                }
                cout << endl;
            }
            cout<<endl;
        }
        return;
    }
    //注意这里先走不放棋子的分支
    //注意！！！！！！！！！！
    DFS(r,c+1,t);
    //判断横竖，对角线次对角线有没有被占
    if(!row[r] && !col[c] && !dg[r+c] && !udg[c-r+n]){
        row[r] = col[c] = dg[r+c] = udg[c-r+n] = 1;
        s[r][c] = 'Q';
        DFS(r,c+1,t+1);
        row[r] = col[c] = dg[r+c] = udg[c-r+n] = 0;
        s[r][c] = '.';
    }
}

BFS

走迷宫

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<iostream>
#include<queue>
#include<cstring>
#include<unordered_map>

using namespace std;
const int N = 110,M = 110;
typedef pair<int,int> MM;

int n,m;
int h[N][M];
//d表示与起点的距离
int d[N][M];
//偏移数组
int dx[4]={0,-1,0,1};
int dy[4]={1,0,-1,0};
queue<MM> q;
//在一个队列里完成层次遍历，直到队列再次为空，队列中先访问的点的距离一定是相对小的
void BFS(){
    //首先初始化d，所有点都没有走到
    memset(d,-1,sizeof d);
    //从(1,1)开始
    d[1][1]=0;
    while(!q.empty()){
        //首先判断是否到终点
        int x = q.front().first;
        int y = q.front().second;
        q.pop();
        //如果到终点则跳出
        if(x == n && y == m){
            cout << d[n][m];
            break;
        }
        //否则按照四周进行移动
        else{
            for(int i = 0;i < 4;i++){
                int px = x+dx[i];
                int py = y+dy[i];
                //判断是否是有效位置
                if(px > 0 && px <= n && py > 0 && py <= m && h[px][py] != 1 && d[px][py]== -1){
                    d[px][py] = d[x][y]+1;
                    q.push({px,py});
                }
            }
        }
    }
}

int main(){
    cin >> n >> m;
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= m;j++){
            cin >> h[i][j];
        }
    }
    q.push({1,1});BFS();
    return 0;
}

八数码

特征：矩阵移动性

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
void bfs(string s){
    string e = "12345678x";
    //入队
    q.push(s);
    //从初始串的位置开始
    d[s] = 0;
    //偏移向量
    int dx[4] = {1,-1,0,0};
    int dy[4] = {0,0,1,-1};
    //推理
    while(!q.empty()){、
        //出队
        string t = q.front();
        q.pop();
        //判断当前位置是否已经是结果
        int dt = d[t];
        if(t == e) {
            break;
        }
        //找到X的位置
        int xx = t.find('x');
        //转化为二维坐标
        int tx = xx / 3;
        int ty = xx % 3;
        //推理到四周的位置
        for(int i = 0;i < 4;i++){
            int px = tx + dx[i];
            int py = ty + dy[i];
            //如果是合法位置
            if(px >= 0 && px < 3 && py >= 0 && py < 3){
                //交换当前位置
                int dp = d[t]+1;
                swap(t[px*3+py],t[xx]);
                //如果这个情况没有被走过
                if(!d.count(t)){
                    d[t] = dp;
                    q.push(t);
                }
                //恢复现场
                swap(t[px*3+py],t[xx]);
            }
        }
    }
    //判断最终情况是否有记录
    if(d.count(e)) cout << d[e];
    else cout << -1;
}

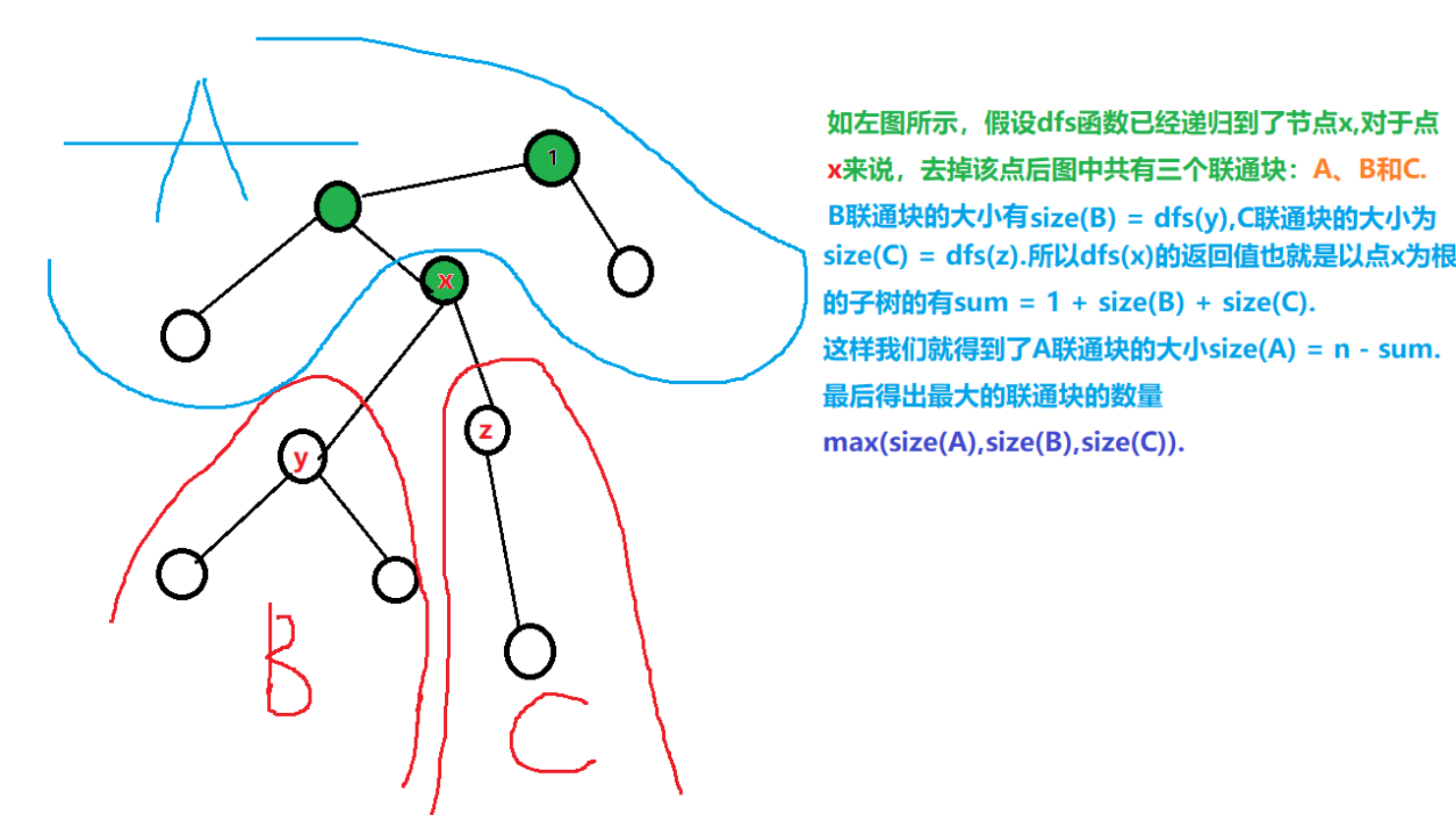
树与图的深度优先遍历

树的重心

image-20210823235144263

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//返回以u为根的子树中节点的个数，包括u节点
int dfs(int u) {
    int res = 0; //存储删掉某个节点之后，最大的连通子图节点数
    st[u] = true; //标记访问过u节点
    int sum = 1; //存储 以u为根的树的节点数, 包括u，如图中的4号节点
    //访问u的每个子节点
    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];
        //因为每个节点的编号都是不一样的，所以 用编号为下标来标记是否被访问过
        if (!st[j]) {
            int s = dfs(j);  // u节点的单棵子树节点数如图中的size值
            res = max(res, s); // 记录最大联通子图的节点数
            sum += s; //以j为根的树的节点数
        }
    }

    //n-sum 如图中的n-size值，不包括根节点4；
    res = max(res, n - sum); // 选择u节点为重心，最大的连通子图节点数
    ans = min(res, ans); //遍历过的假设重心中，最小的最大联通子图的节点数
    return sum;
}

树与图的广度优先遍历

图中点的层次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void bfs(){
    memset(d,-1,sizeof d);
    d[1] = 0;
    q.push(1);
    while(q.size()){
        int t = q.front();
        q.pop();
        for(int i = h[t];i != -1;i = ne[i]){
            if(d[e[i]] == -1){
                d[e[i]]=d[t]+1;
                q.push(e[i]);
            }
        }
        if(t == n){
            cout << d[t];return;
        }
    }
    cout << -1;
}

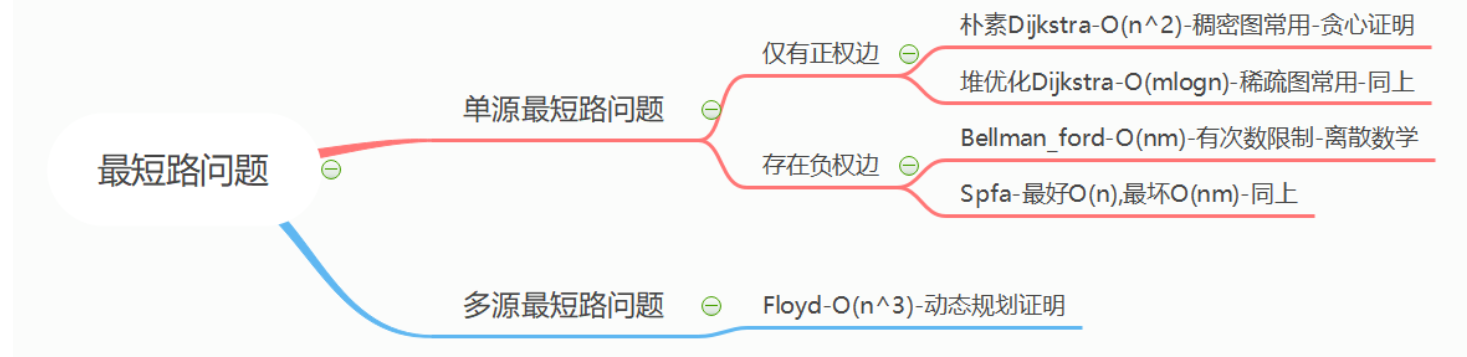
图的排序与最短路

拓扑排序

image-20210824144744931

注意：图中可能存在重边和自环

策略：宽搜+入度计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//先建图，记录入度
while(m--){
    int a,b;
    cin >> a >> b;
    add(a,b);
    //用一个d数组记入度
    d[b]++;
}
//然后从入度为0的点开始进行处理
//宽搜
bool topsort(){
   int count = 0;
   //首先找到所有入度为0的点
   for(int i = 1;i <= n;i++){
       if(d[i] == 0)q.push(i);
   }
   //宽搜
   while(q.size()){
       int tmp = q.front();
       q.pop();count++;
       res.push_back(tmp);
       for(int i = h[tmp];i != -1;i = ne[i]){
           int link = e[i];
           d[link]--;
           if(d[link] == 0)q.push(link);
       }
   }
   //如果所有点都走完了，这个图的拓扑序列有效
   if(count == n)return true;
   else return false;
}

image-20210825001507160

Dijkstra算法：非负权，有自环重边

Dijkstra 的整体思路比较清晰
即进行n（n为n的个数）次迭代去确定每个点到起点的最小值，最后输出的终点的即为我们要找的最短路的距离

步骤

迭代n次，每次迭代都找到一个符合条件的点加入，确定一个点的最短路的值，符合的条件为：

1、没有被处理过（即没有加入当前的连通分量）

2、距离最短

找到j点之后将use数组置1，然后对于所有和j点相连的点更新最短路。

初始化memset时无限大是0x3f,memset是按字节填充 int 4 个字节，判断的时候所以是0x3f3f3f3f

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//稠密图需要使用邻接矩阵存储图
int g[N][N];
//记录1点与其他点的距离
int dist[N];
//判断是否使用过
int use[N];
int n,m;

int dijkstr(){
    memset(dist,0x3f,sizeof dist);
    memset(use,0,sizeof use);
    //从1号点开始，所以dist[1] = 0;
    dist[1] = 0;
    //迭代所有点
    for(int i = 1;i <= n;i++){
        //设置一个t = -1，保证至少有一个点需要用到
        int t = -1;
        //判断当前点是否是有效点（未被用过的最短距离）
        for(int j = 1;j <= n;j++){
            if(!use[j] && (t == -1 || dist[t] > dist[j])) t = j;
        }
        //使用当前的点
        use[t] = 1;
        //更新从当前点到其他点的最小值
        for(int j = 1;j <= n;j++){
            if(dist[j] > dist[t]+g[t][j]){
                dist[j] = dist[t]+g[t][j];
            }
        }
    }
    //如果更新到了n，则现在的n所存的就是最短路值
    if(dist[n] != 0x3f3f3f3f) return dist[n];
    return -1;
}

int main(){
    //默认无穷大，即没有边
    memset(g,0x3f,sizeof g);
    cin >> n >> m;
    int a,b,w;
    while(m--){
        cin >> a >> b >> w;
        //注意这里只保存最短边
        g[a][b] = min(g[a][b],w);
    }
    int r = dijkstr();
    cout << r;
    return 0;
}

堆优化Dijkstra

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int disj(){
    memset(dist,0x3f,sizeof dist);
    q.push({0,1});
    while(!q.empty()){
        auto t = q.top();q.pop();
        int d = t.first;
        int v = t.second;
        //优先处理的是最短路，所以如果碰到了第二个相同点的距离，则该距离一定是大的，因此直接continue即可。
        if(use[v])continue;
        use[v] = true;
        // cout << d << "  " << v << endl;
        for(int i = h[v];i != -1;i = ne[i]){
            int k = e[i];
            //重新压入
            if(dist[k] > d+w[i]){
                q.push({d+w[i],k});
                dist[k] = d+w[i];
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

贝尔曼算法：含负权，有重边自环，图中可能 存在负权回路 。

步骤：

如果限制最短路上只有k条边，则最外层迭代k次，内层迭代m（边数）次，然后对每个边{a,b,w}，判断dist[b] = min(dist[b],dist[a]+w)，即松弛操作。

由于在代码中前面的操作可能会影响后面的操作，因此需要先保存上一次的处理结果，即对dist数组进行备份（注意语法）

image-20210824165312352

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
//所有边使用结构体存更方便
struct edge{
    int a,b,w;
} e[N];
int n,m,k;
int dist[N],backup[N];
int bellman_ford(){
    //首先设置所有点的距离为0x3f(无限大)
    memset(dist,0x3f,sizeof dist);
    //从1开始
    dist[1] = 0;
    //因为最多不经过k条边，因此迭代k次
    for(int i = 0;i < k;i++){
        //备份，防止出现串联现象,注意这个语法
        memcpy(backup,dist,sizeof dist);
        //每次对所有边进行迭代
        for(int j = 0;j < m;j++){
            int a = e[j].a;
            int b = e[j].b;
            int w = e[j].w;
            //松弛操作，判断三角不等式
            dist[b] = min(dist[b],backup[a]+w);
        }
    }
    //由于含有负权，因此在处理最短路的时候dist可能会小于0x3f，但是仍然是无限大的值，因此除以2
    if(dist[n] > 0x3f3f3f3f/2) return 0x3f;
    else return dist[n];
}

int main(){
    cin >> n >> m >> k;
    int i = 0;
    for(int i = 0;i < m;i++){
        int a,b,w;
        cin >> a >> b >> w;
        //注意结构体赋值操作
        e[i] = {a,b,w};
    }
    int r = bellman_ford();
    if(r == 0x3f)cout << "impossible";
    else cout << r;
    return 0;
}

spfa算法：含负权，可能存在重边和自环，判断是否有负环

求最短路

spfa是根据贝尔曼算法所做的优化，Bellman_ford算法会遍历所有的边，但是有很多的边遍历了其实没有什么意义，我们只用遍历那些到源点距离变小的点所连接的边即可，只有当一个点的前驱结点更新了，该节点才会得到更新；因此考虑到这一点，我们将创建一个队列每一次加入距离被更新的结点。

值得注意的是

1) st数组的作用：判断当前的点是否已经加入到队列当中了；已经加入队列的结点就不需要反复的把该点加入到队列中了，就算此次还是会更新到源点的距离，那只用更新一下数值而不用加入到队列当中。
即便不使用st数组最终也没有什么关系，但是使用的好处在于可以提升效率。

  1. SPFA算法看上去和Dijstra算法长得有一些像但是其中的意义还是相差甚远的:

Dijkstra算法里使用的是优先队列保存的是当前未确定最小距离的点，目的是快速的取出当前到源点距离最小的点；SPFA算法中使用的是队列(你也可以使用别的数据结构),目的只是记录一下当前发生过更新的点。

  1. ⭐️Bellman_ford算法里最后return-1的判断条件写的是dist[n]>0x3f3f3f3f/2;而spfa算法写的是dist[n]==0x3f3f3f3f;其原因在于Bellman_ford算法会遍历所有的边，因此不管是不是和源点连通的边它都会得到更新；但是SPFA算法不一样，它相当于采用了BFS，因此遍历到的结点都是与源点连通的，因此如果你要求的n和源点不连通，它不会得到更新，还是保持的0x3f3f3f3f。

  2. ⭐️ Bellman_ford算法可以存在负权回路，是因为其循环的次数是有限制的因此最终不会发生死循环；但是SPFA算法不可以，由于用了队列来存储，只要发生了更新就会不断的入队，因此假如有负权回路请你不要用SPFA否则会死循环。

  3. ⭐️求负环一般使用SPFA算法，方法是用一个cnt数组记录每个点到源点的边数，一个点被更新一次就+1，一旦有点的边数达到了n那就证明存在了负环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//距离,st存储点是否在队列中，队列每个点只需要存储一个（注意一下）
int d[N],st[N];
//队列
queue<int> q;
void add(int a,int b,int c){
    e[idx] = b;w[idx] = c;ne[idx] = h[a];h[a] = idx++;
}
int spfa(){
    //使用宽搜的方法来优化贝尔曼算法,注意初始化是用0x3f初始化
    memset(d,0x3f,sizeof d);
    //初始化
    d[1]=0;
    //从1点开始
    q.push(1);
    //当前点入队
    st[1] = 1;
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        //判断t点所连的边是否有更新
        for(int i = h[t];i != -1;i = ne[i]){
            int et = e[i];
            int wt = w[i];
            //spfa算法认为只有在当前被修改小之后的点才会影响之后连接的点,使其越来越小
            if(d[et] > d[t]+wt){
                //更新距离
                d[et] = d[t]+wt;
                //如果当前点没有入队
                if(!st[et]){
                    q.push(et);
                    st[et] = 1;
                }
            }
        }
    }
    if(d[n] == 0x3f3f3f3f)return -1;
    return d[n];
}

求负环（最常用）

1、初始的时候将所有点入队，因为负权回路可能是从任意一个点开始

2、在更新点的时候设置一个cnt数组存储x点到虚拟源点最短路的边数，初始每个点到虚拟源点的距离为0，只要他能再走n步，即cnt[x] >= n，则表示该图中一定存在负环，由于从虚拟源点到x至少经过n条边时，则说明图中至少有n + 1个点，表示一定有点是重复使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int spfa(){
    memset(d,0x3f,sizeof d);
    //需要设置一个位置开始迭代,因为1是最开始存进去的,所以先初始化d
    d[1] = 0;
    //将所有点加入队列
    for(int i = 1;i <= n;i++){
        q.push(i);st[i] = 1;
    }
    while(q.size()){
        int t = q.front();q.pop();
        st[t] = 0;
        for(int i = h[t];i != -1;i = ne[i]){
            int et = e[i];
            int wt = w[i];
            if(d[et] > d[t] + wt){
                d[et] = d[t] + wt;
                //更新cnt
                cnt[et] = cnt[t]+1;
                if(!st[et]){
                    q.push(et);
                    st[et] = 1;
                }
            }
            //抽屉原理判断负环
            if(cnt[et] >= n) return true;
        }
    }
    return false;
}

Floyd算法：多源最短路

三层循环，原理是dp

1
2
3
4
5
6
7
8
9
void floyd(){
    for(int a = 1;a <= n;a++){
        for(int b = 1;b <= n;b++){
            for(int c = 1;c <= n;c++){
                d[b][c] = min(d[b][c],d[b][a]+d[a][c]);
            }
        }
    }
}

注意使用邻接矩阵处理含重边和自环的图时需要进行预处理

重边：d[a,b] = min(d[a,b],w)

自环（默认自环为0）：d[a,a] = 0；

1
2
3
4
5
6
7
8
9
for(int i = 1; i <= n; i++)
     for(int j = 1; j <= n; j++)
         if(i == j) d[i][j] = 0;
         else d[i][j] = INF;
 while(m--) {
     cin >> x >> y >> z;
     d[x][y] = min(d[x][y], z);
     //注意保存最小的边
 }

图的处理总结

image-20210825001903536

最小生成树

prim算法

和dijkstra算法十分像。

联系：Dijkstra算法是更新到起始点的距离，Prim是更新到集合S的距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
int prim(){
    //初始化距离
    memset(d,0x3f,sizeof d);
    //不妨从1开始
    //注意这里不要st[1],让循环能选到1进行
    d[1] = 0;
    //结果
    int r = 0;
    for(int i = 0;i < n;i++){
        int t = -1;
        //找到最近点
        for(int j = 1;j <= n;j++){
            if(!st[j] && (t==-1 || d[t] > d[j])){
                t = j;
            }
        }
        //不同点1:判断是否连通,注意这里需要特判i,防止最开始的时候没有可连通的点
        if(d[t] == INF) return INF;
        r += d[t];
        st[t] = 1;      
        //更新其他点的距离
        for(int j = 1;j <= n;j++){
            //不同点2:距离更新的时候是更新和当前连通子图的距离,不是和虚拟源点的距离
            d[j] = min(d[j],g[t][j]);
        }
    }
    return r;
}

Kruskal算法

1、对边按照权值从小到大排序
2、迭代所有边，判断是否边的两端连通，如果不连通则将该边加入
3、判断条件：所有点已经加入（count）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
int p[N];
struct Edge{
    int a,b,w;
}e[N];
bool cmp(const Edge& a,const Edge&b){
    return a.w < b.w;
}
int find(int a){
    if(p[a]!=a) p[a] = find(p[a]);
    return p[a];
}


//初始化并查集
for(int i = 1;i <= n;i++)p[i] = i;
for(int i = 0;i < m;i++){
    int a,b,w;
    cin >> a >> b >> w;
    e[i] = {a,b,w};
}
//1、边排序
sort(e,e+m,cmp);
//2、从小到大判断是否两端连通
for(int i = 0;i < m;i++){
    int a = e[i].a;
    int b = e[i].b;
    int w = e[i].w;
    if(find(a) != find(b)){
        p[find(a)] = find(b);
        r+=w;
        cnt++;
    }
}
//3、判断是否是最小生成树
if(cnt == n)cout << r;
else cout << "impossible";

染色法判定二分图

image-20210825124328622

image-20210825124536399

遍历所有点，对于每个点为起点进行dfs。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
bool j = true;
//保证每个点都能作为起始染色点
for(int i = 1;i <= n;i++){
    //如果没有染色
    if(!color[i]){
        //如果从i开始染1号点不成功
        if(!dfs(i,1)) {
            j = false;
            break;
        }
    }
}
bool dfs(int k,int c){
	//先染色
    color[k] = c;
    //对连接的所有边判断情况是否成立
    for(int i = h[k];i!=-1;i = ne[i]){
        //两种情况
        if(color[e[i]] == 0){
            if(!dfs(e[i],3-c))return false;
        }
        else if(color[e[i]]==c)return false;
    }
    return true;
}


匈牙利算法判断二分图的最大匹配

image-20210825133131114

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
int g[N][N];
//st用于判断当前考虑到了哪个点
int st[N];
//match用于判断当前右边的点是否已有对应
int match[N];

bool find(int x){
    for(int i = 1;i <= n2;i++){
        if(!st[i] && g[x][i]){
            //注意这里
            //st数组用来保证本次匹配过程中，第二个集合中的每个点只被遍历一次，防止死循环。
            st[i] = true;
            //两种情况：第一种是右边的点空匹配，则匹配该点；第二种是右边的点匹配到的左边的点还有别的点可以匹配，则也可以匹配该点
            if(!match[i] || find(match[i])){
                match[i] = x;
                return true;
            }
        }
    }
    return false;
}
或
bool find(int a){
    //对a所连接的边进行迭代
    for(int i = h[a];i != -1;i = ne[i]){
        int et = e[i];
        if(!st[et]){
            st[et] = true;
            if(!match[et] || find(match[et])){
                match[et] = a;
                return true;
            }
        }
    }
    return false;
    
}

质数求解

试除法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//试除法是对定义的应用
/*
            两个条件：
            1、m是1，则No
            2、m是2，则判断从2到根号n是否有可以整除的数字
                原理：若d|n,则(n/d)|n 
        */
if(m<2) {
    cout << "No" << endl;continue;
}
//这里注意一下i <= m/i，只能用这种，i*i<=m有溢出风险，i<=sqrt(m)太慢
for(int i = 2;i <= m/i;i++){
    if(m % i == 0){
        cout << "No" << endl;
        k=0;break;
    }
}
if(k)cout << "Yes" << endl;

筛质数

埃式筛法

1
2
3
4
5
6
7
8
9
10
11
12
//埃式筛法
    int c= 0;
    //从2开始筛
    for(int i = 2;i <= n;i++){
        if(!st[i]){
            c++;
            for(int j = i;j <= n;j+=i){
                st[j] = 1;
            }
        }
    }

线性筛法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//线性筛法:拿质数筛质数
for(int i = 2;i <= n;i++){
    //找到质数
    if(!st[i]){
         //假设primes[0]为n最小的质因子,i为最大的因数，
        //易知若primes[i]中i>0,则会进入循环后产生多余的标记
        p[c++] = i;
        st[i] = 1;
    }
    //以当前质数为因子，之前的质数为另一个因子，筛数，质数*质数一定是不一样的
    for(int j = 0;p[j] <= n/i;j++){            
        //标记;primes[j]一定是primes[j]*i的最小质因子
        st[p[j]*i] = 1;
        //表明primes[j]一定是i的最小质因子,没有必要再遍历,primes要小于等于i的最小质因子
        //这样能保证每个数遍历一遍,而没有重复
        if(i % p[j] == 0)break;
    }
}
for(int i = 2;i <= n;i++){
    if(!st[i]){
        st[i]=1;
        prime[cnt++] =i;
        for(int j = 0;prime[j]<=n/i;j++){
            st[prime[j]*i]=1;
            if(i%prime[j])break;
        }
    }
}

约数求解

试除法求约数

1
2
3
4
5
6
7
8
9
10
11
vector<int> v;
for(int i = 1;i <= a/i;i++){
    if(a % i == 0){
        v.push_back(i);
        if(i != a/i)v.push_back(a/i);
    }
}
sort(v.begin(),v.end());
for(auto t:v){
    cout << t << " ";
}

求约数个数

image-20210825221658353

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
 while(n--){
     int a;
     cin >> a;
     for(int i = 2;i <= a/i;i++){
         if(a % i == 0){
        //注意这里是取模判断，素数一定会在质数判断的时候被除完
             while(a % i == 0){
                 m[i]++;
                 a/=i;
             }
         }
     }
     //注意这里
     if(a > 1)m[a]++;
 }
for(auto a:m){
    //注意这里是对每个乘数取模，这样才能存到longlong里，其中需要对res*j取模，
    //res *= (a.second + 1) % N;  这样写等于没取模
    res = (res*(a.second+1)) % N;
}
cout << res;

约数和：秦九韶算法

image-20210825223455741

最大公约数：辗转相除法

1
2
3
int gcd(int a,int b){
    return b==0?a:gcd(b,a%b);
}

欧拉函数

image-20210825230159042 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
while(n--){
    int a;
    cin >> a;
    //注意这里使用long long,防止越界
    long long r = a;
    for(int i = 2;i <= a/i;i++){
        if(a % i == 0){
            r = r*(i-1)/i;
            while(a % i == 0) a/=i;
        } 
    }
    if(a > 1)r = r*(a-1)/a;
    cout << r << endl;
}

筛法求欧拉和

image-20210826115712665

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void ruler(int n){
    // 首先背线筛的板子
    for(int i = 2;i <= n;i++){
        if(!st[i]){
            p[cnt++] = i;
            //如果是质数,则1~i-1都是互质的数
            phi[i] = i-1;
            st[i] = 1;
        }
        for(int j = 0;p[j] <= n/i;j++){
            st[p[j]*i] = 1;
            //分情况讨论,这里处理的是p[j]*i的欧拉函数
            //如果是i%p[j] == 0,则p[j]*i和i的质因子相同,只需补N值
            if(i % p[j] == 0){
                phi[p[j]*i] = phi[i]*p[j]; 
                break;
            }
            //如果是i%p[j] != 0,则需要在补p[j]的基础上再乘以(p[j]-1/p[j])
            else phi[p[j]*i] = phi[i]*(p[j]-1);
        }
    }
    for(int i = 2;i <= n;i++) r+=phi[i];
}

快速幂

板子

快速幂需要注意%p的位置

1
2
3
4
5
6
7
8
9
10
11
12
13
typedef long long LL;
int qmi(LL a,int b,int p){
    LL r = 1;
    while(b){
        //如果b的二进制表示的第0位为1,则乘上当前的a
        if(b&1) r = (LL)((r*a)%p);
        //右移一位
        b >>= 1;
        //更新a,a依次为a^{2^0},a^{2^1},a^{2^2},....,a^{2^logb}
        a = a*a%p;
    }
    return r;
}

快速幂求逆元

image-20210826131138176

image-20210826131645258

1
2
3
4
5
6
//a = a * b * b^-1 mod p
//∴ b *b^-1mod p==1
//而由小费马定理得 b^p-1 mod p == 1;
//b^-1 == b^p-2;
//即求b^p-2 mod p的值，一个快速幂可以解决
else cout << qmi(a,p-2,p) << endl;

扩展欧几里得算法

image-20210826133840327

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//扩展欧几里得算法在求得gcd的基础上还可以求得一组x,y解
//注意这里必须使用地址符
int exgcd(int a,int b,int &x,int &y){
    if(!b){
        x=1;y=0;
        return a;
    }
    int d = exgcd(b,a%b,y,x);
    /*
        ax + by = by+(a%b)x = d;
        ∴ax+by = by+(a-(a/b)*b)x
        ax+by = by+ax-(a/b)*bx
        ax+by = b(y-(a/b)x)+ax;
        ∴x不变,y=y-(a/b)*x;
    */
    y = y - (a/b)*x;
}

求线性同余方程

image-20210826143242611

1
2
3
4
5
6
7
8
9
10
11
12
int a,b,m,x,y;
cin >> a >> b >> m;
//ax 同余 b mod m的对应条件是存在一组x,y使得ax = my+b
//转一下得ax+my' = b，只要b是gcd(a,m)的倍数，就一定存在一组x,y'=-y使其成立
int d = exgcd(a,m,x,y);
if(b % d != 0) cout << "impossible" << endl;
//题目说答案是int，所以我们%d输出，但是在mod m之前的乘法运算中，就可能暴int了，所以我们这里拿ll接一下

//这里真的是把人差点卡死在这儿
//因为x的结果是ax+my==d的解，不是等于b的解，所以首先要x *(b/d)将数放回去,因为这里可能爆栈所以拿LL先接一下，方便计算
//然后保险起见，用m mod一下即可，根据(a*x) % m = (a * (x % m)) % m，所以保险起见输出为x % m
else cout << (LL)x *(b/d) % m << endl;

中国剩余定理

表达整数的奇怪方式

image-20210829182612966image-20210829182619920

image-20210829182632294

image-20210829182641612

image-20210829182647238

推导过程：

image-20210829184136757

组合数问题

第一种解法：公式法递推

运用公式：Cb/a = Cb/a-1+Cb-1/a-1;

首先将所有的组合数情况用类似DP的方法给计算出来，然后直接哈希对应

1
2
3
4
5
6
7
8
9
10
void init(){
    //从0开始
    for(int i = 0;i <= 2000;i++){
        for(int j = 0;j <= i;j++){
            //j==0时的情况只有什么都不选这一种情况
            if(!j) f[i][j] = 1;
            else f[i][j] = (f[i-1][j-1]+f[i-1][j])%mod;
        }
    }
}

第二种解法：初始化阶乘值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//快速幂的板子
int qmi(int a,int k,int q){
    int res = 1;
    while(k){
        //注意LL
        if(k&1) res = (LL)res*a%q;
        a = (LL)a*a%q;
        k >>= 1;
    }
    return res;
}
int main(){
    int n;
    cin >> n;
    //初始化
    f[0] = inf[0 ] =1;
    for(int i = 1;i < N;i++){
        //注意LL的问题
        f[i] = (LL)f[i-1]*i% mod;
        //在这里使用到了逆元值，inf[i]代表i % mod的逆元，i %mod的逆元为i^m-2;
        inf[i] = (LL)inf[i-1]*qmi(i,mod-2,mod) % mod;
    }
    while(n--){
        int a,b;
        cin >> a >> b;
        //注意LL的问题以及连乘时的两次mod
        cout << (LL)f[a] * inf[a-b]%mod * inf[b]%mod << endl;
    }
    return 0;
}

image-20210829225806186

第三种解法：卢卡斯定理

image-20210829234753028

如何应用：直接应用公式

首先：注意LL

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<iostream>
using namespace std;
typedef long long LL;
int p;
//快速幂
LL qmi(int a,int k,int p){
    LL res = 1;
    while(k){
        if(k&1) res = (LL)res*a%p;
        a = (LL)a*a%p;
        k >>= 1;
    }
    return res;
}
//正常求C的值
LL C(LL a,LL b){
    LL res = 1;
    //上边从a开始，下边从1开始
    for(int i = 1,j = a;i <= b;i++,j--){
        res = (LL)res * j;
        //注意这里：逆元的成立条件中有一个%p，需要确定好p的取值
        res = (LL)res * qmi(i,p-2,p) % p;
    }
    return res;
}
//卢卡斯定理
LL lucas(LL a,LL b){
    //特例判断
    if(a < p && b < p)return C(a,b);
    //否则使用lucas定理开始降维
    //注意公式的适用条件中有一个同余
    else return (LL)C(a%p,b%p) * lucas(a/p,b/p) % p;
}
int main(){
    int n;
    cin >> n;
    while(n--){
        LL a,b;
        cin >> a >> b >> p;
        cout << lucas(a,b) << endl;
    }
    return 0;
}

第四种解法：高精度乘法+质数分解抵消

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include<iostream>
#include<vector>
using namespace std;
const int N = 5010;
int prime[N],cnt;
int sum[N],st[N];
//线性筛法求质数
void get_prime(int a){
    for(int i = 2;i <= a;i++){
        if(!st[i])prime[cnt++] = i;
        for(int j = 0;prime[j] <= a/i;j++){
            st[prime[j]*i] = true;
            if(i % prime[j]==0)break;
        }
    }
}
//得到a!中的p质因子的个数
int get(int a,int p){
    int res = 0;
    while(a){
        res+=a/p;
        a/=p;
    }
    return res;
}
//高精度乘法
vector<int> mul(vector<int> a,int b){
    int t = 0;
    vector<int> res;
    for(int i = 0;i < a.size();i++){
        t += a[i]*b;
        res.push_back(t%10);
        t/=10;
    }
    while(t){
        res.push_back(t%10);
        t/=10;
    }
    // if(t) res.push_back(t);
    while(res.size() && res.back()==0) res.pop_back();
    return res;
}

int main(){
    int a,b;
    cin >> a >> b;
    //对最大值求质数
    get_prime(a);
    //对所有质数求结果中应该有的数量,其中大部分质数的个数都被抵消掉，这里是本算法的核心优化
    for(int i = 0;i < cnt;i++){
        sum[i] = get(a,prime[i])-get(a-b,prime[i])-get(b,prime[i]);
    }
    vector<int> ans;
    //初始化
    ans.push_back(1);
    //对所有质数求结果
    //迭代所有质数
    for(int i = 0;i < cnt;i++){
        //迭代所有个数
        for(int j = 0;j < sum[i];j++){
            ans = mul(ans,prime[i]);
        }
    }
    //输出
    for(int i = ans.size()-1;i >= 0;i--){
        cout << ans[i];
    }
    return 0;
}

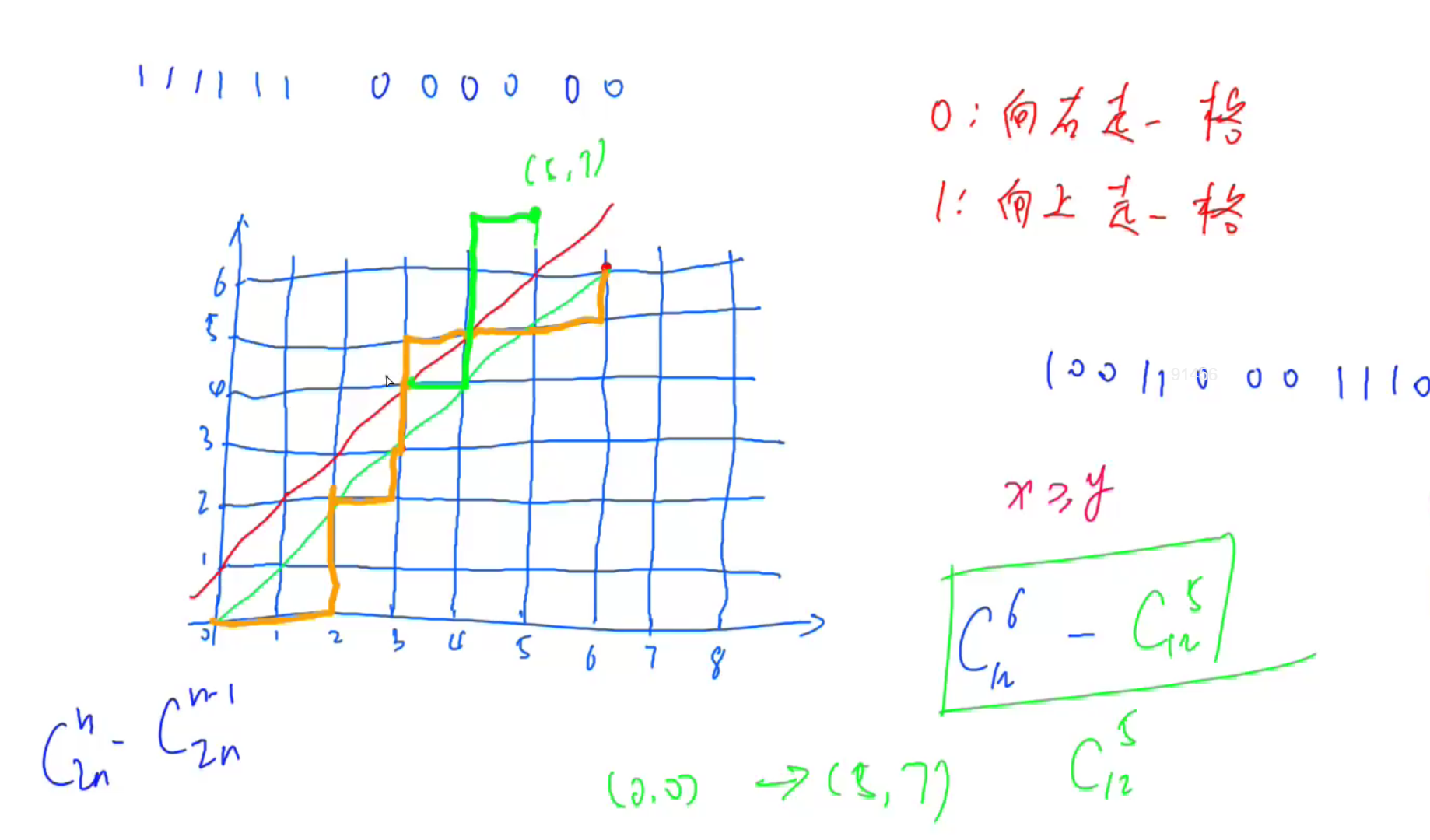
满足条件的01序列

image-20210831151233385

image-20210831151327608

红色线是高压红线。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
//注意这里开大！！！
const int N = 200010,mod = 1e9+7;
LL f[N],inf[N];
LL qmi(int a,int k,int q){
    int res = 1;
    while(k){
        if(k&1) res = (LL)res*a%q;
        a = (LL)a*a%q;
        k >>= 1;
    }
    return res;
}
void init(){
    f[0] = inf[0] = 1;
    for(int i = 1;i < N; i++){
        f[i] = (LL)f[i-1]*i%mod;
        inf[i] = (LL)inf[i-1]*qmi(i,mod-2,mod)%mod;
    }
}
int main(){
    int n;cin >> n;init();
    int res = (LL)f[2 * n]*inf[n] % mod * inf[n] % mod * qmi(n + 1, mod - 2,mod) % mod;
        cout << res << endl;
    return 0;
}

容斥原理

image-20210831202929031

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
//用位运算表示选那几个数字，如果是奇数个则加，如果是偶数个即减。
#include<iostream>
using namespace std;
typedef long long LL;
const int N = 1e9+7,M = 20;
int n,m,f[M];
int main(){
    cin >> n >> m;
    for(int i = 0;i < m;i++){
        cin >> f[i];
    }
    int res=0;
    //位运算迭代
    //枚举从1 到 1111...(m个1)的每一个集合状态, (至少选中一个集合)
    //从1开始枚举， 枚举到 2^m-1
    //一共有2^m-1项（除了一个都不选之外
    for(int i = 1;i < 1 << m;i++){
        //质数乘积
        LL t = 1;
        //位的数量
        int s = 0;
        for(int j = 0;j < m;j++){
            if(i>>j&1){
				//乘积大于n, 则n/t = 0, 跳出这轮循环，可加可不加
                //当前质数的乘积就已经>n了， 直接跳出即可 
                //注意这里需要放到LL
                if((LL)t*f[j] > n){
                    t = -1;break;
                }
                s++;t*= f[j];
            }
        }
        //1~n中能被p整除的个数：n/p下取整
        if(t != -1){
            if(s%2==1) res += n/t;
            else res -= n/t; 
        }
    }
    cout << res;
    return 0;
}

博弈论

公平组合游戏

image-20210831213559881

image-20210831222636790

image-20210831221029922

image-20210831221147080

image-20210831221131911

台阶NIM问题

image-20210831230715516

解：保证奇数点的数量保持一致不变，这样我们一定可以及时走下去

image-20210831230647515

image-20210831230625539 
1
2
3
4
5
6
7
8
9
int cnt = 1;
int res = 0;
while(n--){
    int a;cin >> a;
    if(cnt&1)res ^= a;
    cnt++;
}
if(res) cout << "Yes";
else cout << "No";

集合NIM问题

image-20210831234405143

SG函数：到不了的自然数最小值+1

image-20210901000015149

SG(x) = 0的话，其对应点无法走到终点，因为没有一条数字下降的路。

SG(x) != 0的话，一定能找到一条路，其路可以指向终点SG(0)

多个图的处理：SG(x1)^SG(x2)^…^SG(xn) = 0必败，!=0必胜，其中x1,x2,…,xn是每个图的起点

1.Mex运算:
设S表示一个非负整数集合.定义mex(S)为求出不属于集合S的最小非负整数运算,即:
mes(S)=min{x};
例如:S={0,1,2,4},那么mes(S)=3;

2.SG函数
在有向图游戏中,对于每个节点x,设从x出发共有k条有向边,分别到达节点y1,y2,····yk,定义SG(x)的后记节点y1,y2,····
yk的SG函数值构成的集合在执行mex运算的结果,即:
SG(x)=mex({SG(y1),SG(y2)····SG(yk)})
特别地,整个有向图游戏G的SG函数值被定义为有向图游戏起点s的SG函数值,即 SG(G)=SG(s).

3.有向图游戏的和
设G1，G2,····,Gm是m个有向图游戏.定义有向图游戏G,他的行动规则是任选某个有向图游戏Gi,并在Gi上行动一步.G被称为有向图游戏G1,G2,·····,Gm的和.
有向图游戏的和的SG函数值等于它包含的各个子游戏SG函数的异或和,即:
SG(G)=SG(G1)xorSG(G2)xor···xor SG(Gm)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int sg(int x){
    //记忆化搜索
    if(f[x] != -1)return f[x];
    set<int> S;
    //对所有可能连接到的情况进行迭代，如果x>s[i]，则存入x-s[i]对应的点，加上该分支
    for(int i = 0;i < n;i++){
        if(x>=s[i])S.insert(sg(x-s[i]));
    }
    //判断所有分支的最大值
    for(int i=0;;i++){
        //找到最大值赋值
        if(!S.count(i))return f[x] = i;
    }
}
int sg(int x){
	if(f[x]!=-1)return f[x];
    set<int> S;
    for(int i = 0;i < n;i++){
        if(x>=s[i])S.insert(sg(x-s[i]));
    }
    for(int i = 0;;i++){
        if(!s.count(i))return f[x]=i;
    }
}
int main(){
    cin >> n;
    for(int i = 0;i < n;i++)cin >> s[i];
    cin >> k;
    int res = 0;
    memset(f,-1,sizeof f);
    for(int i = 0;i < k;i++){
        int m;cin >> m;
        res^=sg(m);
    }
    
    if(res) cout << "Yes";
    else cout << "No";
    return 0;
}

拆分NIM游戏

image-20210901135552976

1
2
3
4
5
6
7
8
9
10
11
12
int sg(int x){
    if(f[x]!=-1)return f[x];
    set<int> S;
    for(int i = 0;i < x;i++){
        for(int j = 0;j <= i;j++){
            S.insert(sg(i)^sg(j));
        }
    }
    for(int i = 0;;i++){
        if(!S.count(i)) return f[x] = i;
    }
}

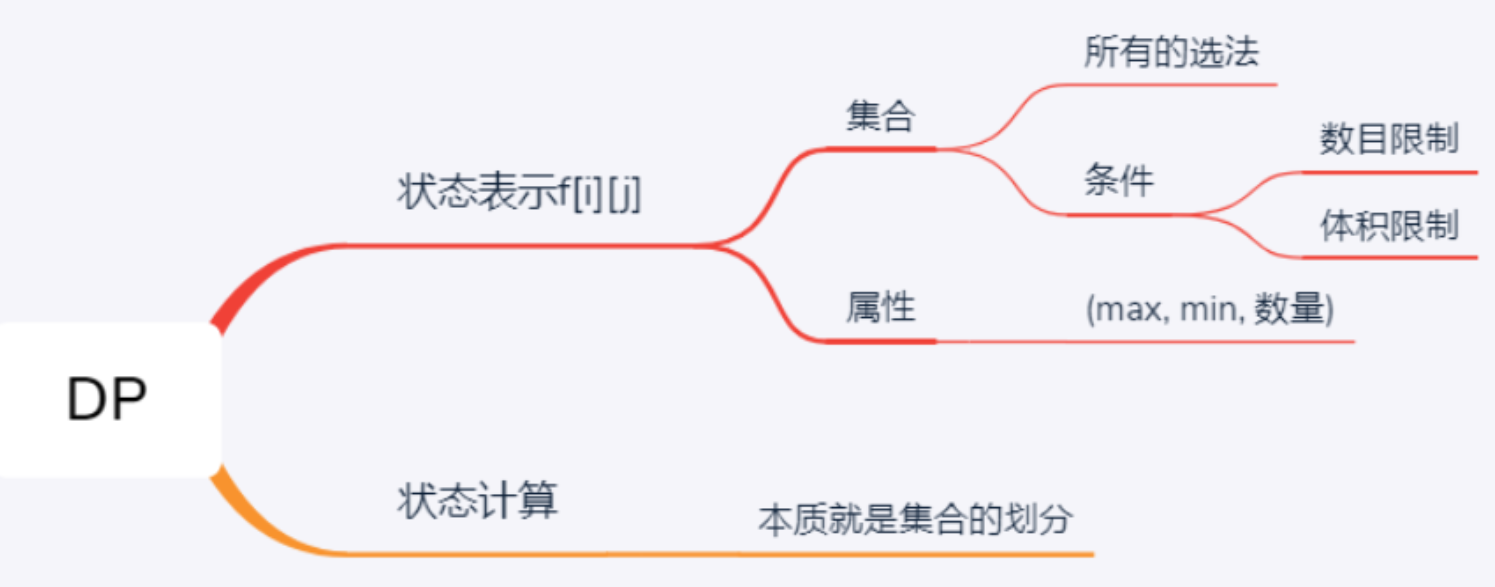
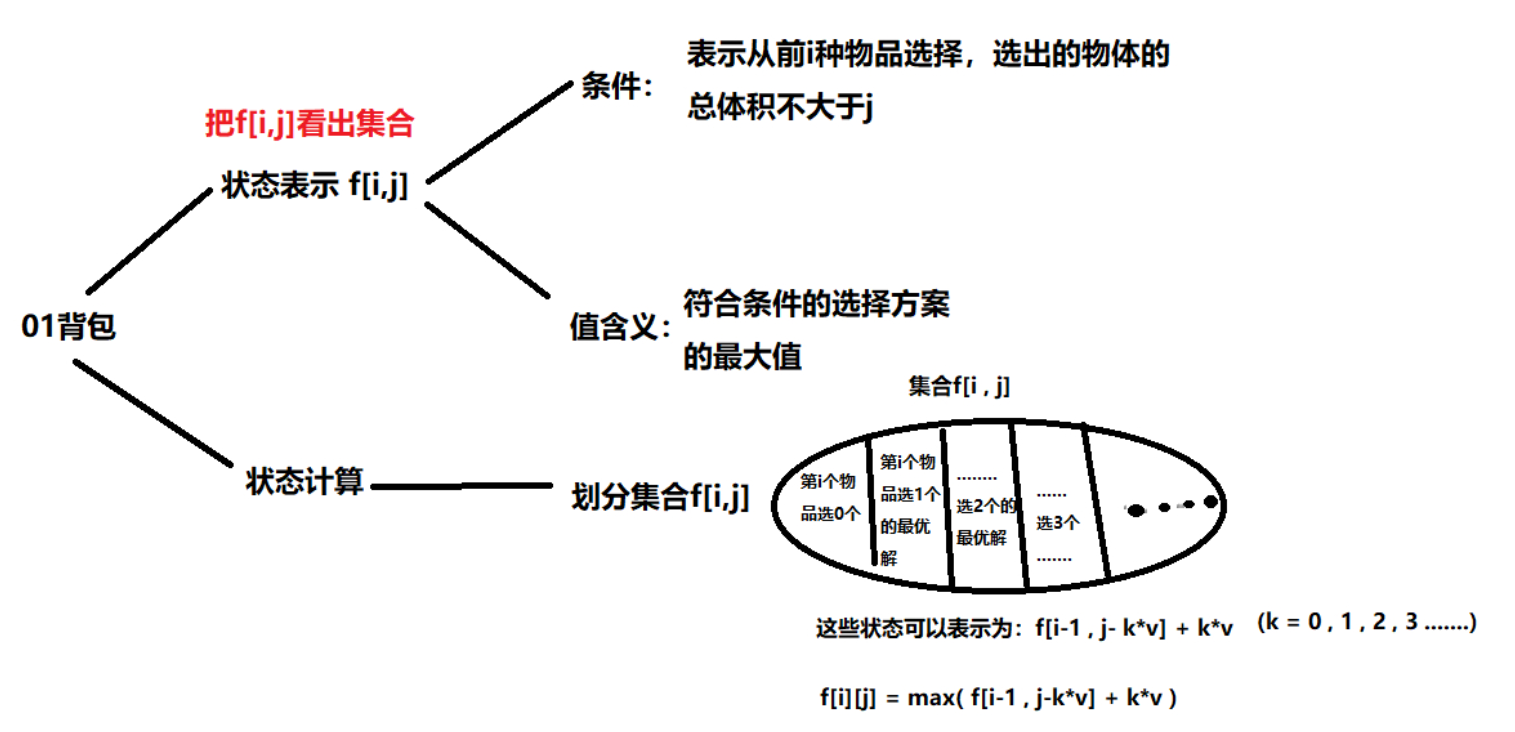
背包问题

image-20210826144543958

01背包：每个物品只有一件

image-20210826144432994

二维解法

1
2
3
4
5
6
7
8
9
10
11
int f[N][N];
int w[N],v[N];
for(int i = 0;i <= n;i++){
    for(int j = 0;j <= m;j++){
        //放物品,如果当前的容量够放得下当前物品
        if(j >= v[i]){
            f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i]);
        }
    }
}
cout << f[n][m] << endl;

一维解法

1
2
3
4
5
6
7
8
9
10
11
12
13
int f[N][N];
int w[N],v[N];
//降到一维之后，原有的不选第i个物品就直接随着i的增加而自动迭代到了下一层
//但是，如果还是从小到大进行迭代，可能f[i][j]需要f[i-1][j-v[i]]的值，但是f[i-1][j-v[i]]在前面迭代成了f[i][j-v[i]]
//所以有数据污染的危险，因此对j需要从大到小处理
for(int i = 1;i <= n;i++){
    //这里直接处理到v[i]，即将原有的if条件等价到这里
    for(int j = m;j >= v[i];j--){
        f[j] = max(f[j],f[j-v[i]]+w[i]);
    }
}
//因为我们一直算的是max值，所以推到m的时候的结果一定是全局最优解
cout << f[m] << endl;

完全背包：不规定物品件数

image-20210826150626209

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/*
    01背包的转移方程 f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i])
    完全背包中选择第i件物品的推导
    f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i],f[i-1][j-2v[i]]+2w[i]+...)
    减一个v
    f[i][j-v[i]] = max(f[i-1][j-v[i]],f[i-1][j-2v[i]]+w[i],f[i-1][j-3v[i]]+2w[i]+...)
    所以
    完全背包转移方程 f[i][j] = max(f[i-1][j],f[i][j-v[i]]+w[i])
    
    所以01背包和完全背包的区别在于选择i时的更新是从i-1更新还是从i更新
    
    所以01背包从后往前遍历，防止i-1 --> i
    而完全背包正需要将i-1 --> i，所以从前向后遍历
    
*/
for(int i = 1;i <= n;i++){
    //从v[i]开始
    for(int j = v[i];j <= m;j++){
        f[j] = max(f[j],f[j-v[i]]+w[i]);
    }
}

两个代码其实只有一句不同（注意下标）

f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);//01背包

f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);//完全背包问题

多重背包：规定每个物品的件数

image-20210826150820966

在01背包的基础上加入一套循环，每次加入k件物品，进行判断（O(N3))

1
2
3
4
5
6
7
8
9
10
for(int i = 1;i <= n;i++){
    int v,w,s;
    cin >> v >> w >> s;
    //注意这里需要从大到小进行处理
    for(int j = m;j >= v;j--){
        for(int k = 1;k <= s;k++){
            if(j >= k*v) f[j] = max(f[j],f[j-k*v]+k*w);
        }
    }
}

优化：使用快速幂的思路，重新创造一个物品列表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
struct Good{
    int v,w;
};

int main(){
    int n,m;
    cin >> n >> m;
    vector<Good> g;
    for(int i = 1;i <= n;i++){
        int v,w,s;
        cin >> v >> w >> s;
        //注意每次对g进行清理
        g.clear();
        //重新创建一个序列，按照二进制的规则存储
        for(int j = 1;s >= j;j*=2){
            g.push_back({j*v,j*w});
            s-=j;
        }
        //如果s有剩余，也存进去，防止漏掉物品
        if(s)g.push_back({s*v,s*w});
        //对当前的新物品列表进行01背包
        for(auto a:g){
            for(int j = m;j >= a.v;j--){
                f[j] = max(f[j],f[j-a.v]+a.w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

分组背包：每个组内01背包

image-20210826160014477

1
2
3
4
5
6
7
8
9
10
11
for(int i=1;i<=n;i++){
    cin>>s[i];
    for(int j=0;j<s[i];j++)
        cin>>v[i][j]>>w[i][j];
}
for(int i=1;i<=n;i++){
    for(int j=m;j>=0;j--){
        for(int k=0;k<s[i];k++)
            if(v[i][k]<=j) f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
    }
}

线性DP问题

线性DP问题一般都涉及到位置计算。

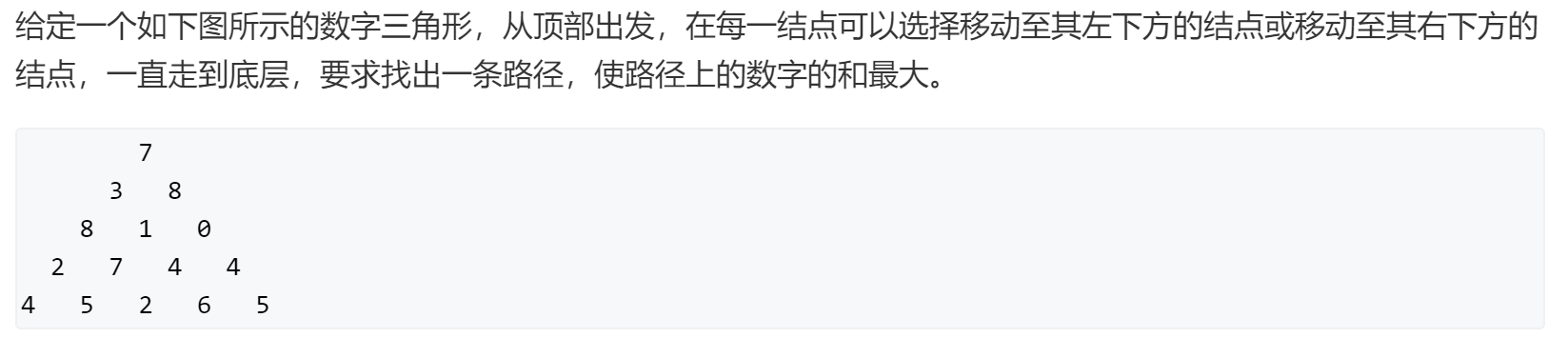
数字三角形

image-20210826165855069

1
2
3
4
5
6
//从下向上可以解决分支问题
for(int i = n-1;i > 0;i--){
    for(int j = 1;j <= i;j++){
        f[i][j] = max(f[i+1][j],f[i+1][j+1])+f[i][j];
    }
}

最长上升子序列：使用二分进行优化

image-20210826172152769

原理：

题解中最难理解的地方在于栈中序列虽然递增，但是每个元素在原串中对应的位置其实可能是乱的，那为什么这个栈还能用于计算最长子序列长度？
实际上这个栈【不用于记录最终的最长子序列】，而是【以stk[i]结尾的子串长度最长为i】或者说【长度为i的递增子串中，末尾元素最小的是stk[i]】。理解了这个问题以后就知道为什么新进来的元素要不就在末尾增加，要不就替代第一个大于等于它元素的位置。
这里的【替换】就蕴含了一个贪心的思想，对于同样长度的子串，我当然希望它的末端越小越好，这样以后我也有更多机会拓展。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include<iostream>
using namespace std;
const int N = 100010;
int f[N],n;
int g[N];
int main(){
    cin >> n;
    for(int i = 1;i <= n;i++)cin >> f[i];
    //替换思想体现了贪心，我们希望序列每个位置的数都更小
    g[1] = f[1];
    int t = 1;
    for(int i = 2;i <= n;i++){
        //如果当前序列的最大值小于f[n]，则加入数组
        if(g[t] < f[i]){
            g[t+1] = f[i];
            t++;
        }
        else {
            //找到第一个大于等于f[n]的值
            int l = 1,r = t;
            while(l < r){
                int m = (l+r)/2;
                if(g[m] >= f[i]) r = m;
                else l = m+1;
            }
            g[l] = f[i];
        }
    }
    cout << t << endl;
    return 0;
}

最长公共子序列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*
    分析
    状态表示 f[i][j]
            定义：表示a的前i个字符和b的前j个字符所组成的所有子序列
            属性：长度最大值
    状态计算：看成集合
            这个状态下产生不同的原因是是否有a[i]或者b[j]
            f[i][j]的计算针对于a[i],b[j]可以由以下几个部分组成：
                1、有a[i]和b[j]     if(a[i] == b[j]) f[i][j] = f[i-1][j-1]+1;
                2、没有a[i]或b[j]    f[i][j] = f[i-1][j-1]
                3、有a[i]没b[j]   f[i][j-1]表示的是a的前i个字符和b的前j-1个字符的子序列最大值，虽然不一定包含b[j],但包含了当前情况。而且f[i][j-1]是不超过集合f[i][j]的，即f[i][j-1]集合的最大值包含当前情况且没有出界。所以可以用f[i][j-1]代替本情况
                4、有b[i]没a[i]   同上,用f[i-1][j]代替本情况
                
*/ 
for(int i = 1;i <= n;i++){
    for(int j = 1;j <= m;j++){
        //分情况讨论
        if(a[i]==b[j]) f[i][j] = f[i-1][j-1]+1;
        else{
            f[i][j] = max(f[i-1][j],f[i][j-1]);
        }
    }
}
cout << f[n][m] << endl;

最短编辑距离

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*
    1、状态表示：f[i][j]
        定义：从a[1..i]到b[1..j]的操作
        属性：求操作次数最小值
    2、状态计算：（从最后的操作出发）
        对于一个f[i][j]，求解的情况有三种（注意这里，对a的删除理论上和对b的增加一致，所以只考虑对a的操作）
        a.删除   f[i][j] = f[i-1][j]+1 （从a的后面删除一个字符）
        b.增加   f[i][j] = f[i][j-1]+1 （在a的后面增加一个字符）
            最后一步是增加：若最后一步是增加，为了使a[1 ~ i] = b[1 ~ j]那最后一步增加的一定是b[j]。
            那么f[i][j]就可以看成是，首先将a[1 ~ i]转化成b[1 ~ j - 1]，这时候所操作的步骤数为f[i][j - 1]，下一步在b[j - 1]后面添加一个b[j]，那么f[i][j] = f[i][j - 1] + 1。
            也就是说，我们的转化过程为：a[1 ~ i] -> b[1 ~ j - 1] -> b[1 ~ j]，
            f[i][j]的意义是将a[1 ~ i]转化为b[1 ~ j]的步骤数，不能理解为直接在a[i]后面添加一个数，这是一个动态的变化的过程。
        c.修改   f[i][j] = if(a[i] == b[j])f[i-1][j-1]（不用改） else f[i-1][j-1]+1（加上修改操作）
*/

//边界条件
//判断一下是否需要边界条件
//只进行增加操作
for(int i = 0;i <= m;i++)f[0][i] = i;
//只进行删除操作
for(int i = 0;i <= n;i++)f[i][0] = i;

for(int i = 1;i <= n;i++){
    for(int j = 1;j <= m;j++){
        //四种情况
        //增加与删除
        f[i][j] = min(f[i-1][j]+1,f[i][j-1]+1);
        //不动与替换
        f[i][j] = min(f[i][j],f[i-1][j-1]+(a[i]!=b[j]));
    }
}
cout << f[n][m];

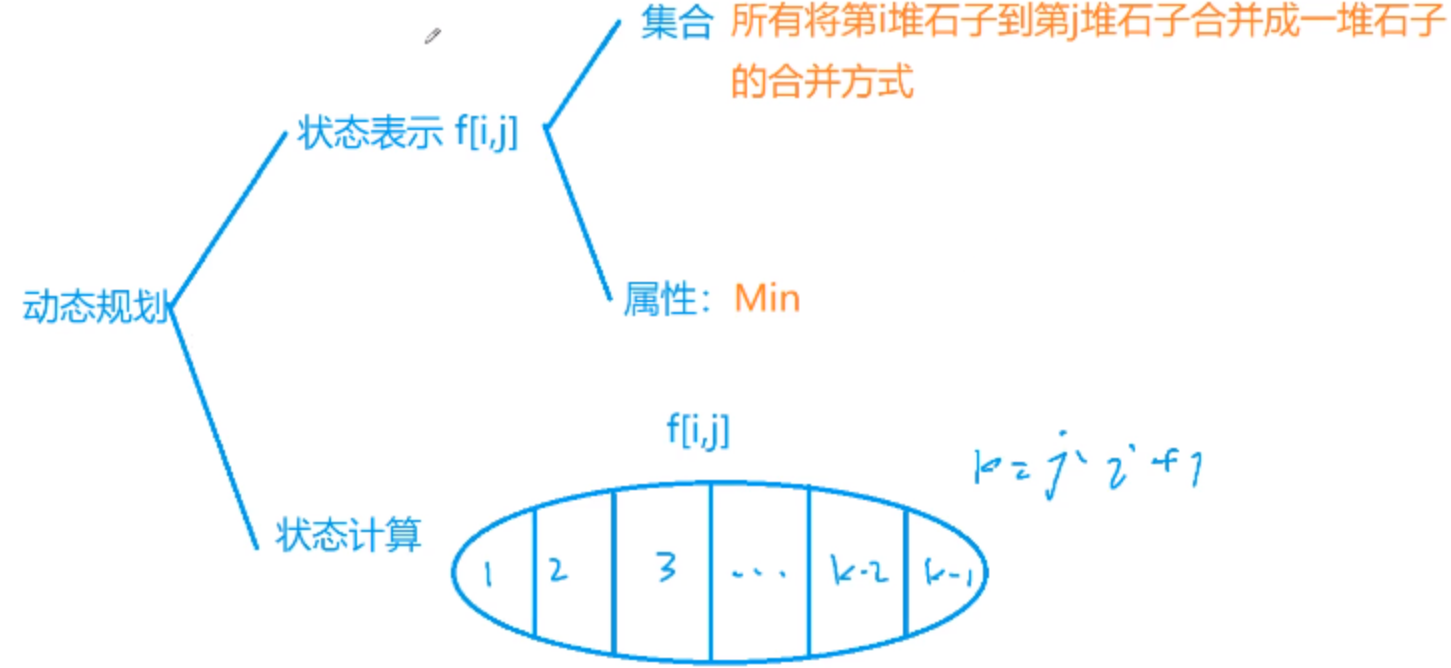
区间DP

石子合并

image-20210827130138656

image-20210827121556326

image-20210827123510128

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<iostream>
#include<cstring>
using namespace std;
const int N = 310;
/*
    1、集合表示f[i][j]
        定义：从第i个石子到第j个石子的所有合并情况
        属性：代价最小值
    2、集合计算
        对于一个从i到j的集合，可以从[i,i],[i+1,j] / [i,i+1],[i+2,j] / ... / [i,k],[k+1,j] / ... / [i,j-1],[j,j]这样来枚举
        即对每一个可能的合并情况进行处理
*/

int n;
int s[N],a[N],f[N][N];
int main(){
    cin >> n;
    for(int i = 1;i <= n;i++)cin >> a[i];
    for(int i = 1;i <= n;i++)s[i] = a[i]+s[i-1];

    //长度为1时不需要合并，为0
    // for(int i = 1;i <= n;i++)f[i][i] = a[i];
    //区间dp的第一步一般为对区间长度进行枚举
    //O(n^3)的时间复杂度
    for(int len = 2;len <= n;len++){		//区间枚举
        for(int i = 1;i + len-1 <= n;i++){	//起点迭代
            int j = i+len-1;				//计算终点
            f[i][j] = 1e7;
            //转移方程						
            for(int k = i;k <= j-1;k++){	//状态转移
                f[i][j] = min(f[i][j],f[i][k]+f[k+1][j]);
            }
            f[i][j] += s[j]-s[i-1];
        }
    }
    cout << f[1][n];
    return 0;
}

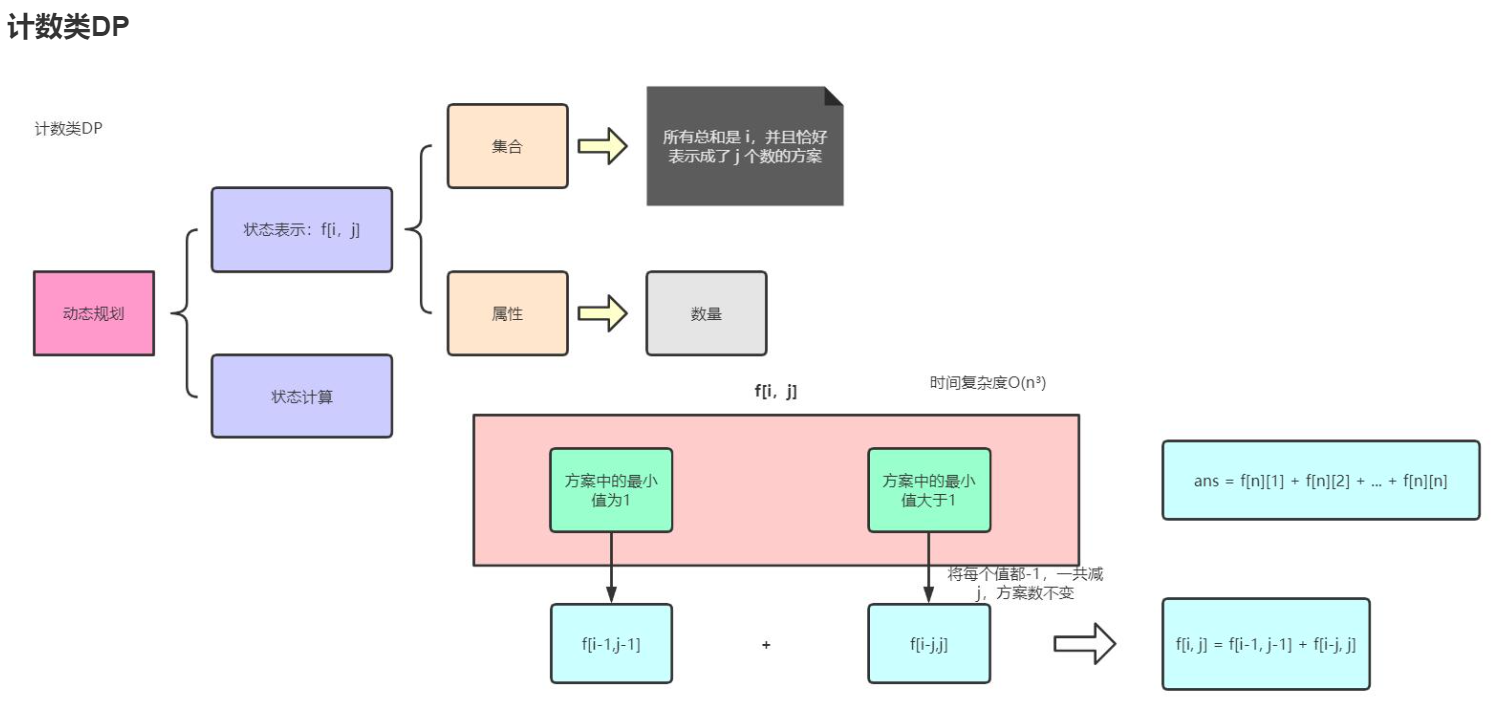
计数DP

image-20210827130855450

image-20210827150150578

image-20210827150207137

数位统计DP

计数问题

状态压缩DP

蒙特卡罗的梦想

image-20210827151843247

image-20210827164455255

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<bits/stdc++.h>
using namespace std;
const int N=12, M = 1<< N;  
long long f[N][M] ;// 第一维表示列， 第二维表示所有可能的状态
bool st[M];  //存储每种状态是否有奇数个连续的0，如果奇数个0是无效状态，如果是偶数个零置为true。
//vector<int > state[M];  //二维数组记录合法的状态
vector<vector<int>> state(M);  //两种写法等价:二维数组
int m , n;

int main(){

    while(cin>>n>>m, n||m){ //读入n和m，并且不是两个0即合法输入就继续读入
        //第一部分：预处理1
        //对于每种状态，先预处理每列不能有奇数个连续的0
        for(int i=0; i< 1<<n; i++){
            int cnt =0 ;//记录连续的0的个数
            bool isValid = true; // 某种状态没有奇数个连续的0则标记为true
            for(int j=0;j<n;j++){ //遍历这一列，从上到下
                 if( i>>j &1){  //i>>j位运算，表示i（i在此处是一种状态）的二进制数的第j位； &1为判断该位是否为1，如果为1进入if
                    if(cnt &1) { //这一位为1，看前面连续的0的个数，如果是奇数（cnt &1为真）则该状态不合法
                        isValid =false;break;
                    } 
                    cnt=0; // 既然该位是1，并且前面不是奇数个0（经过上面的if判断），计数器清零。//其实清不清零没有影响
                 }
                 else cnt++; //否则的话该位还是0，则统计连续0的计数器++。
            }
            if(cnt &1)  isValid =false; //最下面的那一段判断一下连续的0的个数
            st[i]  = isValid; //状态i是否有奇数个连续的0的情况,输入到数组st中
        }

        //第二部分：预处理2
        // 经过上面每种状态 连续0的判断，已经筛掉一些状态。
        //下面来看进一步的判断：看第i-2列伸出来的和第i-1列伸出去的是否冲突

        for(int j=0;j< 1<<n;j++){ //对于第i列的所有状态
            state[j].clear(); //清空上次操作遗留的状态，防止影响本次状态。
            for(int k=0;k< 1<<n;k++){ //对于第i-1列所有状态
                if((j&k )==0 && st[ j| k] ) // 第i-2列伸出来的 和第i-1列伸出来的不冲突(不在同一行) 
                //解释一下st[j | k] 
                //已经知道st[]数组表示的是这一列没有连续奇数个0的情况，
                //我们要考虑的是第i-1列（第i-1列是这里的主体）中从第i-2列横插过来的，还要考虑自己这一列（i-1列）横插到第i列的
                //比如 第i-2列插过来的是k=10101，第i-1列插出去到第i列的是 j =01000，
                //那么合在第i-1列，到底有多少个1呢？自然想到的就是这两个操作共同的结果：两个状态或。 j | k = 01000 | 10101 = 11101
                //这个 j|k 就是当前 第i-1列的到底有几个1，即哪几行是横着放格子的
                    state[j].push_back(k);  //二维数组state[j]表示第j行， 
                    //j表示 第i列“真正”可行的状态，如果第i-1列的状态k和j不冲突则压入state数组中的第j行。
                    //“真正”可行是指：既没有前后两列伸进伸出的冲突；又没有连续奇数个0。
            }

        }

        //第三部分：dp开始
        memset(f,0,sizeof f);  //全部初始化为0，因为是连续读入，这里是一个清空操作。类似上面的state[j].clear()
        f[0][0]=1 ;// 这里需要回忆状态表示的定义，按定义这里是：前第-1列都摆好，且从-1列到第0列伸出来的状态为0的方案数。
        //首先，这里没有-1列，最少也是0列。其次，没有伸出来，即没有横着摆的。即这里第0列只有竖着摆这1种状态。
        for(int i=1;i<= m;i++){ //遍历每一列:第i列合法范围是(0~m-1列)
            for(int j=0; j< 1<<n; j++){  //遍历当前列（第i列）所有状态j
                for( auto k : state[j])    // 遍历第i-1列的状态k，如果“真正”可行，就转移
                    f[i][j] += f[i-1][k];    // 当前列的方案数就等于之前的第i-1列所有状态k的累加。
            }
        }
        //最后答案是什么呢？
        //f[m][0]表示 前m-1列都处理完，并且第m-1列没有伸出来的所有方案数。
        //即整个棋盘处理完的方案数
        cout<< f[m][0]<<endl;

    }
}

最短哈密顿路径（旅行商问题）

image-20210828111300203

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/*
    分析：
    状态表示：f[i][j]
        定义：在完成i的状态路径之后（i表示走过的点）到达j点的所有路径集合
        计算：权重最小值
    状态计算：
        因为到了j点，所以j点是确定的，不确定的是从哪个点到达的k点
        所以转移方程是
        f[state][j] =  min(f[state][j],f[state ^ 1<<j][k] + w[k][j])
        即我们只需要注意走过哪些点、走到哪个点，共两种情况
        因为如果走的是相同的点，所形成的所有路径中一定有一个最小值，而且其他路径都可以用其代替
        注意：初始化是从第0个点开始，state用二进制表示当前所在的点，所以f[1][0]=0;代表从0开始
*/


image-20210828104558147

image-20210915004217354

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//DP
//初始化每个点都没有连
memset(g,0x3f,sizeof g);
//从1点开始
g[1][0] = 0;

//确定当前状态，即哪些点被用过
for(int i = 0;i < 1<<n;i++){
    //当前停在了哪个点上
    for(int j = 0;j < n;j++){			//确定了所用点和所停点，即可确定序列
        //如果当前状态包含j，即j有效
        if(i>>j & 1){
            //j确定，迭代之前一个的k状态，判断更新最小距离
            for(int k = 0;k < n;k++){
                //如果k状态也包含
                if(i>>k & 1){
                    //更新最小值g[i-(1<<j)][k]，将j去除之后的k结果
                    g[i][j] = min(g[i][j],g[i-(1<<j)][k]+f[k][j]);
                }
            }
        }
    }
}
//输出
cout << g[(1<<n)-1][n-1];

树形DP

没有上司的酒会

image-20210828111946980

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
void dfs(int n){
    //如果选择n点，加上happy值
    f[n][1] = happy[n];
    //对其上司进行处理
    for(int i = h[n];i != -1;i = ne[i]){
        int down = e[i];
        dfs(down);
        //如果不选n点，down可能选可能不选
        f[n][0] += max(f[down][1],f[down][0]);
        //如果选n点，down点一定不会被选
        f[n][1] += f[down][0];
    }
}

int main(){
    cin >> n;
    memset(h,-1,sizeof h);
    for(int i = 1;i <= n;i++)cin >> happy[i];
    //建树
    for(int i = 0;i < n-1;i++){
        int a,b;
        cin >> a >> b;
        add(b,a);
        upper[a] = 1;
    }
    //找根节点
    int root = 1;
    while(upper[root])root++;
    //从根节点进行迭代
    dfs(root);
    cout << max(f[root][0],f[root][1]) << endl;
    return 0;
}

记忆化搜索

记忆化搜索一般跟着dfs一起使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int dp(int x,int y){
    if(f[x][y]) return f[x][y];//如果已经记录过了，就不用再算了 
    f[x][y]=1;
    for(int i=0;i<4;i++)
    {
        int xx=x+dx[i];//到下一个点 
        int yy=y+dy[i];
        if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&h[x][y]>h[xx][yy])//点在范围内，且此点高度，比刚才的点矮就滑过去 
        {
            f[x][y]=max(f[x][y],dp(xx,yy)+1);//比较大小，取出最大的 
        }                                       //+1，是因为如果到从两个点的滑雪距离一样的话，再滑一步，就滑到x，y这个点了，所以+1 
    }
    return f[x][y];//返回最终值 
}

划分数

image-20210914152204058

image-20210914152628226

image-20210914152609245

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int N = 12;
LL f[N][N];
int main(){
    LL a,b;
    while(cin >> a >> b){
//         cout << a << " " << b <<endl;
        memset(f,0,sizeof f);
        for (int i = 1; i <= a; ++i)
            f[i][0] = 0;
        for (int j = 1; j <= b; ++j)
            f[0][j] = 1;
        for(int i = 1;i <= a;i++){
            for(int j = 1; j <= b;j++){
                if(i >= j)f[i][j] = f[i][j-1]+f[i-j][j];
                else f[i][j] = f[i][i];
            }
        }
        cout << f[a][b] <<endl;
    }
    return 0;
}

区间问题

区间选点（最大不相交区间数）

image-20210828221114654

右端点排序。每次优先找最右端点，如果当前最右点小于下一个区间的最左点，则前面所有区间的最右边和下一区间的最左边没有相交，即多一个新的区间。·

image-20210828220535066

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 for(int i = 0;i < n;i++){
        int l,r;
        cin >> l >> r;
        e[i]={l,r};
    }
//按右端点排序
    sort(e,e+n,cmp);
    int r = -2e9;
    int sum = 0;
//更新端点
    for(int i = 0;i < n;i++){
        int tl = e[i].l;
        if(r<tl){
            sum++;
            r = e[i].r;
        }
    }
    cout << sum << endl;

区间分组（教室安排问题）

左端点排序。找到最靠左的右端点，如果最靠左的max_r < l，代表存在一个组可以放入这个区间。

image-20210829133130091

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
sort(p,p+n,cmp);
//我们的小根堆始终保证所有组中的最小的右端点为根节点
priority_queue<int,vector<int>,greater<int>> q;

for(int i = 0;i < n;i++){
    int l = p[i].l;
    //如果还没有分组，或者当前最小右端点还要大于区间左端点
    if(q.empty() || l <= q.top()){
        //所以需要新开一个分组
        q.push(p[i].r);r++;
    }
    else{
        //否则存在一个组可以放入
        //弹出之前的最小右端点并放入当前的右端点
        q.pop();q.push(p[i].r);
    }
}



//左端点排序
sort(p,p+n,cmp);
pri q;
for(int i = 0;i < n;i++){
    //如果满足条件
    if(q.empty()||p[i].l <= q.top()){
        q.push(p[i].r);
    }
    else{
        q.pop();q.push(p[i].r);
    }
}

区间覆盖

image-20210829135504450

左端点排序，在左端点小于s的情况下优先找右端点最大的区间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
for(int i = 0;i < n;i++){
    //注意初始化
    int j = i,r = -2e9;
    //判断当前的l小于st的每个区间，找到右端最远的区间
    while(j < n && p[j].l <= s){
        //如果小于，则将最右端更新成最远的那个点
        r = max(r,p[j].r);
        j++;
    }
    //首先判断是否有断点
    if(r < s) break;
    //否则当前满足区域，将该区域加到res中
    res++;
    //其次判断是否完成搜索
    if(r >= t){
        sc = true;break;
    }
    //如果没完成，则将s更新，继续遍历
    s = r;
    //注意倒退操作
    i = j-1;
}
if(sc) cout << res;
else cout << -1;

总结

区间选点问题：右排序，优先选择最右点

区间分组问题：左排序，如果最小分组的max_r都大于当前区间的l，则代表区间与所有分组有冲突，新开一组

区间覆盖问题：左排序，如果l<s，则找到其符合条件区间的最右端点并更新成s，注意判断断点和结束点

哈夫曼树

image-20210829160917625

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//小根堆
priority_queue<int,vector<int>,greater<int>> q;
while(n--){
    int t;
    cin >> t;
    q.push(t);
}
int r = 0;
while(q.size()>1){
    int a = q.top();q.pop();
    int b = q.top();q.pop();
    int c = a+b;r+=c;
    q.push(c);
}

排序不等式

image-20210829163822491

image-20210829163918358

绝对值不等式

货仓选址

image-20210829164000459

​ 优先向中间建货仓

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<iostream>
#include<algorithm>
using namespace std;
int n;
const int N = 100010;
int f[N];
int main(){
    cin >> n;
    for(int i = 0;i < n;i++)cin >> f[i];
    sort(f,f+n);
    int r = 0;
    int m = n/2;
    for(int i = 0;i < n;i++){
        r += abs(f[i]-f[m]);
    }
    cout << r;
    return 0;
}

公式推导

image-20210829165354551

日期类

1
2
3
4
5
6
7
8
9
10
int months[2][13] = {
        {0,31,28,31,30,31,30,31,31,30,31,30,31},
        {0,31,29,31,30,31,30,31,31,30,31,30,31},
};
bool isLeap(int y){
    return (y%4==0&&y%100!=0)||y%400==0;
}
int years[2] = {365,366};
string s[10]={"Friday","Saturday","Sunday","Monday","Tuesday","Wednesday","Thursday"};

学习笔记
#机试
机试复习
http://paopao0226.site/post/48f084a8.html
作者
Ywj226
发布于
2022年8月18日
更新于
2023年9月23日
许可协议