循环神经网络笔记
本文最后更新于:几秒前
《神经网络与机器学习》第五章笔记
引言
有限自动机
有限状态机是一种用来进行对象行为建模的工具,其作用主要是描述对象在它的生命周期内所经历的状态序列,以及如何响应来自外界的各种事件。在计算机科学中,有限状态机被广泛用于建模应用行为、硬件电路系统设计、软件工程,编译器、网络协议、和计算与语言的研究。
图灵机
控制器可以存储当前自身的状态;读写头,可以读、写存储带上小方格的数字/字母。在工作过程中,图灵机可以根据读写头读到数字/字母和程序更改自身的状态。
以上的机器中都用到了之前的状态对之后的状态的影响和修改,这要求机器本身需要有记忆能力,即对之前的状态进行保存与修正。循环神经网络,即为在前馈网络等的基础上加入记忆元素的网络。
延时神经网络
建立额外的延时单元保存网络的历史信息(包括输入、输出、隐状态等)。
$$
\pmb h_t ^{(l)} = f(\pmb h_t ^{(l-1)},\pmb h_{t-1} ^{(l-1)},…,\pmb h_{t-K} ^{(l-1)})
$$
其中$K$在不同层数$l$上有所不同。延时单元本身基于前馈神经网络。
自回归模型
一种时间序列模型,使用变量$y$的历史信息来预测当前的$y$,即:
$$
\pmb y_t = w_0 + \sum_{k=1} ^K w_k \pmb y_{t-k} + \epsilon_t
$$
其中,$w_0$是模型偏置,可以理解为$b$;$\epsilon_t$是模型噪声,可以使用高斯噪声$\epsilon _t \sim N(0,\sigma^2)$
有外部输入的非线性模型是在上述模型的基础上进一步引入输入$\pmb x$的影响。
$$
\pmb y_t = f(\pmb x_t ,\pmb x_{t-1},…,\pmb x_{t-K_x},\pmb y_{t-1}, \pmb y_{t-2},…,\pmb y_{t-K_y})
$$
其中$f(·)$表示非线性函数,其可以是一个前馈网络,$K_x$和$K_y$是超参数。
循环神经网络
循环神经网络在借用了自回归的变量存储思路,使用一个带自反馈的神经元来处理任意长度的时序数据,这相对于之前的延时模型和自回归模型有很大的改进。
$$
\pmb h_t = f(\pmb h_{t-1},\pmb x_t)
$$
其中$\pmb h_{t-1}$是对前一个活性值状态的记忆,这种记忆的实现可以采用之前提到的延时器等实现,这种基于输入$x$和前一整体状态$\pmb h$的思想与残差思想有所重合。
循环神经网络比前馈神经网络更加符合生物神经网络的结构,也因此在序列识别任务,如语音、自然语言等任务上有很广泛的应用。
循环神经网络的时间维度上由于按时间扩展,其深度很深;在每个时间刻度的层次维度上只有一个$\pmb h_t$作为非线性处理输入给出输出,因此深度较浅。
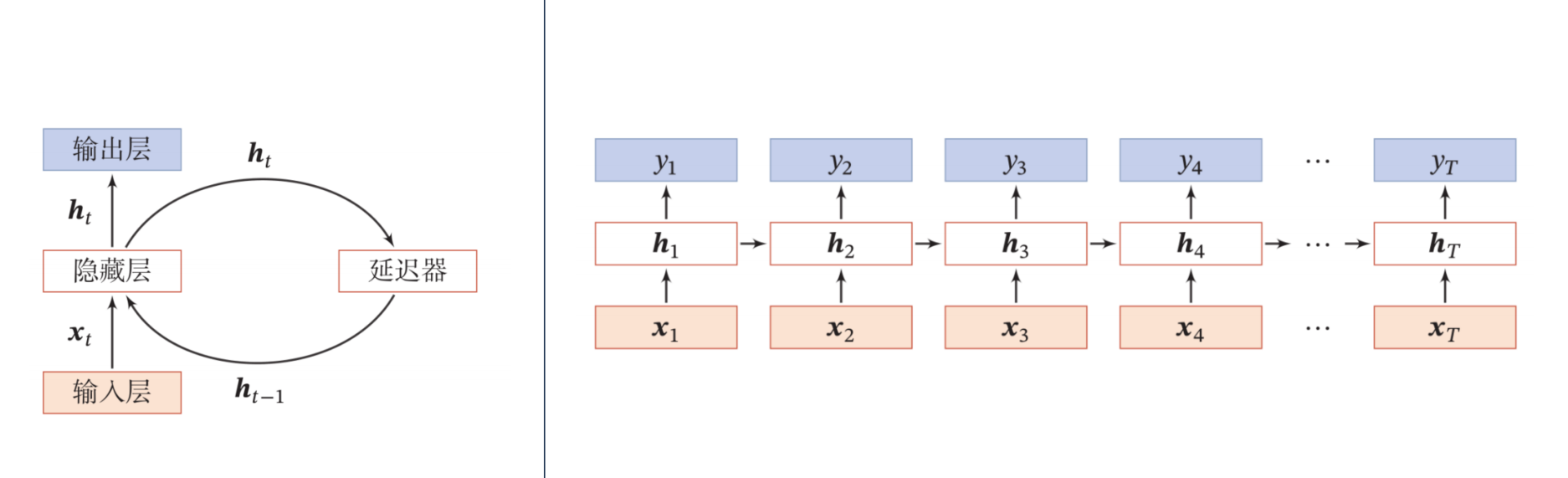
循环网络的相关定理
定理1:循环神经网络的通用近似定理
如果一个完全连接的循环神经网络有足够数量的$sigmoid$型隐藏神经元,它可以以任意的准确率去近似一个任意的非线性动力系统。
$$
\begin{align}
\pmb s_t & = g(\pmb s_{t-1}, \pmb x_t) \\\
\pmb y_t & = o(\pmb s_t)
\end{align}
$$
其中$\pmb s_t$是每个时刻的隐状态,$\pmb x_t$是外部输入,$g(·)$是可测的状态转换函数,$o(·)$是连续输出函数,且对状态空间的紧致性没有限制。
这个定理告诉我们,一个完全连接的循环神经网络可以近似任意一个可行程序。
定理2:图灵完备
所有的图灵机都可以被一个使用$sigmoid$型激活函数的神经元构成的全连接循环网络来进行模拟,即可以实现图灵机的所有功能,解决所有的可计算问题。
循环神经网络的应用种类
序列到类别的模式
序列到序列的模型,可以理解为输入为一个$\pmb x$的序列,输出为一个表示类别的标量$\hat y$。
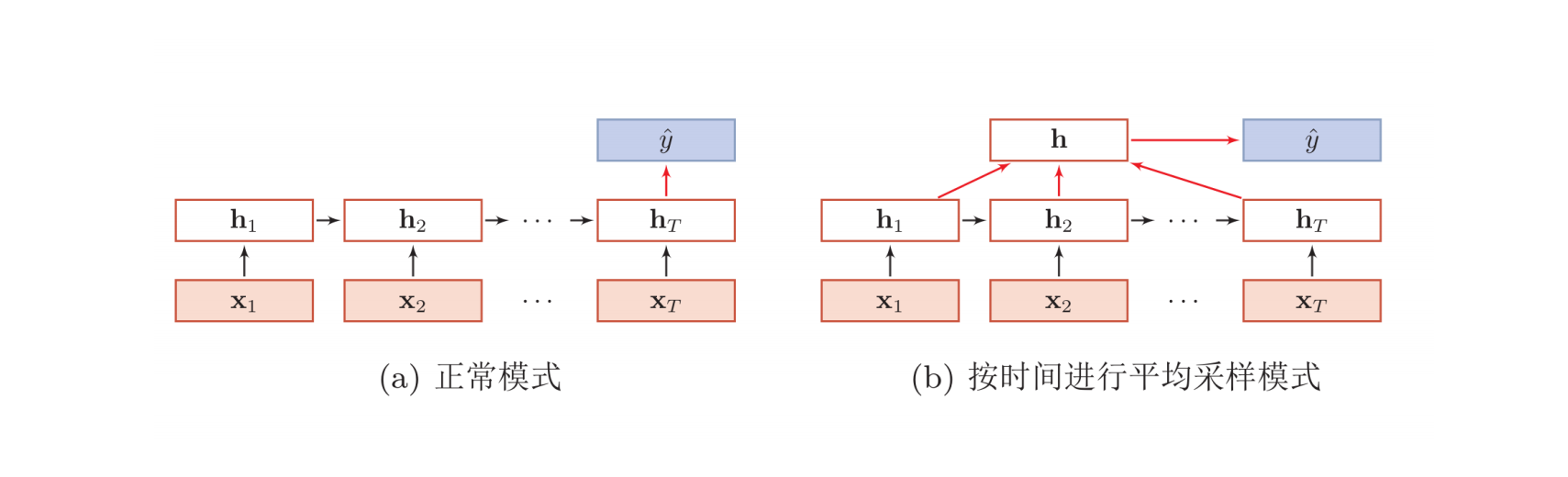
序列到类别的应用包括情感分类(文本输入到情感类别)等。
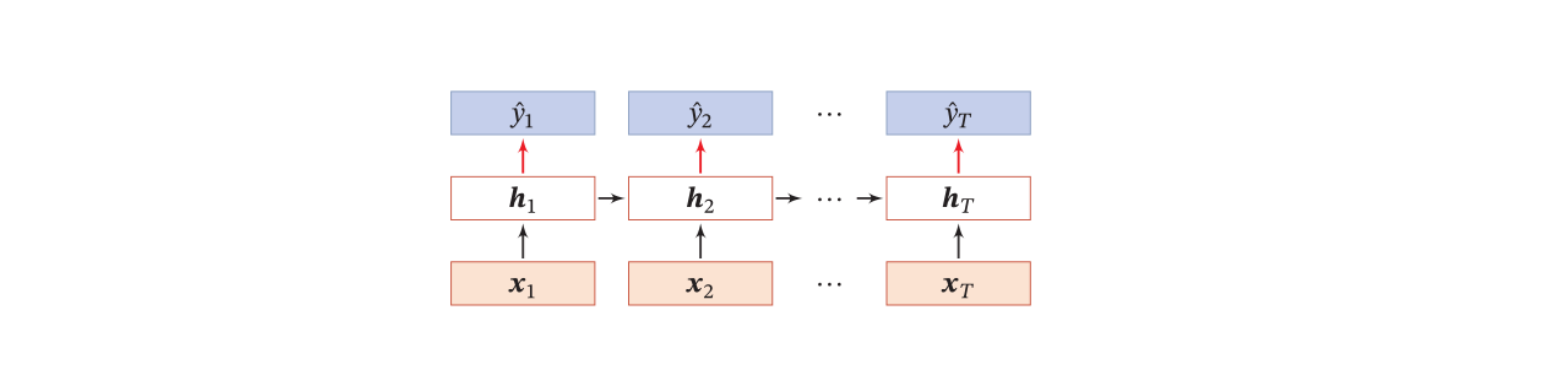
同步的序列到序列的模式
同步的序列到序列模式,输入为一个$\pmb x$的序列,输出也为一个序列$\pmb {\hat y}=[\hat y_1,\hat y_2,…,\hat y_T]$。同步的性质表示为在每个隐状态中,都是一个$\pmb x_i$经处理到输出结果$\hat y_i$。
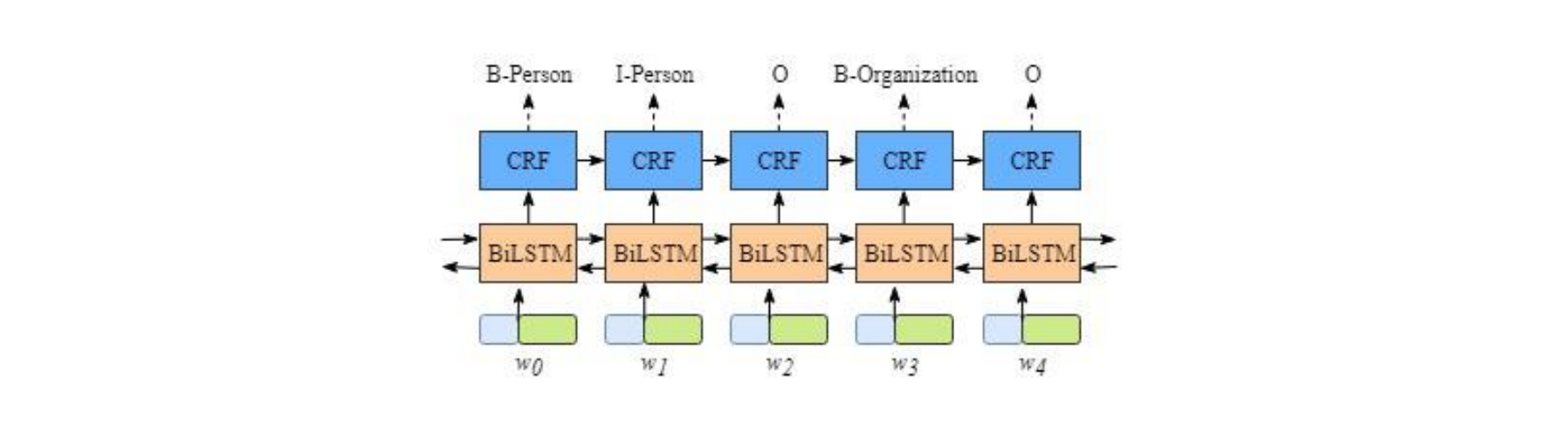
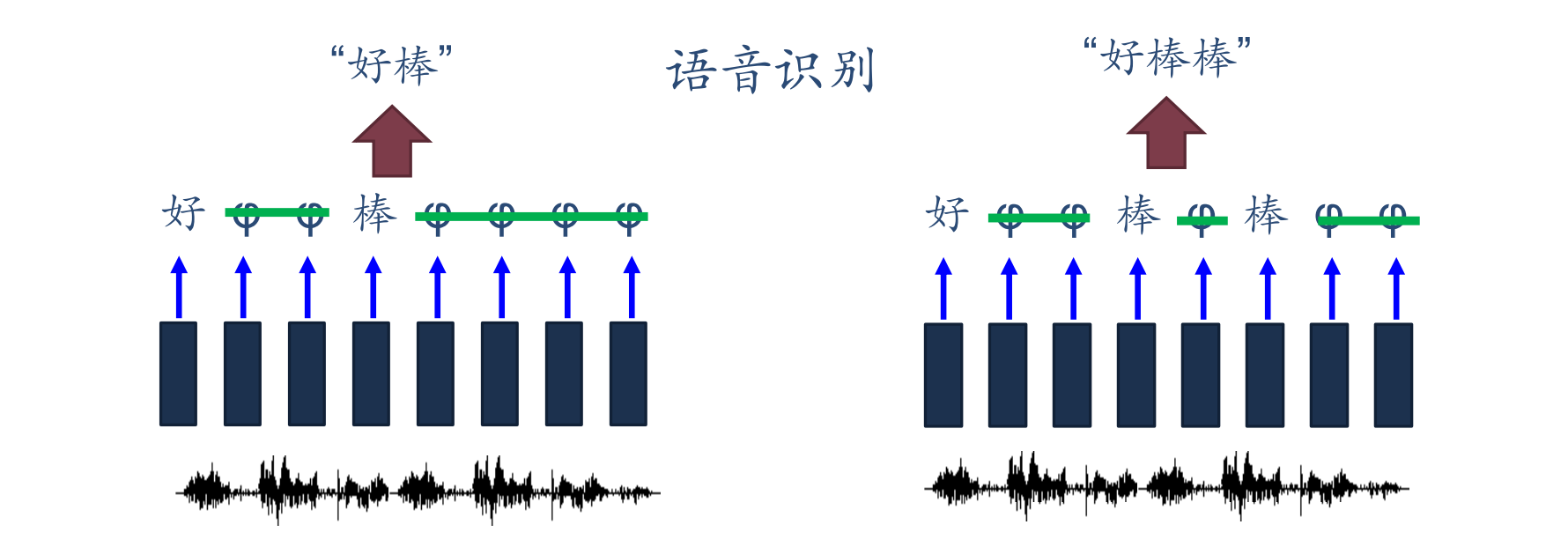
同步序列到序列的模式应用包括中文分词(文本单词输入到每个部分的位置类型输出)、信息抽取(文本单词输入到每个部分的信息类型输出)、语音识别(语音序列输入到每个子段的识别结果)等。
异步的序列到序列的模式
异步的序列到序列模式,其输入输出也均为序列,与同步的模型不同的是,异步模型的输入与输出不在同一个隐状态函数中处理,大部分都是先输入一段信息,然后开始处理,进行输出,因此这种模型一般都可以分为$Encoder$与$Decoder$部分,其中$Encoder$负责对输入的信息进行编码,形成网络可识别的数据类型;$Decoder$负责完成网络逻辑并进行输出。
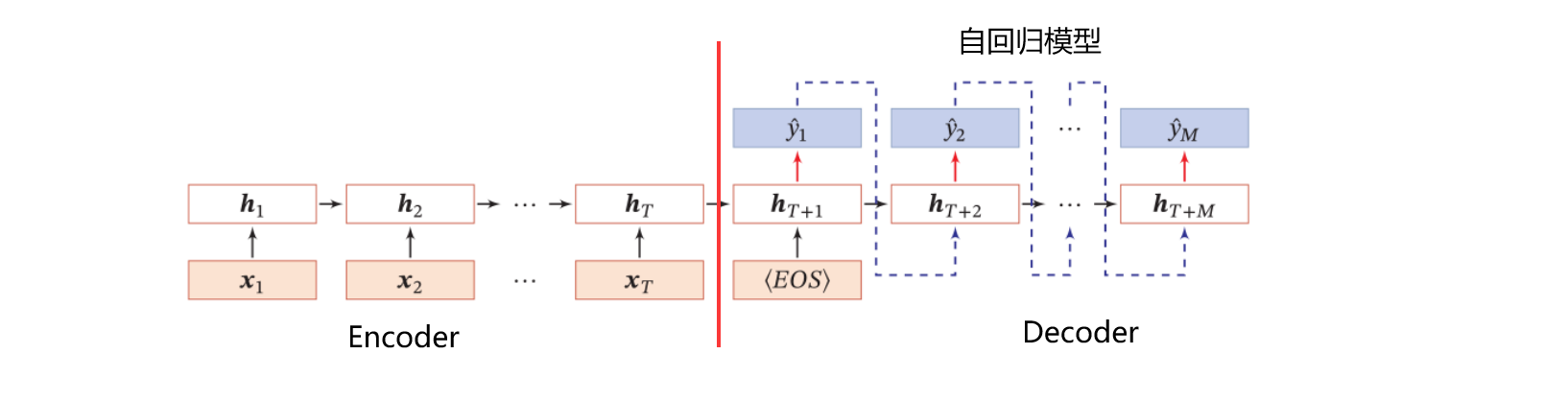
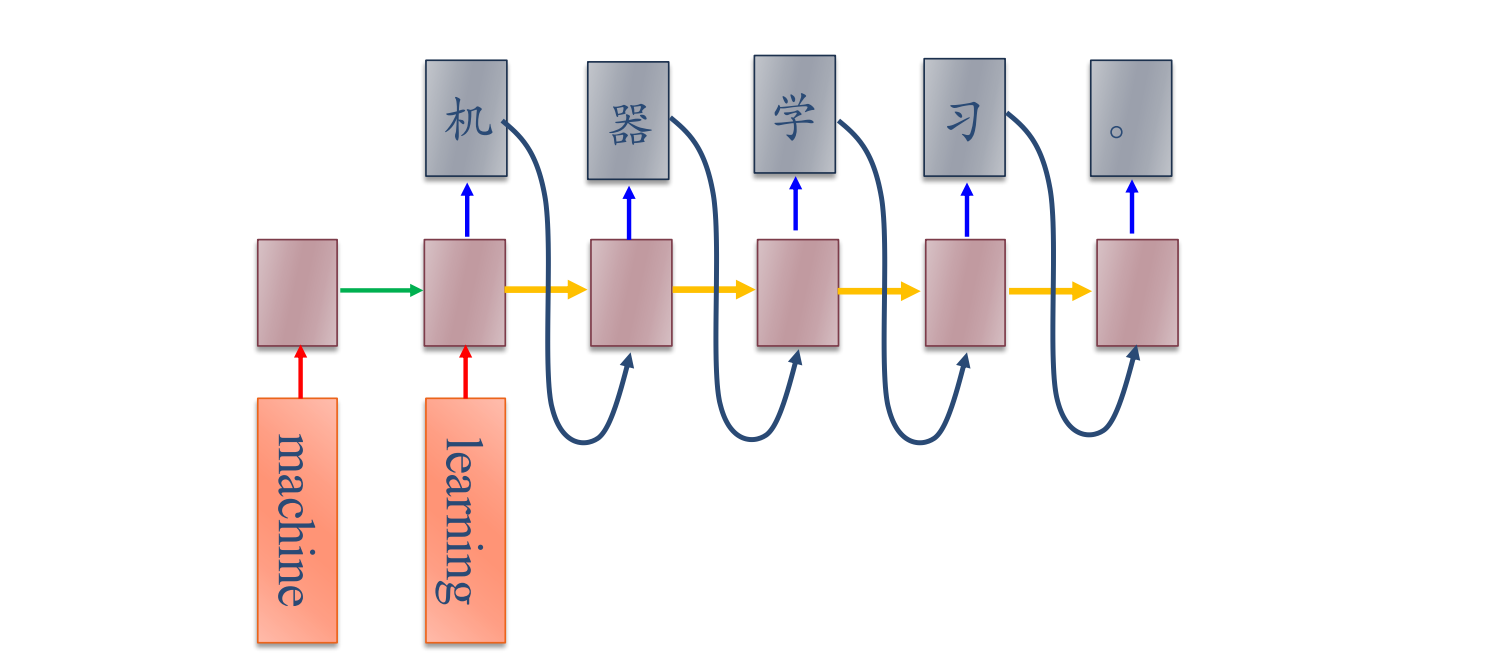
异步序列到序列的模式应用包括机器翻译(先输入文本序列,经编码后处理输出为另一段文本序列)。
参数学习与梯度
给定训练样本$\pmb{(x,y)}$,其中$\pmb x={x_1,x_2,…,x_T}$是输入序列,$\pmb y= y_1,y_2,…,y_T$是标签序列,循环神经网络在时刻$t$的瞬时损失函数可以表示为:
$$
\begin{align}
\mathcal L_t & = \mathcal L(\pmb y_t,g(\pmb h_t)) \\\\
\mathcal L & = \sum_{t=1} ^T \mathcal L_t
\end{align}
$$
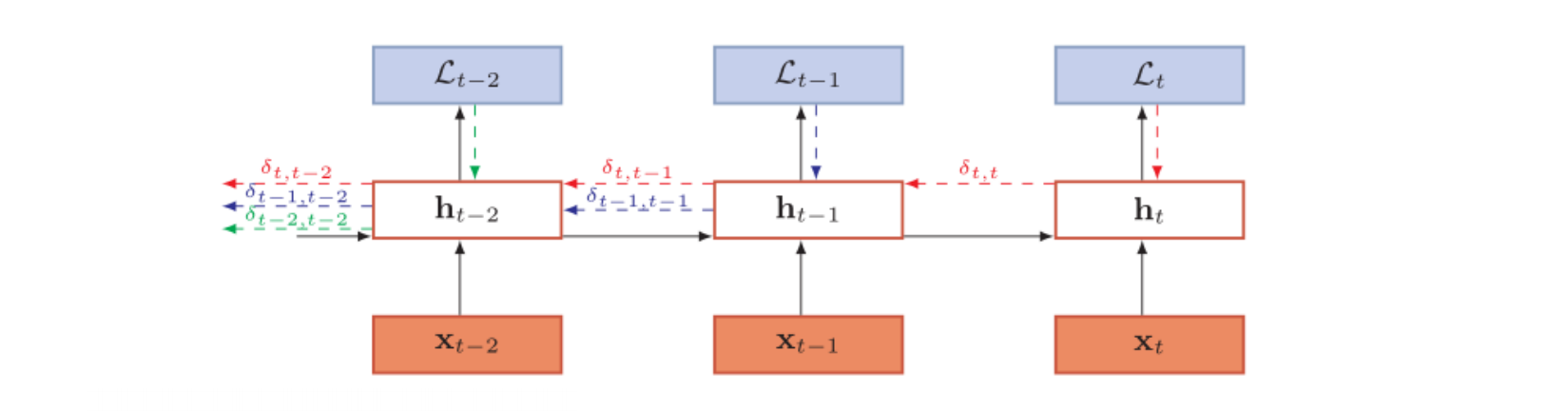
对梯度的计算可以参考反向传播算法,针对每个时刻的梯度求解,如下图:
对于简易循环神经网络,其状态转移方法如下:
$$
\pmb h_{t+1} = f(\pmb z_{t+1}) = f(U\pmb h_t + W \pmb x_{t+1} + b)
$$
其中$U,W$为超参数,每个层可能有所不同。在反向传播的过程中,$\delta_{t,k}$为第$t$时刻的损失对第$k$步隐藏神经元的净输入$z_k$的导数,即
$$
\begin{align}
\delta_{t,k} & = {\partial \mathcal L_t \over \partial z_k} \\\\
& = {\partial h_k \over \partial z_k}·{\partial z_{k+1} \over \partial h_k}·{\partial \mathcal L_t \over \partial z_{k+1}}\\\\
& = diag(f^ \prime(z_k)) U^\top\delta_{t,k+1} \\\\
& = \prod_ {\tau=k} ^{t-1}(diag(f^ \prime(z_\tau)) U^\top)\delta_{t,t}
\end{align}
$$
对于整个网络的损失梯度可以表示为:
$$
\begin{align}
\partial \mathcal L\over \partial U & = \sum_ {t=1} ^T {\partial \mathcal L_t \over \partial U} \\\\
& = \sum_ {t=1} ^T {\sum_ {k=1} ^t} {\partial \mathcal L_t \over \partial U^{(k)} } \\\\
& = \sum_ {t=1} ^T {\sum_ {k=1} ^t} {\partial \mathcal L_t \over \partial z_k}·{\partial z_k \over \partial U^{(k)} }\\\\
& = \sum_ {t=1} ^T {\sum_ {k=1} ^t} \ \delta_ {t,k}\pmb h_{k-1}^T
\end{align}
$$
对于梯度公式$\delta_{t,k} = \prod_ {\tau=k} ^{t-1}(diag(f^ \prime(z_\tau)) U^\top)\delta_{t,t}$,不妨设其中$\lambda = diag(f^ \prime(z_\tau)) U^\top$,则$\delta_{t,k} \cong \lambda^{t-k} \delta_{t,t}$。当$\lambda>1,t-k\rightarrow +\infty$时,梯度趋于无穷大,可能引发梯度爆炸问题;当$\lambda<1,t-k\rightarrow +\infty$时,梯度趋于0,可能引发梯度消失问题;由于梯度爆炸或消失问题,实际上循环神经网络只能学习到短周期的依赖关系,即长程依赖问题。
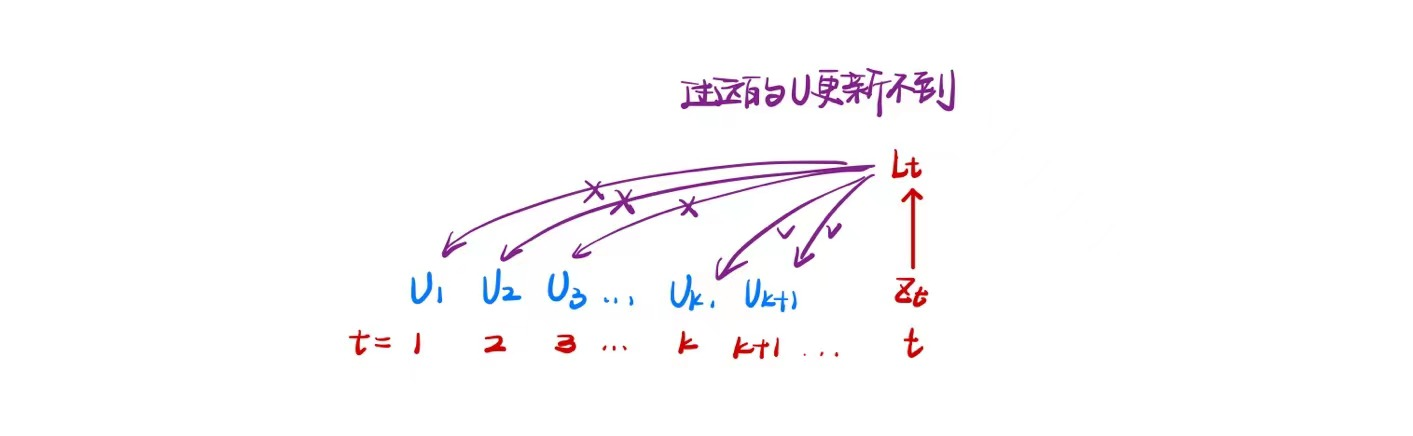
因此,要保证$\lambda$尽可能等于1。更多的,解决长程依赖问题的方法可以通过线性依赖关系、门控网络等方法解决。
线性依赖关系
将循环关系从非线性关系中摘出来。
$$
h_t = h_{t-1} + g(x_t;\theta)
$$
但这种完全摘出来的方法可能会对循环本身造成伤害,故可以增加非线性
$$
h_t=h_{t-1}+g(x_t,h_{t-1};\theta)
$$
这种表示方式就可以联想到残差网络的两路处理方法。
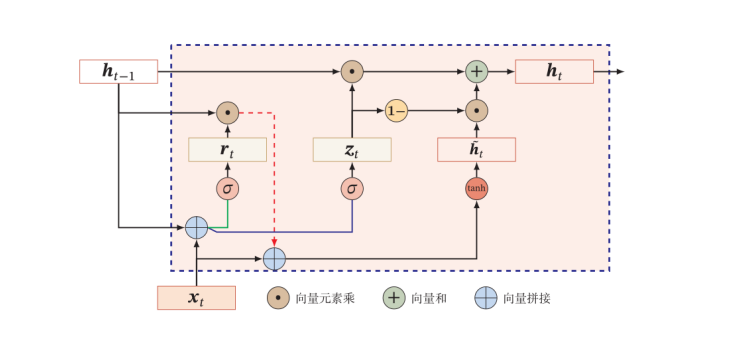
GRU(Gated Recurrent Unit)
针对于前文提到的加入非线性的线性依赖,可以继续加入门控网络,控制线性和非线性部分的比重,提高灵活性
$$
h_t= z_t\odot h_{t-1} + (1-z_t)\odot g(x_t,h_{t-1};\theta),\ z_t\in(0,1)^d,\ d=Dim(h_t)
$$
其中$z_t$是门控部分,若$z_t=1$则遗忘$h_{t-1}$,取非线性部分;若$z_t=0$则遗忘非线性部分,取$h_t = h_{t-1}$,当然上述是加入门控的一种思路,实现比这要复杂许多。
更多的,由于线性依赖中的非线性关系$g(x_t,h_{t-1};\theta)$是包含记忆单元$h_{t-1}$的,因此可以类似于$z_t$的思路将$h_{t-1}$前面加上一个门控$r_t$,即可得到$GRU$门控循环网络的两个主要门控。
$$
\begin{align}
\pmb {\hat h_t} & = tanh( W_c \pmb x_t+ U(\pmb r_t \odot \pmb h_{t-1})+\pmb b_n) \\\\
\pmb h_t & = \pmb z_t\odot \pmb h_{t-1} + (1-\pmb z_t)\odot \pmb {\hat h_t}
\end{align}
$$
对于两个门控,本身也可以用线性组合过非线性函数来实现。
$$
\begin{align}
重置门: \pmb r_t = \sigma(W_r \pmb x_t+ U_r \pmb h_{t-1}+ \pmb b_r) \\\\
更新门: \pmb z_t = \sigma(W_z\pmb x_t+ U_z\pmb h_{t-1}+ \pmb b_z)
\end{align}
$$
LSTM(Long Short-Term Memory)
基于GRU的门控思路,可以在最后输出时再加入一个输出门,用于控制输出与否和输出的强度,即网络表示为:
$$
\begin{align}
\pmb {\hat c_t} & = tanh(W_c \pmb x_t+ U_c\pmb h_{t-1}+\pmb b_c) \\\\
\pmb c_t & = \pmb f_t\odot \pmb c_{t-1} + \pmb i_t\odot \pmb {\hat h_t} \\\\
\pmb h_t & = \pmb o_t \odot tanh(\pmb c_t)
\end{align}
$$
其中每个门也都可以使用输入$x_i$和历史记忆$h_{i-1}$表示。
$$
\begin{align}
输入门: \pmb i_t & = \sigma(W_i\pmb x_t+ U_i\pmb h_{t-1}+ \pmb b_i) \\\\
遗忘门: \pmb f_t & = \sigma(W_f\pmb x_t+ U_f\pmb h_{t-1}+ \pmb b_f) \\\\
输出门: \pmb o_t & = \sigma(W_o\pmb x_t+ U_o\pmb h_{t-1}+ \pmb b_o)
\end{align}
$$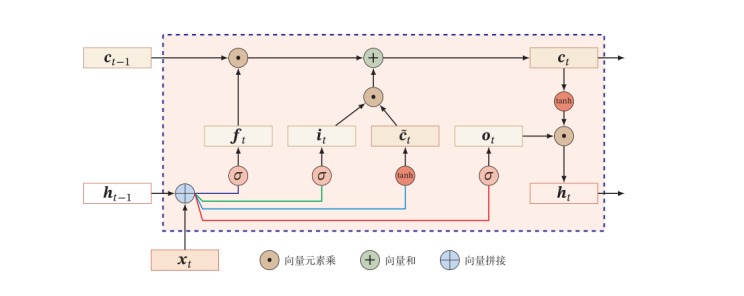
LSTM根据使用的门控不同,其也有许多派生的种类,如没有遗忘门:$\pmb c_t = \pmb c_{t-1}+ \pmb i_t \odot \pmb {\hat c_t}$;耦合输入门和遗忘门:$\pmb f_t+\pmb i_t = 1$等。
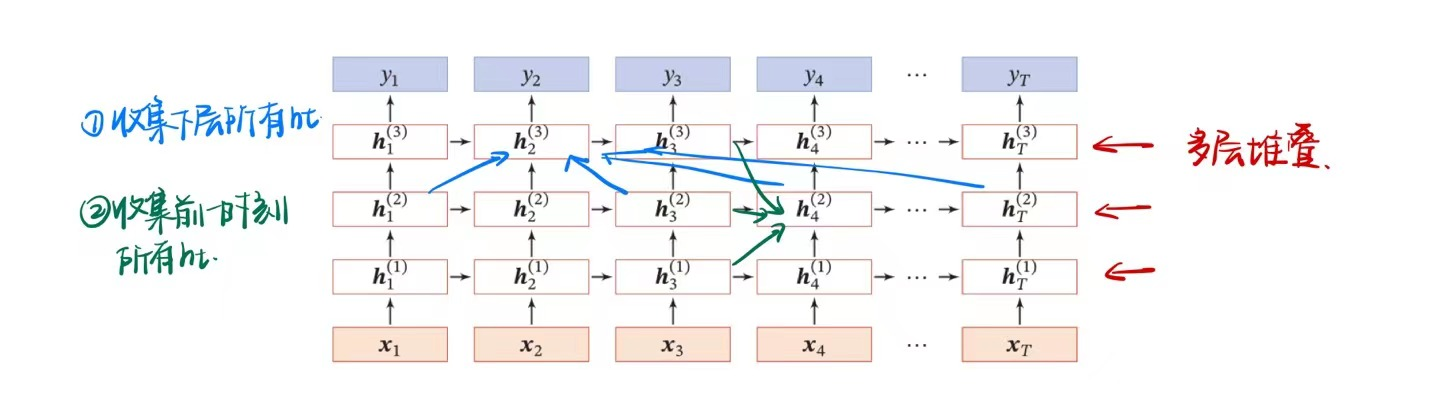
深层模型(非时间维度上的加深)
堆叠神经网络
在非时间维度上堆叠多层$h$非线性层。
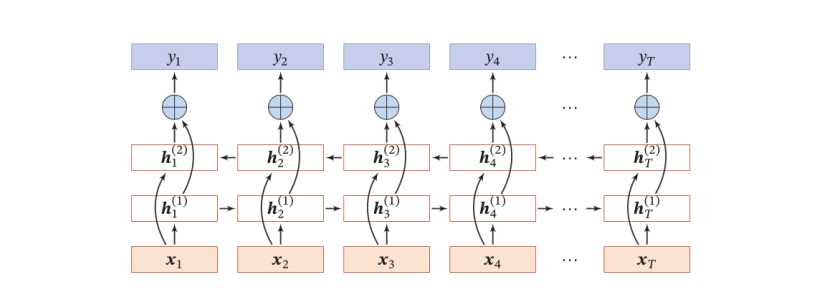
双向神经网络
使用双向的隐含状态
非序列模型
递归神经网络
被指向结点使用指向节点的多个状态信息。
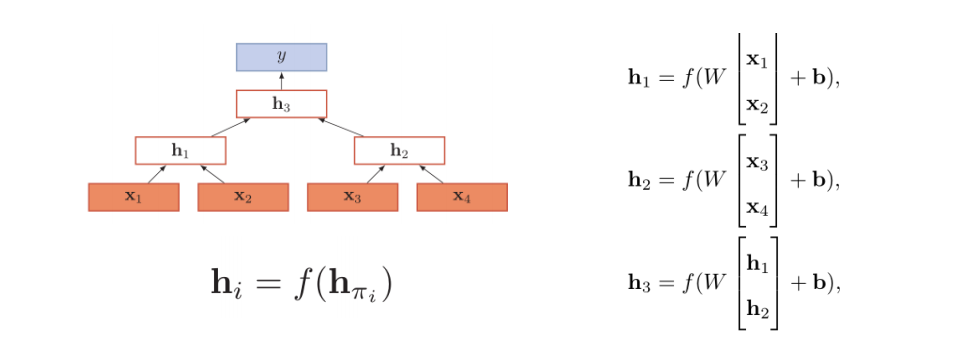
图神经网络
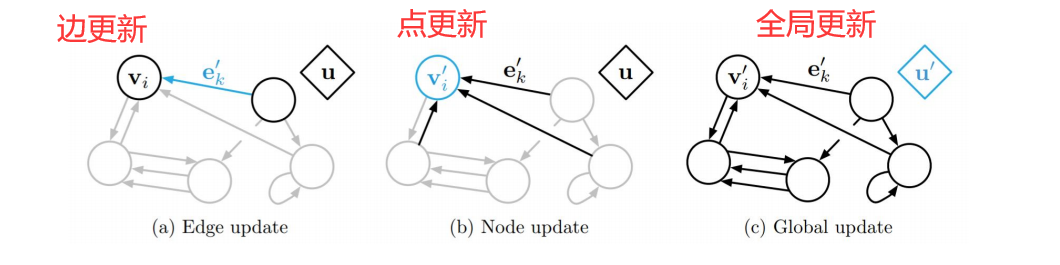
对于一个任意的图结构$G(V,E)$,可以得
更新函数:
$$
\begin{align}
\pmb m_t ^{(v)} = \sum_{u\in N(v)} f(\pmb h_{t-1} ^{(v)},\pmb h_{t-1} ^ {(v)}, \pmb e^{(u,v)}) \\\\
\pmb h_t ^{(v)} = g(\pmb h_{t-1} ^{(v)},\pmb m_t ^{(v)})
\end{align}
$$
读出函数
$$
\pmb y_t = g({h_T ^{(v)} | v \in \mathcal V})
$$
其他应用
语言生成模型
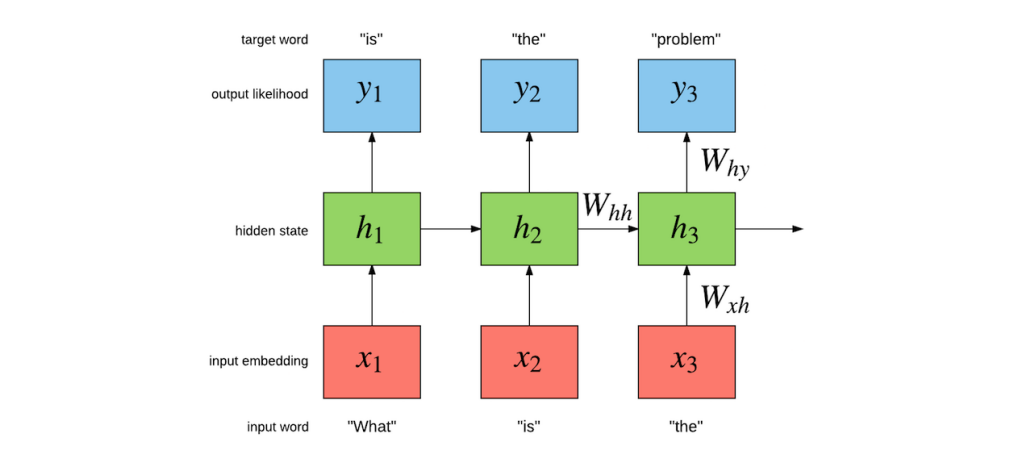
序列到序列的机器翻译
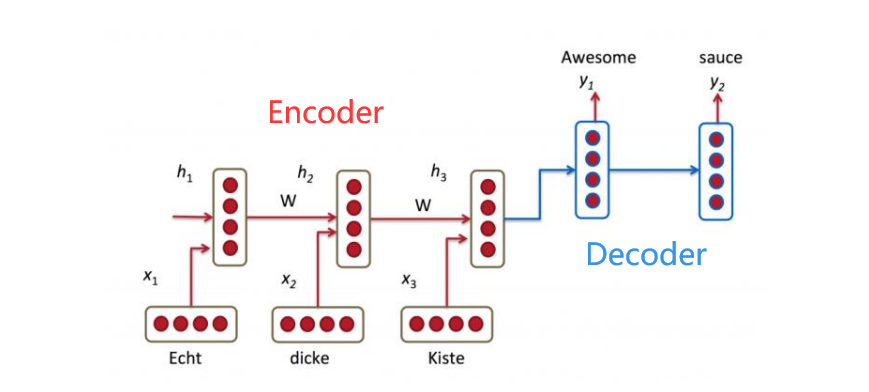
对话系统
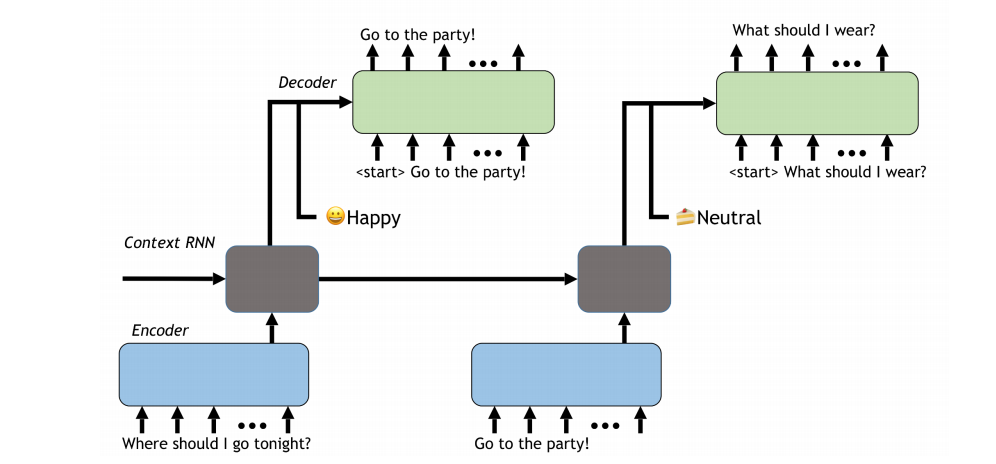
总结
优点
- 引入记忆环节,提高时序的利用效率
- 图灵完备,可拟合任意一个程序单元
缺点
- 长程依赖问题$\rightarrow GRU/LSTM$
- 记忆容量问题$\rightarrow 遗忘门$
- 并行能力,时间依赖