CS224N课程P5：语言模型和循环神经网络RNN

课程词汇

magnitude - 大小；量级
consecutive - 连续的
granularity - 粒度
incoherent - 不连贯的
subtlety - 微妙之处；巧妙
chug - 一饮而尽；一次性处理
thrall - 使成为奴隶；受奴役的

课程内容

网络优化与正则化

正则化

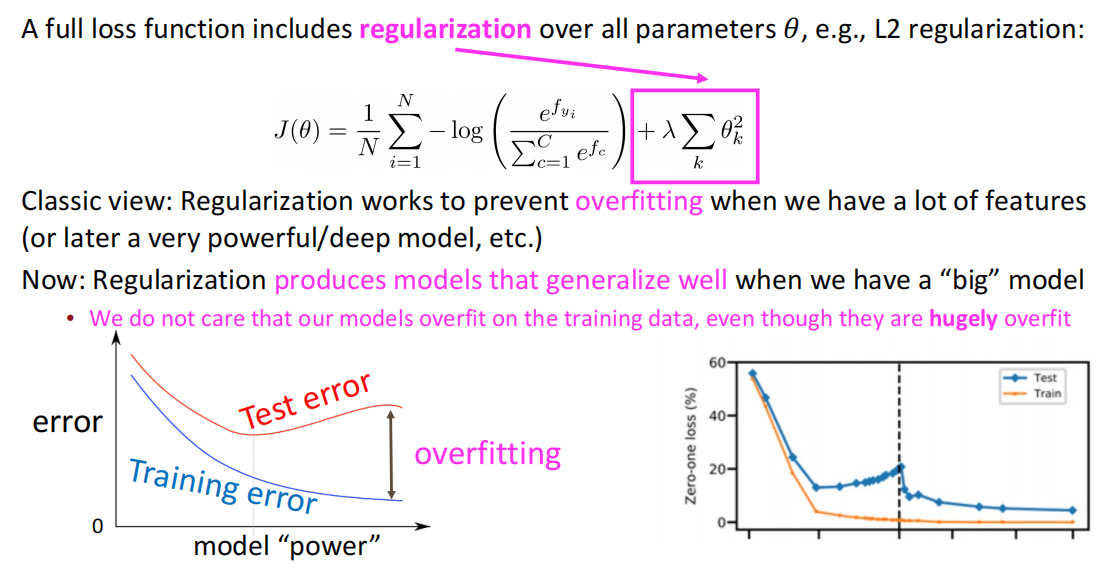
一个完整的损失函数一般会包含一个正则化项，用于降低模型过拟合程度：

Dropout

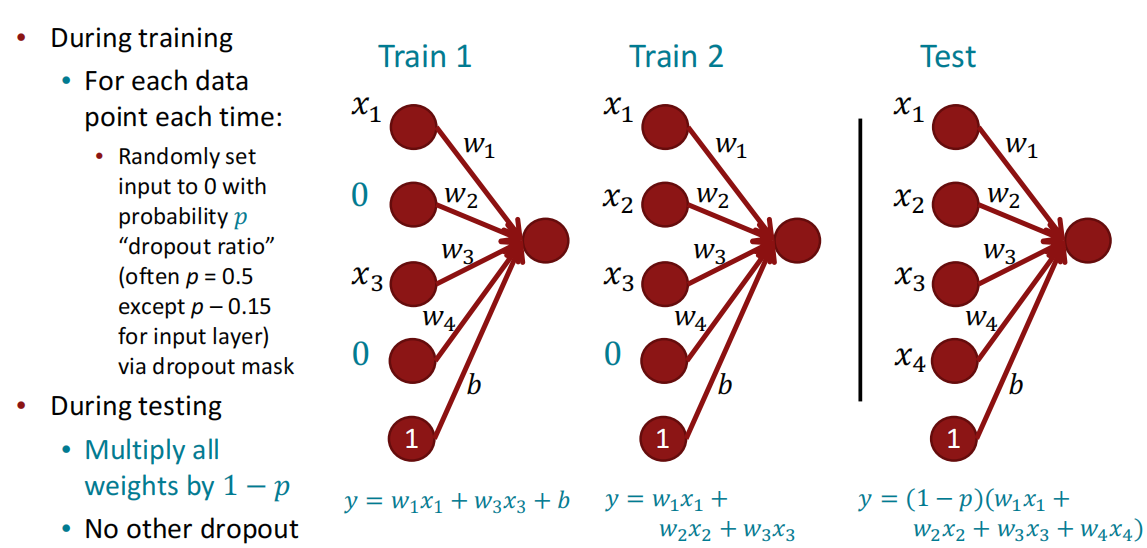
参见[网络优化与正则化笔记 - Ywj226]。Dropout可以有效解决因特征依赖导致的特征的不完全性。

非线性函数

参数初始化

常用的参数初始化方法是将权重设置为(-r,r)的均匀分布，且不能将其设置为0矩阵，防止出现对称问题，但是偏置bias从经验来说是可以置0的。现有的初始化方法中，还有根据扇入扇出的规模做初始化的Xavier方法。

优化方法和学习率

参见[网络优化与正则化笔记 - Ywj226]。

语言模型和RNN

语言模型的定义为：预测下一个单词是什么的任务；如输入法的智能推荐，搜索引擎的下拉框，都是语言模型的具体应用。更为正式的，定义语言模型的形式如下：给定一个单词序列$x^{(1)},x^{(2)},…,x^{(T)}$，此段文本的出现概率为：
$$
P(x^{(1)},…,x^{(T)})=P(x^{(1)}) \times P(x^{(2)}|x^{(1)})\times …\times P(x^{(T)}|x^{(T-1)},…,x^{(1)}) = \prod_{t=1}^T P(x^{(t)}|x^{(t-1)},…,x^{(1)})
$$
其中$x^{(t)}$可以是词汇$V=\lbrace w_1,…,w_{|V|}\rbrace$中的单词，最后的$P(x^{(t)}|x^{(t-1)},…,x^{(1)})$就是语言模型的概率表示。我们也可以将语言模型理解为对一段文本出现的概率做估计或推断。

n-gram语言模型

典型的对语言模型的学习可以通过学习一个n-gram语言模型来实现。一个n-gram是n个连续单词所形成的组(chunk)，如：

对n-gram的出现频率做计算，可以有效的预测下一个单词是什么，也是思路比较简单的做法。n-gram模型基于马尔可夫独立假设：$x^{(t+1)}$的预测只基于前面的$n-1$个单词。所以语言模型的概率表示可以等价为：

在n-gram模型中，我们可以将概率问题用计数代替，而由于特定的n-gram的块在语料中出现频率极少甚至为0，其可能会导致模型的稀疏性，即绝大部分的概率为零，这会降低模型本身的效果。针对于此，在分子和分母上的稀疏性做简要改进：

• 分子上：平滑技术，在每个单词$w\in V$的计数上加上一个小值$\delta$，防止其置0；
• 分母上：回退技术，将(n-1)-gram回退成(n-2)-gram,…直到分母不为零（unigram）。

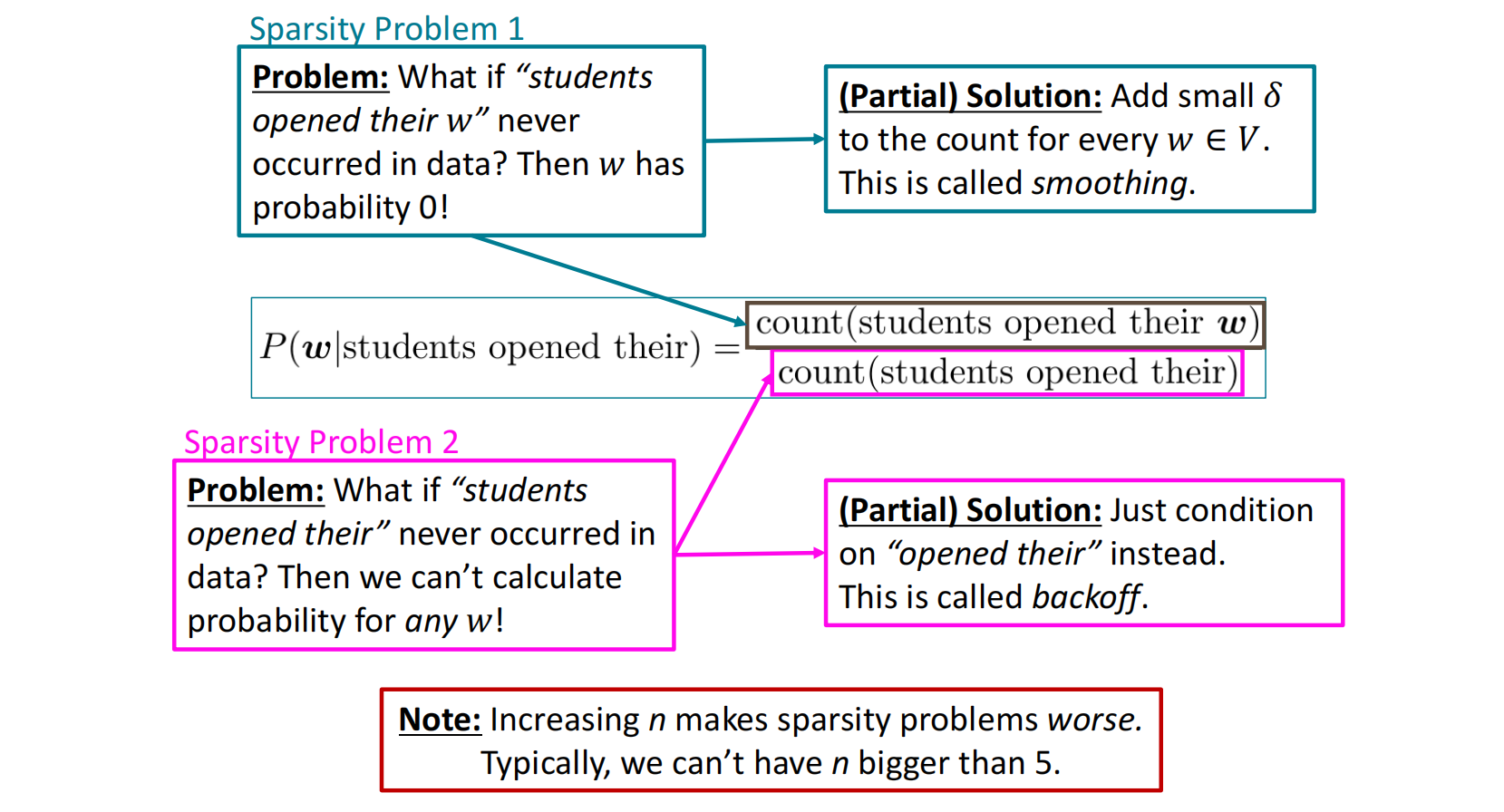
在n-gram中，由于语言模型的概率基于n-gram的计数，因此模型需要存储在语料中的所有n-gram的数量，这个存储规模是很大的，而且增加n-gram的n和增加语料规模都会大幅增加存储。

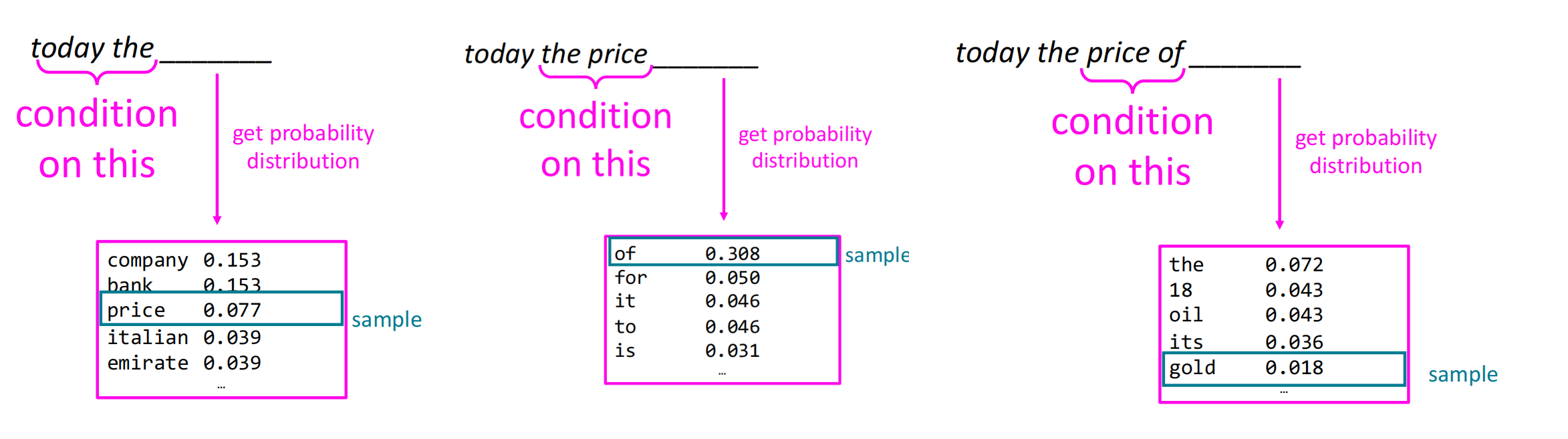
n-gram的工作流程为，每次移动到一个n-gram块，获取下一次单词的概率分布并从中采样（采样结果可能不是概率最大的单词），逐个往下预测直到句子结束或遇到结束符。使用n-gram生成的文本一般在语法上有很惊人的效果，但在连贯性上有所缺点。

神经网络语言模型

基于窗口的神经网络模型

将n-gram的每个块作为一个窗口，放到基于窗口的神经网络模型中训练相对位置关系。

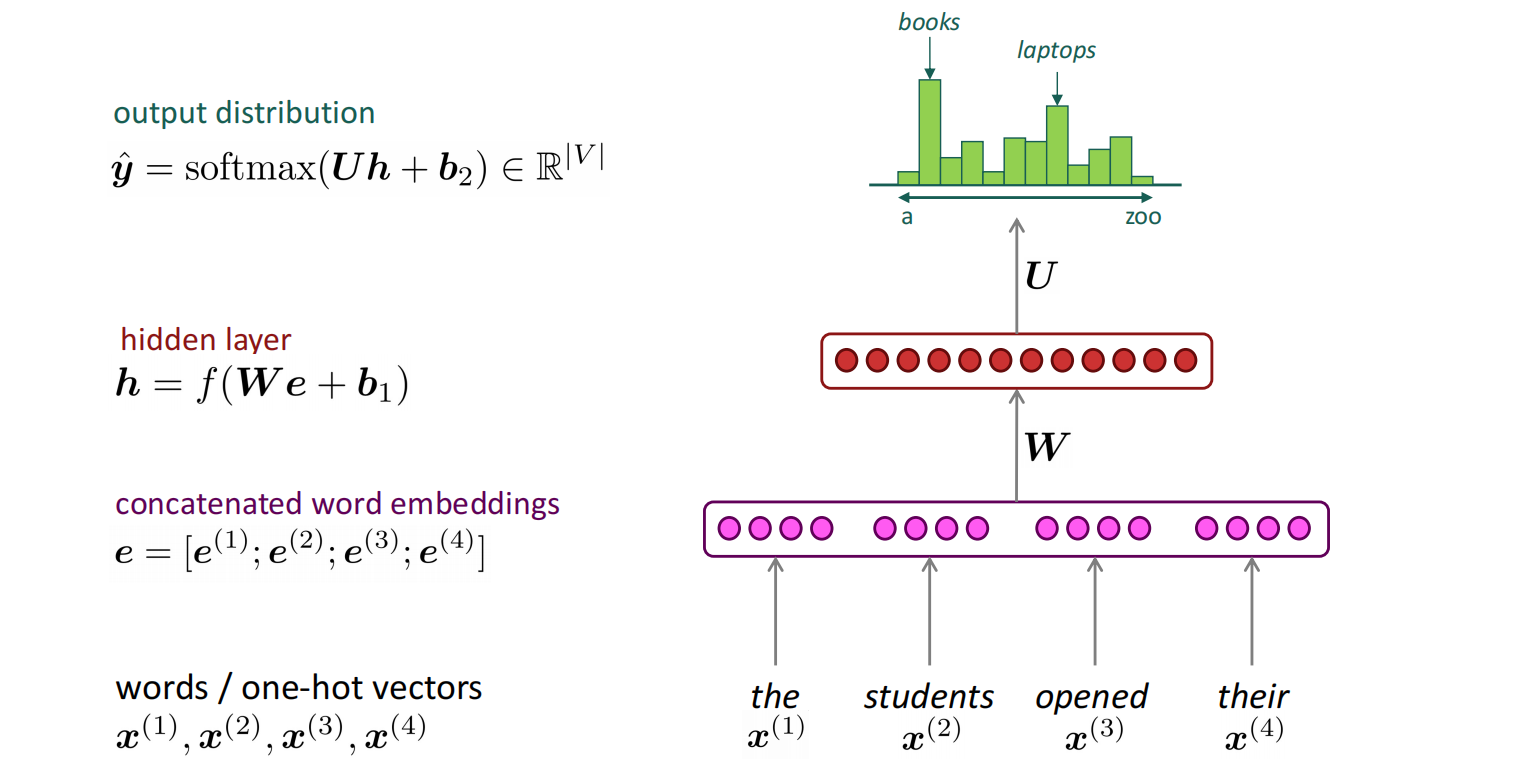
固定窗口的网络模型可以解决n-gram稀疏的问题和存储的问题，但因为窗口固定，其固定涉及到的范围较小，且更改窗口大小需要一起扩大权重$W$的维度，且是平方级增大；在固定窗口中由于不同位置的权重不同，存在因位置导致的不对称的问题，$x^{(1)}$和$x^{(2)}$乘以完全不同的权重，输入的处理不对称。

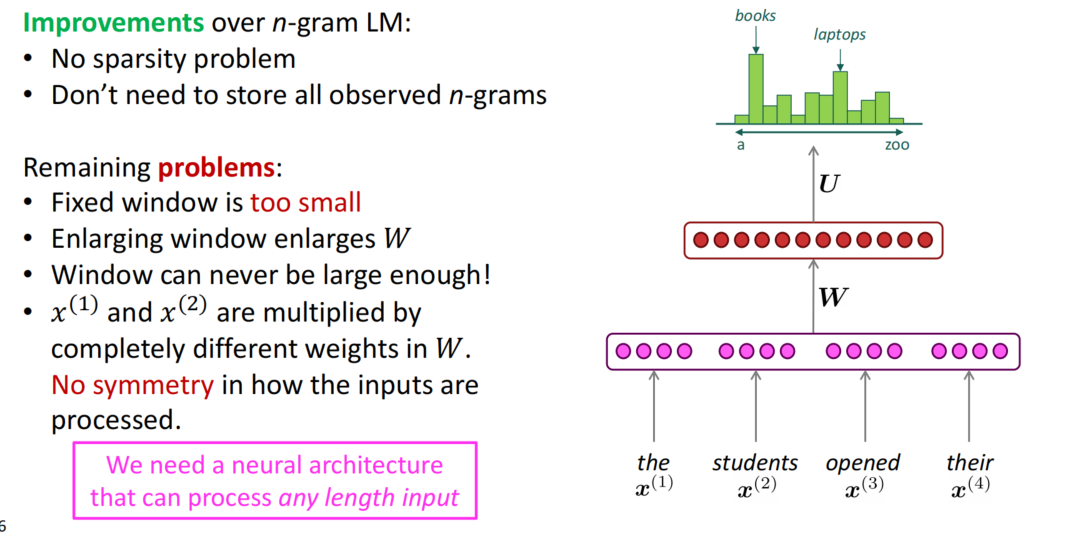
循环神经网络RNN（Recurrent Neural Network）

一个简单的RNN语言模型架构图如下：

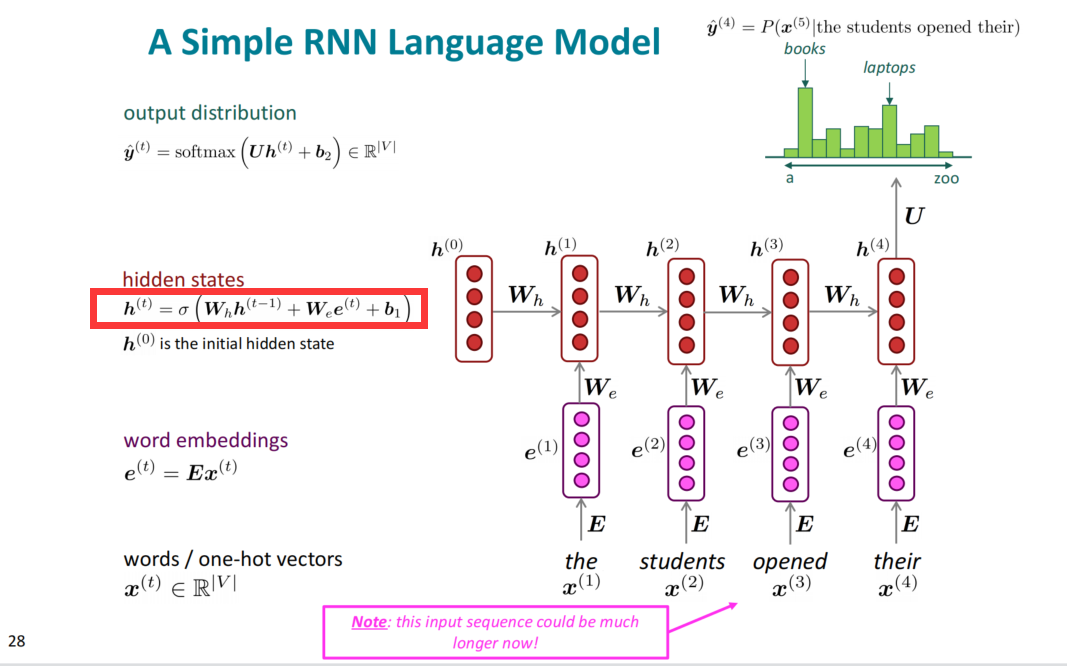
单词离散向量经词嵌入之后，需要过一个从头到尾的一个模型，模型的每个隐状态由当前词和历史隐状态组成。

RNN大致解决了固定窗口神经网络的问题，但是由于速度和实际用起来的一些问题，简单RNN还需要有所优化。

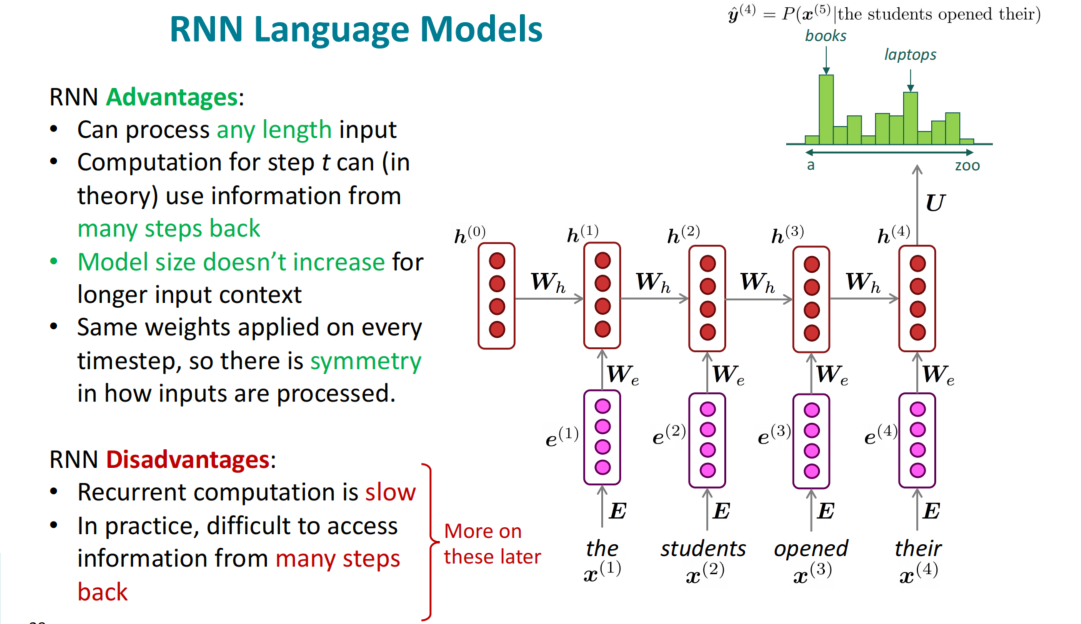
RNN语言模型的训练

给定一个大规模的语料，将其喂到RNN-LM中，在每个时间步$t$计算其计算输出分布，在第$t$步的损失函数是预测概率分布$\pmb {\hat y}^{(t)}$和真实的下一个单词$\pmb y^{(t)}$（$\pmb x^{(t+1)}$的one-hot向量）的交叉熵：
$$
J^{(t)}(\theta)= CE( \pmb y^{(t)},\pmb {\hat y}^{(t)} ) = -\sum_{ w\in V }\pmb y_w^{ (t) } \log \pmb { \hat y }_ w^{(t)} = -\log \pmb{\hat y}_ {\pmb x_{ t+1} }^{(t)}
$$
模型的总体损失是对每个$t$的损失加和：
$$
J(\theta) = {1 \over T}\sum_{t=1}^T J^{(t)}(\theta) = {1 \over T}\sum_{t=1}^T -\log \pmb{ \hat y }_ {\pmb x_ {t+1} }^{(t)}
$$

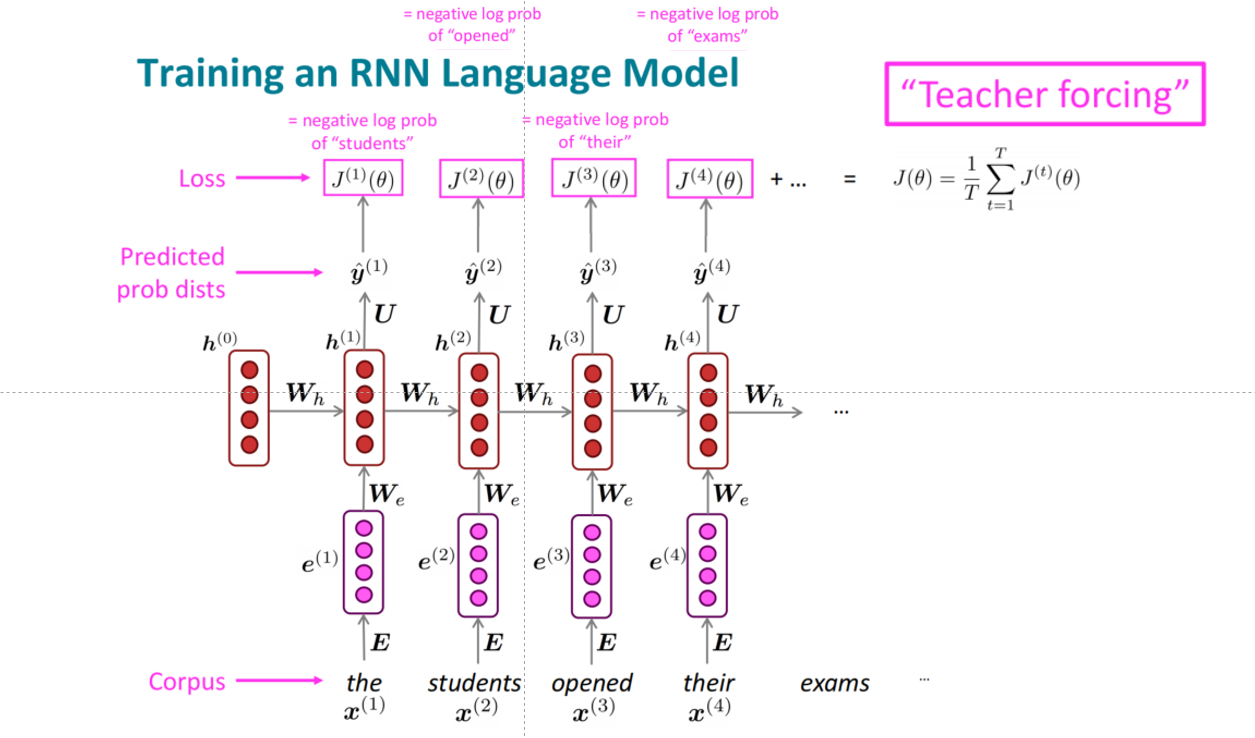
训练RNN的整理流程就是从左到右按照每个时刻$t$分别获得预测概率，计算与下一个单词的损失loss，最后其加和就是总的loss，需要注意的是：

1. 在实际训练中，句子的前后都会加上开始标记[start]和结束标记[end]
2. 这里用到了Teacher Forcing的技巧，与Free-Running相对应，其训练方式有所不同：Free-Running不会干扰模型的训练过程，每次生成的单词作为下一步的单词输入；而Teacher Forcing每次的输入都是句子里对应位置的单词，而非模型生成，以防止模型因之前的错误影响后面的训练。

例如：Mary is watching you.输入[start]，模型训练得到第一个单词为"a"，原序列第一个单词为"Mary"。
Free-Running过程会直接将其作为下一步的输入，即下一步输入"a";
Teacher-Forcing会记录当前的惩罚loss，并将原来的下一个单词作为输入，即下一步输入"is"。

在计算RNN的损失和梯度时，每次都需要计算一次，在对整个语料一次性计算的过程，其时间和空间代价都十分的昂贵，实际上操作时，会将$\pmb x^{(1)},…,\pmb x^{(T)}$看作一组句子或一组文档，并参照随机梯度下降的思路，每次只随机的采用一个或一个batch的句子计算损失和梯度，更新参数，这样就可以降低RNN的计算难度。

以上的过程主要通过前向过程计算了模型的损失，同样的，模型也需要后向的过程以计算梯度。

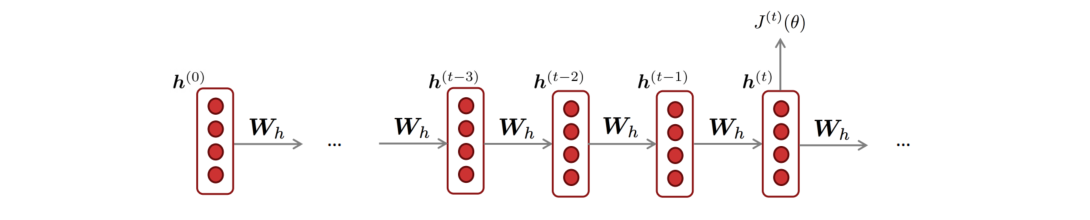
问题在于如何计算关于重复的权重矩阵$W_h$的偏导数$J^{(t)}(\theta)$，其答案和loss一样，同样是对每个时间步$i$的偏导做加和：
$$
{ {\partial J^{(t)} } \over {\partial \pmb W_h } }= \sum_{i=1}^t { {\partial J^{(t)} } \over {\partial \pmb W_h } } \bigg|_{(i)}
$$
整体梯度等于每个时间$i$的梯度加和，其推导过程就是链式法则中的分叉过程，对每段进行加和：

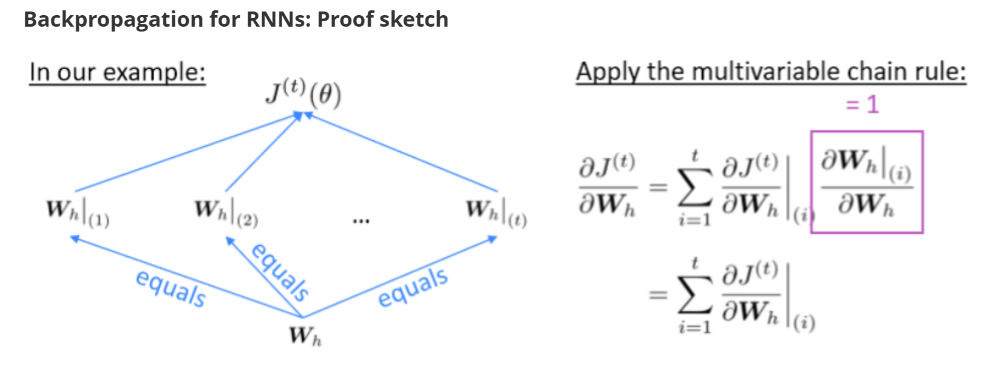
而梯度的合理计算过程就是从模型最后的时刻$t$开始反向传播，每次传播计算一次梯度，将其加到总和中，反向传播到最开始，即可以计算出整体的梯度值。需要注意的是，实际上反向传播的过程中会应用截断的技巧，将反向传播的步数限制在~20，这样就可以更为有效的实现传播和梯度的计算，梯度的值也不会有过多的影响。

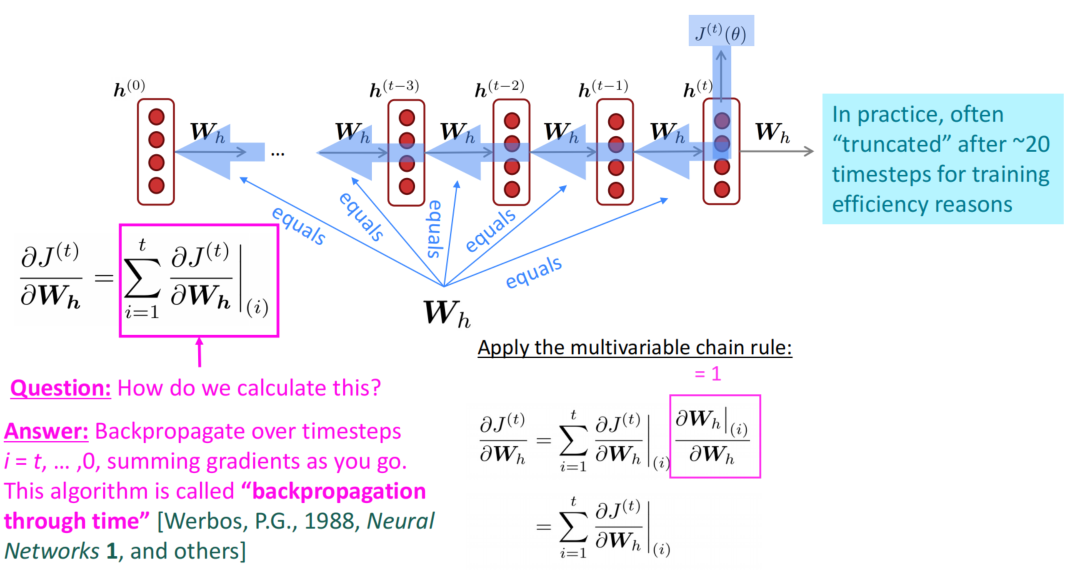
语言模型的评估

语言模型的标准评估指标是困惑度(perplexity)。

困惑度的表达式和交叉熵损失$J(\theta)$的指数幂是一致的，越小的困惑度代表其表现越好。
$$
\prod_{t=1}^T \left( {1 \over {\pmb {\hat y}_ {\pmb x_{t+1} }^{(t)} } }\right) ^{1/T} = \exp \left( {1\over T} \sum_{t=1}^T-\log \pmb{\hat y}_ {\pmb x_{t+1}^{(t)} } \right) = \exp(J(\theta))
$$
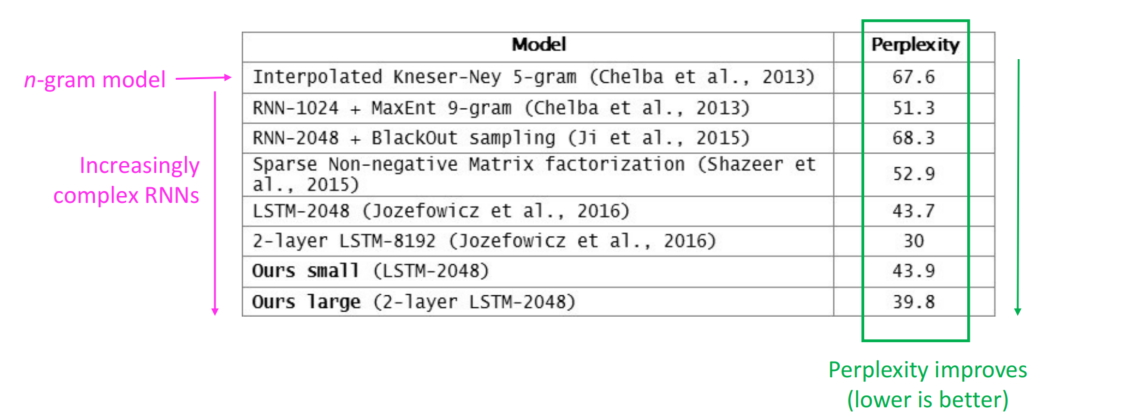
目前已有的模型中，LSTM在困惑度评估中的表现相对比较好，因为语言中有一些固定情况是没办法准确预测下一个单词的（如something指代的是什么），因此困惑度一般都会有20左右的起底。

梯度消失与梯度爆炸

梯度消失

在反向传播的梯度计算中，当梯度的数值比较小时，随着梯度的传播，这些小值会通过乘积变得越来越小，以导致反向传播的后面的神经元，其接收到的梯度会及其小，过小的梯度会导致参数更新放缓甚至不更新，从而使长文本的更新失效。

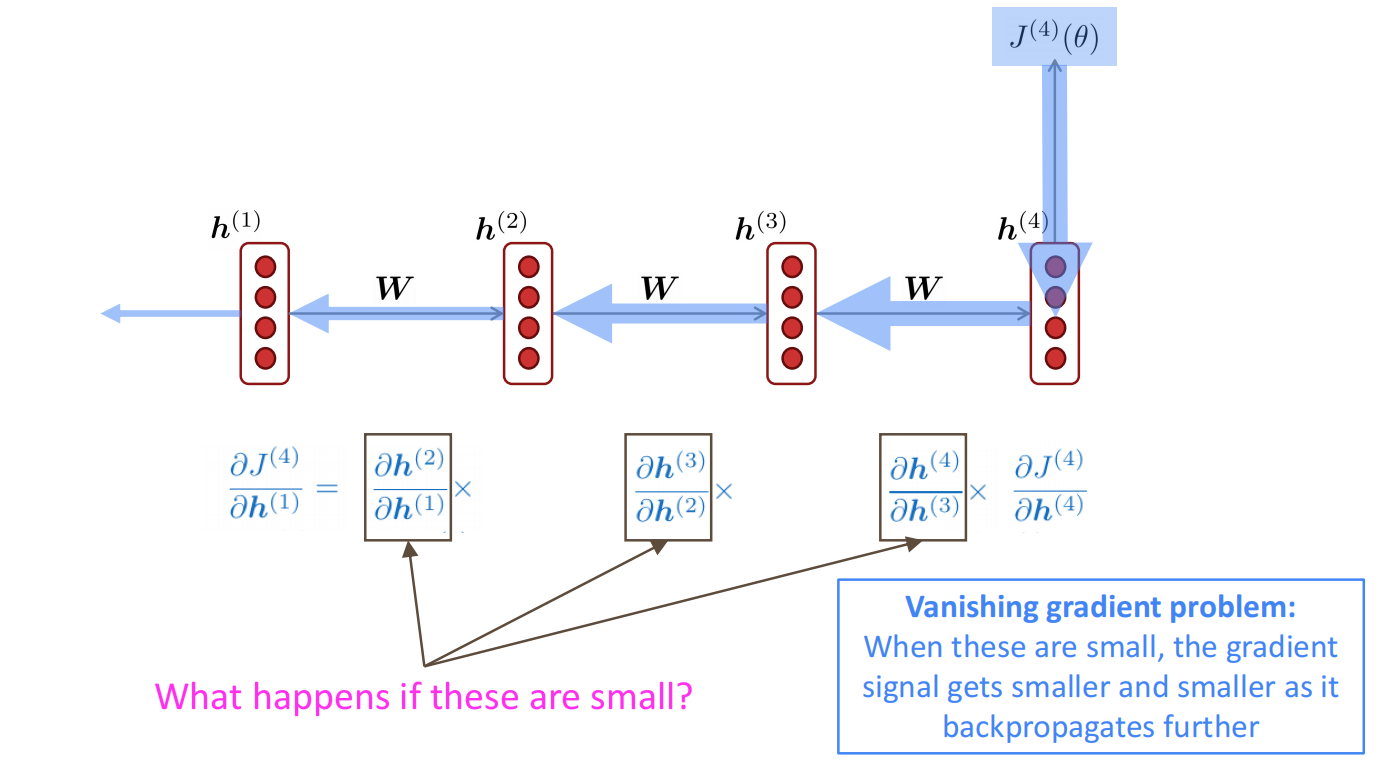
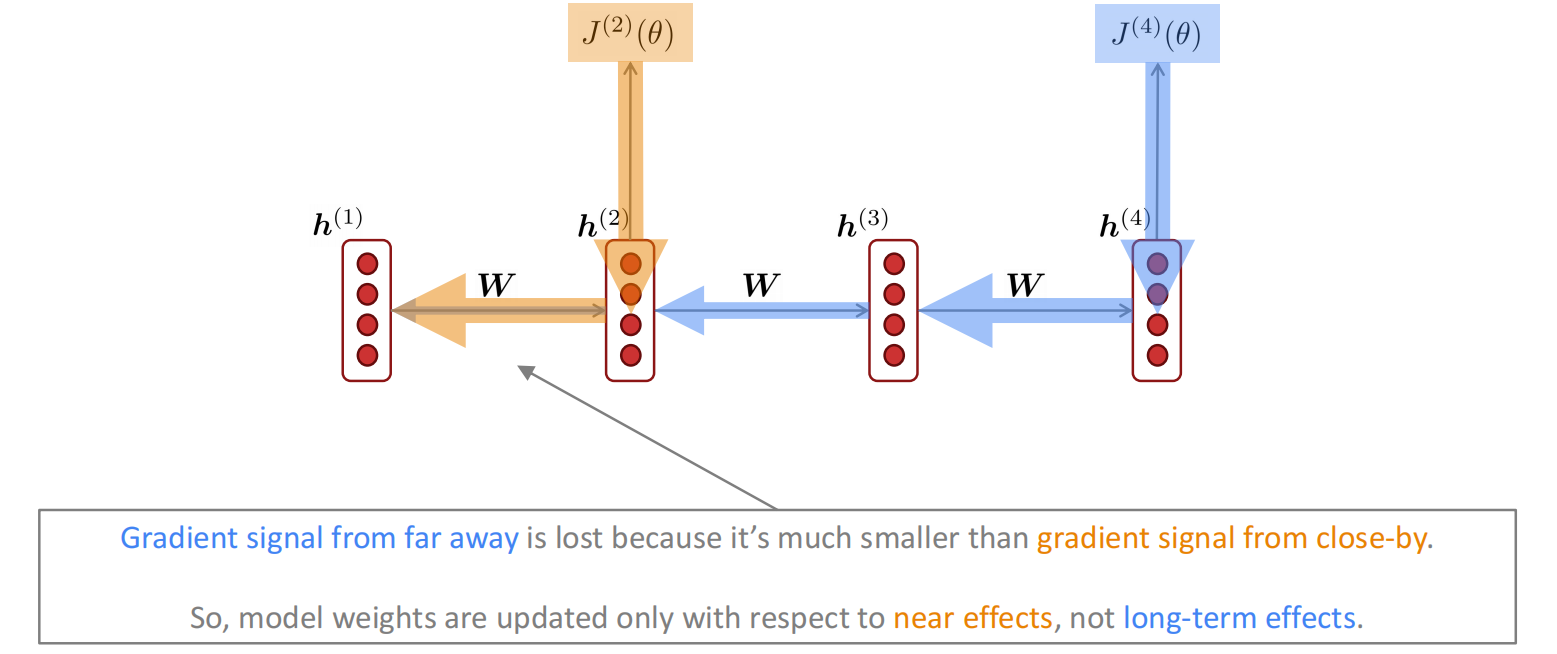
梯度消失的简要证明如下：

首先，RNN的隐状态公式为：
$$
\pmb h^{(t)} = \sigma\left(\pmb W_h\pmb h^{(t-1)}+\pmb W_x \pmb x^{(t)}+\pmb b_1 \right)
$$
考虑将非线性消去，即$\sigma(x)=x$，则有
$$
\begin{align}
{ {\partial \pmb h^{(t)} } \over {\partial \pmb h^{(t-1)}} } & = {\rm diag} \left( \sigma’ \left(\pmb W_h\pmb h^{(t-1)}+\pmb W_x \pmb x^{(t)}+\pmb b_1 \right)\right )\pmb W_h \\ & = \pmb {I\ W}_ h = \pmb W_ h
\end{align}
$$
考虑损失函数$J^{(i)}(\theta)$在第$i$步的梯度，对于在前面第$j$步的隐状态$\pmb h^{(j)}$，令$l = i-j$
$$
\begin{align}
{ {\partial J^{(i)}(\theta)} \over {\partial \pmb h^{(j)}} } & = { {\partial J^{(i)}(\theta)} \over {\partial \pmb h^{(j)}} } \prod_{j\le t\le i} { {\partial \pmb h^{(t)}} \over {\partial \pmb h^{(t-1)}} } \\
& = { {\partial J^{(i)}(\theta)} \over {\partial \pmb h^{(i)}} } \prod_{j\le t\le i} \pmb W_h \\
& = { {\partial J^{(i)}(\theta)} \over {\partial \pmb h^{(i)}} } \pmb W_h^l
\end{align}
$$
如果$\pmb W_h$很小，则经过$l$次乘积之后，这个乘积会趋近于极小，从而导致梯度消失问题。这个“很小”的评价可以用特征值，考虑$\pmb W_h$的特征值全部都小于1（充分不必要条件），即有$\lambda_1,…,\lambda_n < 1$，对应特征向量为$\pmb q_1,…,\pmb q_n$，我们可以将上面的结果写作特征表示：
$$
{ {\partial J^{(i)}(\theta)} \over {\partial \pmb h^{(i)}} } \pmb W_h^l = \sum_{i=1}^n c_i \lambda_i^l\pmb q_i \approx 0
$$
对于非线性映射$\sigma$，对上述的推理逻辑没有影响，除了需要证明$\lambda_i < \gamma$。

梯度爆炸

如果梯度变得过大，随机梯度下降的更新步会变得非常大，这可能会导致梯度摆荡甚至可能收敛到一个无效位置（如INF或NaN），进而导致网络收敛变慢或无法收敛的情况。
$$
\theta_{new}= \theta_{old}-\alpha\nabla_{\theta}J(\theta)
$$
针对于梯度爆炸的问题，可以采取梯度截断的办法，设定一个梯度的阈值，当梯度超过既定的阈值则将其裁剪，相当于原方向继续走一步，但是走相对小的一步，防止梯度爆炸情况出现。

实际上，梯度裁剪是一个十分重要的细节，但梯度爆炸是一个相对比较容易解决的问题。

RNN生成文本

使用RNN的过程也可以应用到文本生成的任务中，具体来说，从开始标记<s>训练，每个timestep会生成下一个单词的概率分布，对每个timestep做一次sample，然后将sample的结果放到下一个timestep训练，直至遇到结束标记</s>，将生成的单词连成句子，就大致实现了文本的生成过程。使用这种过程就可以大致实现风格化的文本生成，如生成一个哈利波特风格的文本段落等等，还蛮有趣的。

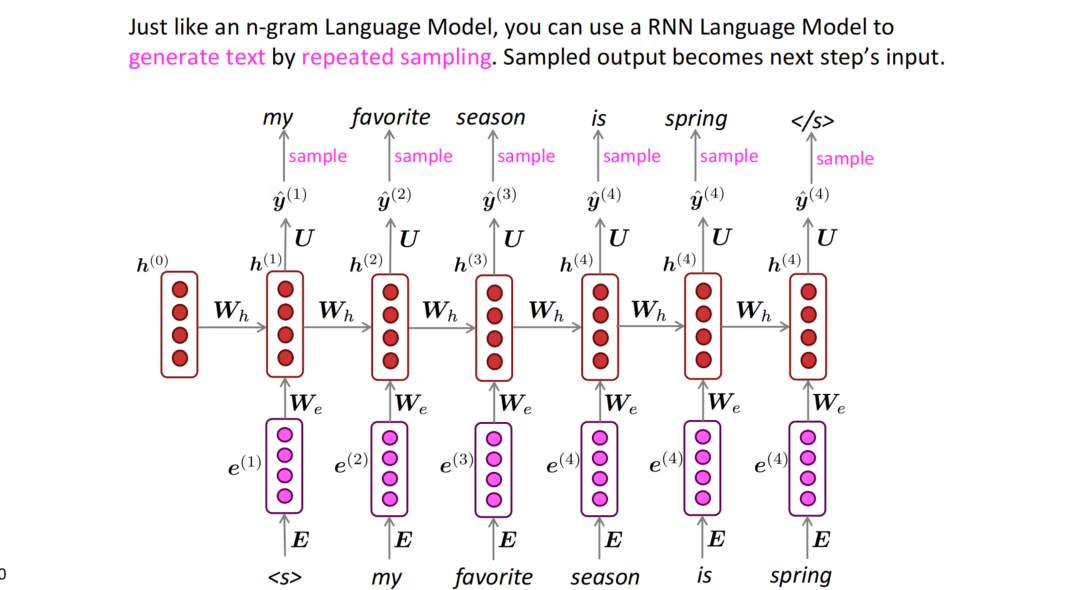
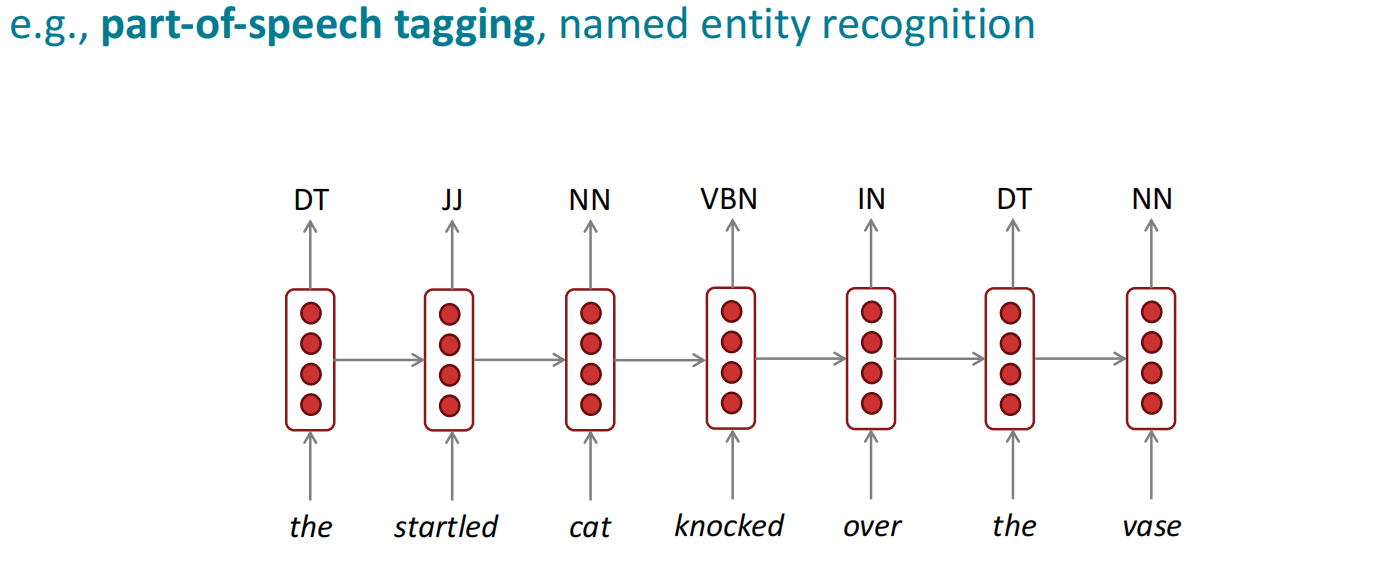
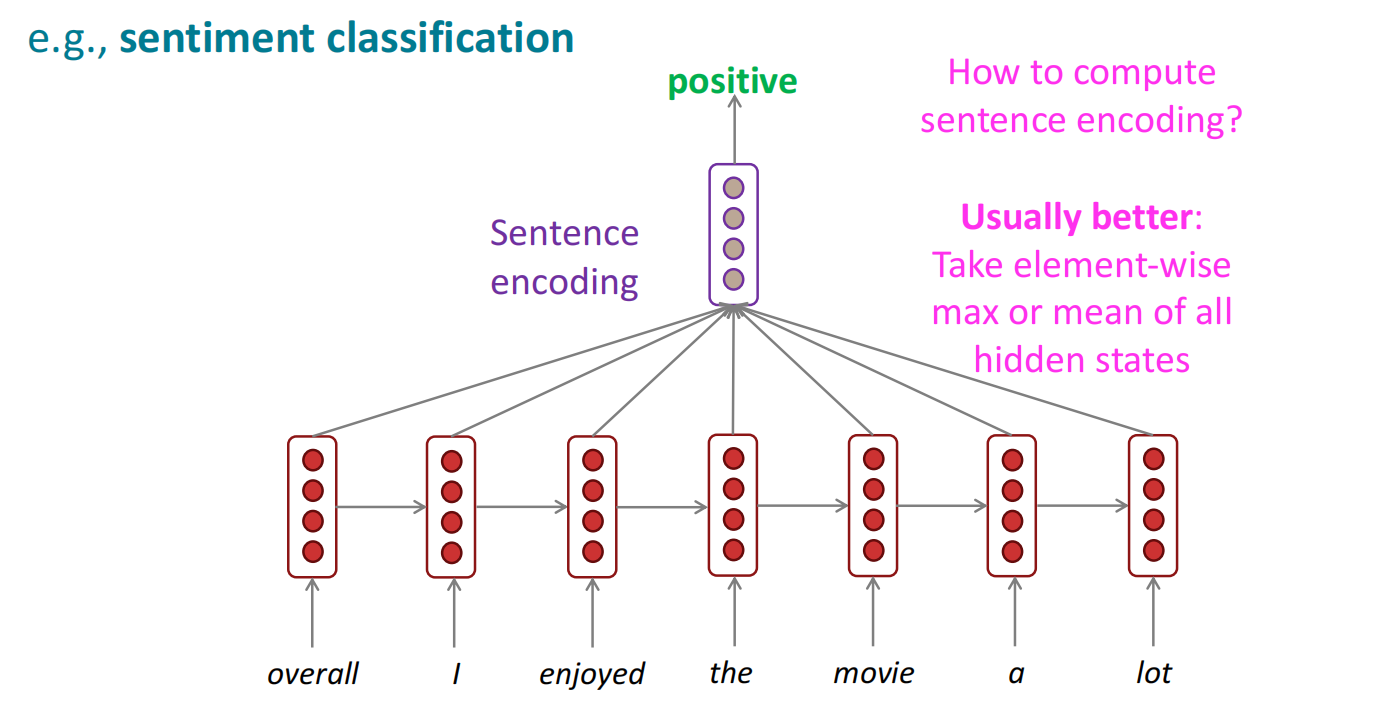
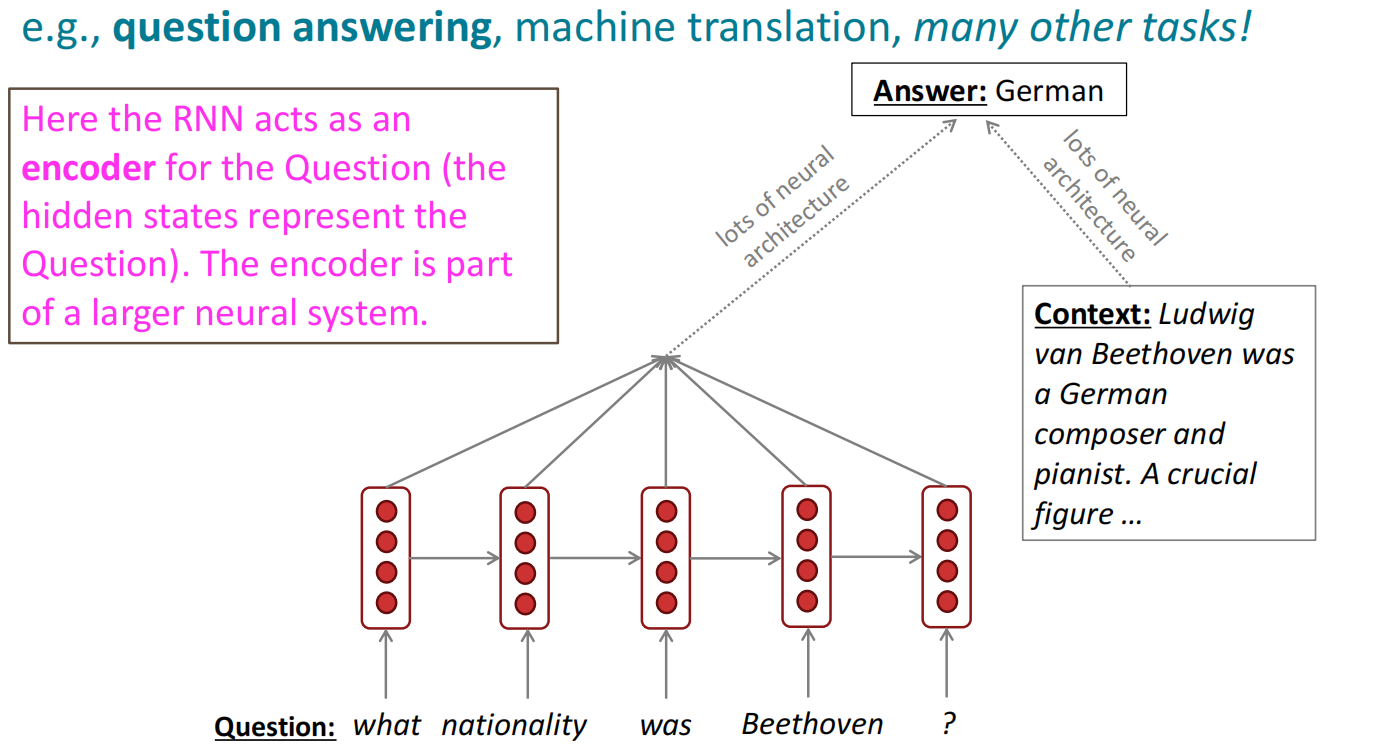
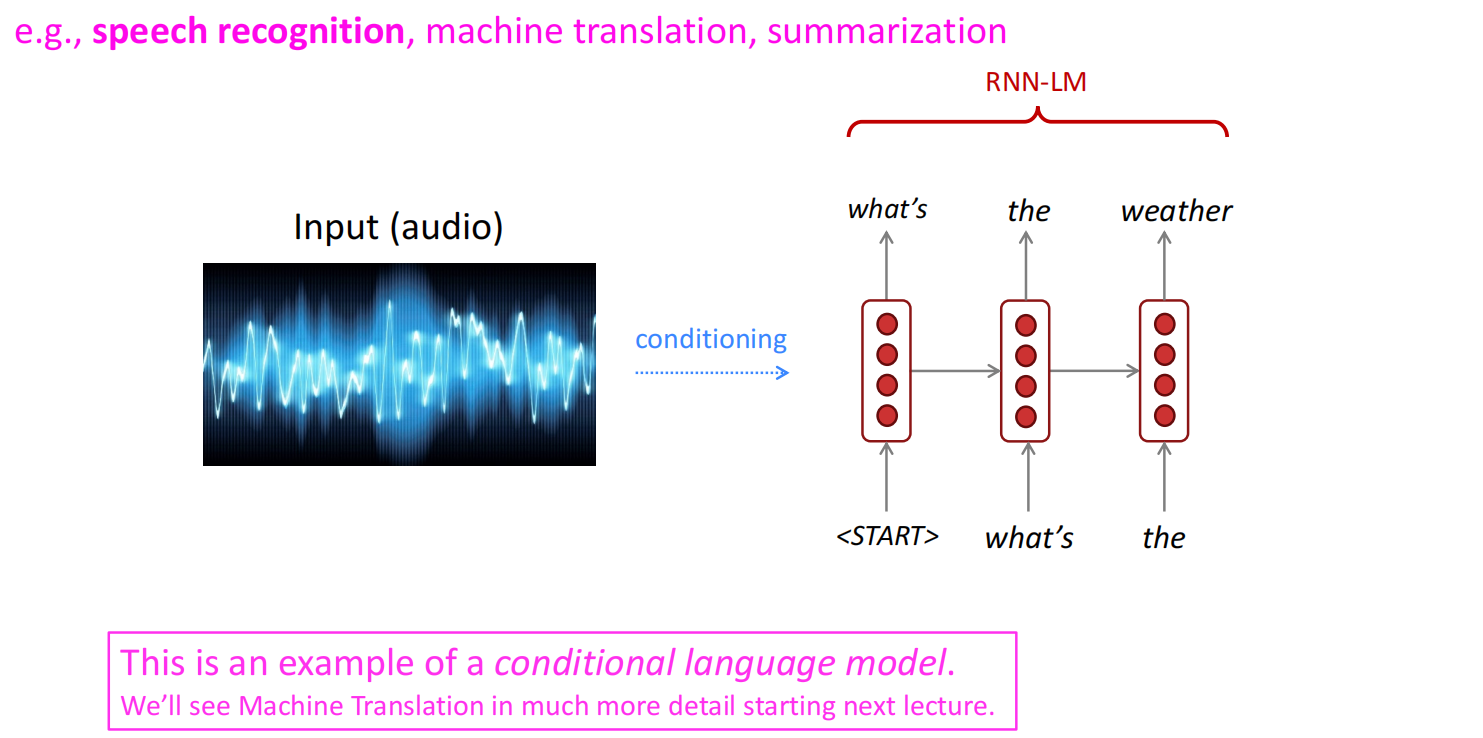
RNN的应用

课后问题