CS224N课程P3:反向传播和神经网络
本文最后更新于:几秒前
课程词汇
1 | |
课程内容
用神经网络实现NER(命名实体识别)

主要逻辑是通过人工标注的数据训练逻辑分类器,根据窗口中单词向量的连接对每个类的中心单词{yes/no}进行分类

具体过程大致可以分为:
- 设置窗口,将每个窗口的单词组成矩阵,如窗口为$+2,-2$,则$x\in \mathbb R^{5d},d\ is\ the\ num\ of\ words$;
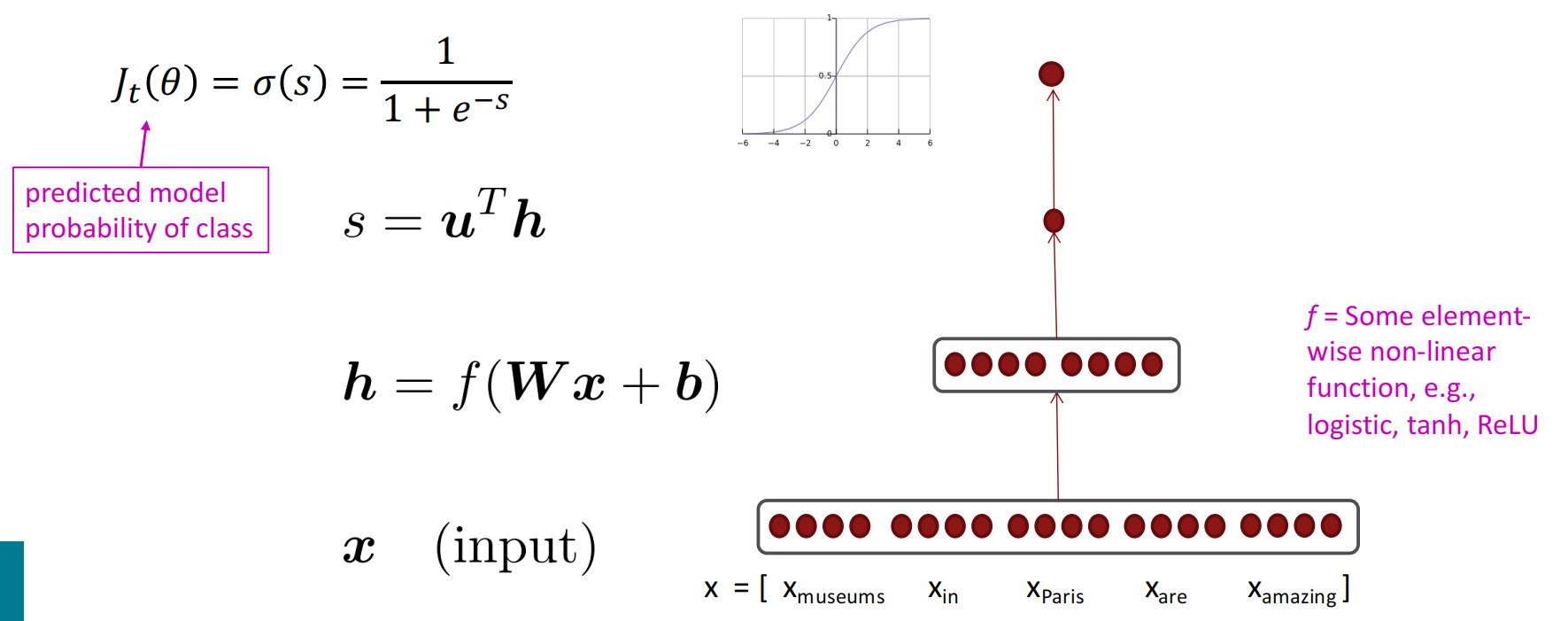
- 经过神经网络层,先线性计算后非线性映射
- 和向量$u^\top$相乘,整合特征
- 过一个softmax,表示成概率,这个概率代表中心词对应于特定label的概率。

矩阵求导
遵循惯例:导数的形状是参数的形状 (形状约定)
行向量
给定一个模型,n个输入,1个输出:$f(\pmb x)=f(x_1,x_2,…,x_n)$。
求导结果为:${ {\partial f} \over {\partial \pmb x} } = [{ {\partial f} \over {\partial x_1} },{ {\partial f} \over {\partial x_2} },…,{ {\partial f} \over {\partial x_n} }]$
矩阵
给定一个模型,n个输入,m个输出:$f(\pmb x)=[f_1(x_1,x_2,…,x_n),f_2(x_1,x_2,…,x_n),…,f_m(x_1,x_2,…,x_n)]$。
求导结果为Jacobi行列式
$$
\begin{bmatrix}
{ {\partial f_1} \over {\partial x_1} }&…&{ {\partial f_1} \over {\partial x_n} }\\
\vdots&\ddots&\vdots\\
{ {\partial f_m} \over {\partial x_1} }&…&{ {\partial f_m} \over {\partial x_n} }\\
\end{bmatrix}
$$
含向量的链式法则
给定一个模型,n个输入,n个输出:$\pmb h=f(\pmb z)$
求导结果:
$$
{ {\partial \pmb h} \over {\partial \pmb z} } =\begin{bmatrix}
f’(z_i)&0&0 \\
0 & \ddots & 0 \\
0 & 0 & f’(z_n)\\
\end{bmatrix}
$$
其中,$({ {\partial \pmb h} \over {\partial \pmb z} })_{ij} = { {\partial} \over {\partial z_j} }f(z_i) = \begin{cases} f’(z_i) \ \ \ \ i = j \\ 0\ \ \ \ otherwise \end{cases} $
其他Jacobi式求导
$$
\begin{align}
{ {\partial } \over {\partial \pmb x} }(\pmb {Wx} + \pmb b)& = \pmb W \\
{ {\partial } \over {\partial \pmb b} }(\pmb {Wx} + \pmb b)& = \pmb I \\
{ {\partial } \over {\partial \pmb u} }(\pmb u^\top\pmb h)& = \pmb h^\top \\
\end{align}
$$
反向传播的引入
在计算${ {\partial s} \over {\partial \pmb b } }$和${ {\partial s} \over {\partial \pmb W } }$时,链式法则中前面的非线性求导的部分是一样的,引入$\delta$来保存这个变量:

$\delta$被称为局部误差信号,从高层传送到低层,用于简化计算。
整体求导


根据链式法则,${ {\partial s} \over {\partial \pmb W } }=\delta $ ${ {\partial \pmb z} \over {\partial \pmb W } }$,经形状推导之后的结果为
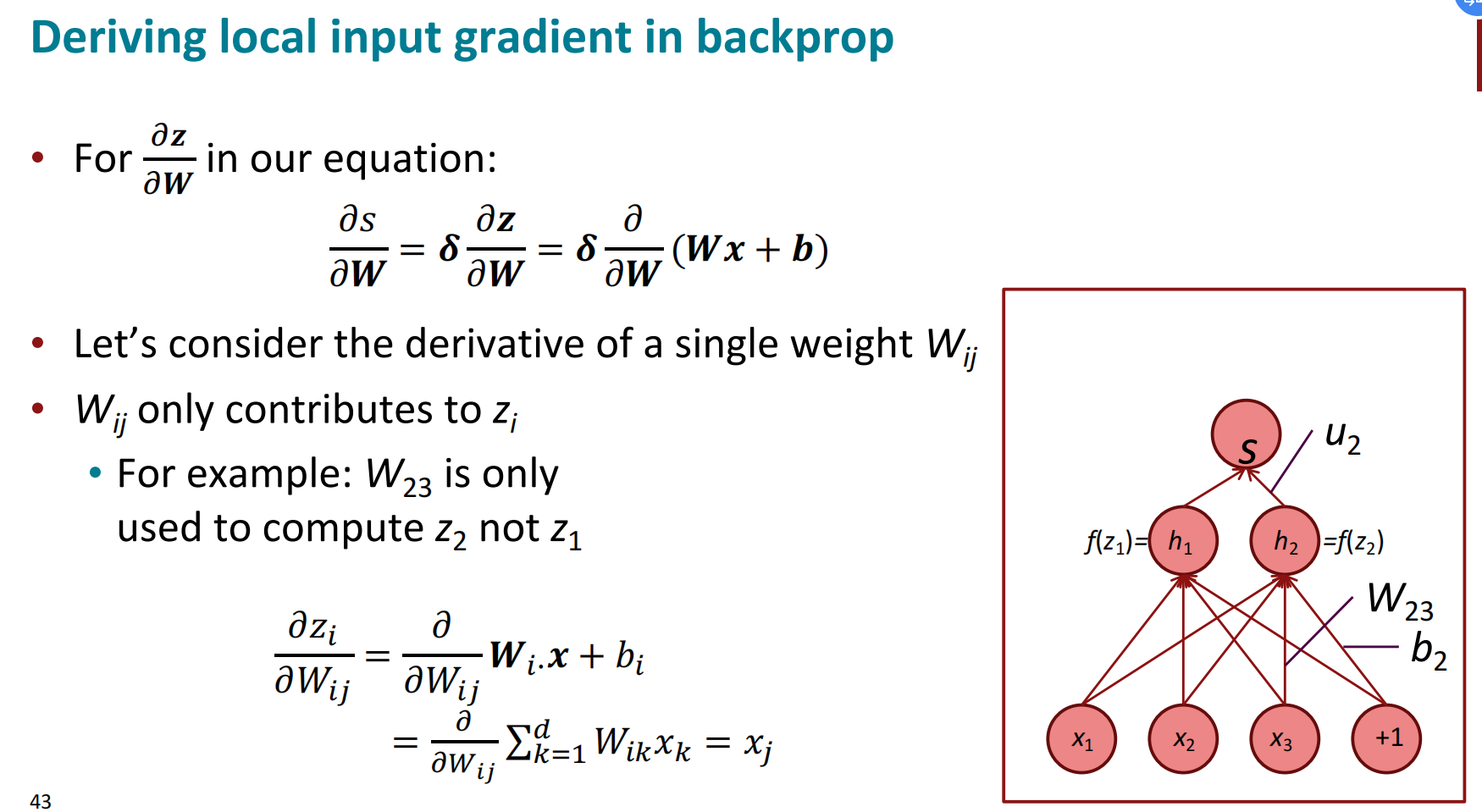

相似的,${ {\partial s} \over {\partial \pmb b } } = \pmb h^\top \circ f’(\pmb z)$的结果是一个行向量,但形状约定要求我们的梯度应该是一个列向量,因为$\pmb b$是列向量。所以,在Jacobian形式(使链式法则容易计算)和形状约定中(使优化方法SGD容易计算)是有冲突的。为了解决这个问题有两种办法:
- 先用Jacobian形式完成矩阵计算,最后重塑形状到形状约定形式(如${ {\partial s} \over {\partial \pmb b } }$)
- 始终遵循形状约定计算结果(如${ {\partial s} \over {\partial \pmb W } }$)

反向传播
计算图和反向传播
前文提到了,在相同层的参数有许多重复的计算,可以使用一个$\delta$变量简化梯度计算过程,反向传播就是这个思想的具体实现。
具体的,引入神经网络的计算图,首先对神经网络执行前向过程,计算出损失与结果;然后从最后面的节点往前回溯,反向计算各个节点的梯度。
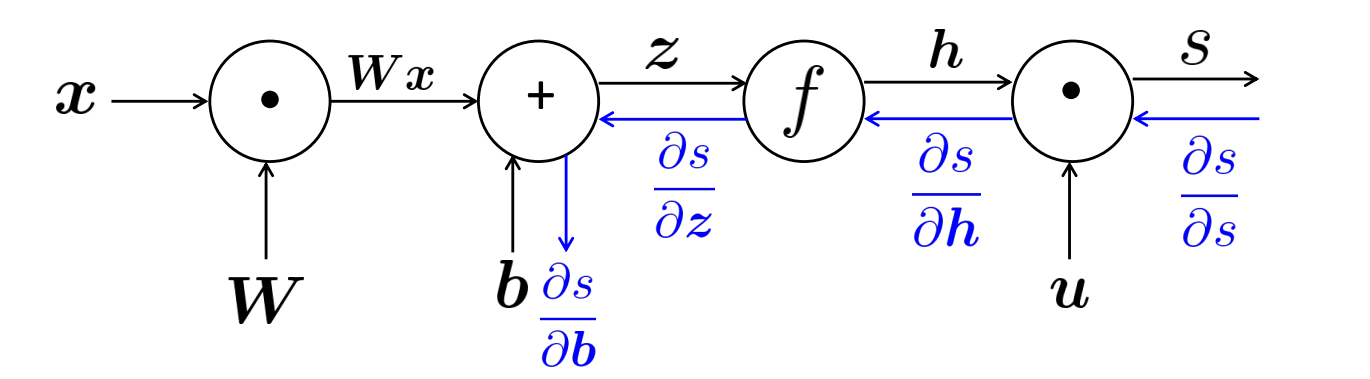
对计算图中除首节点的每个结点,都可以执行反向传播的过程,从上游传回梯度,和节点的局部梯度计算,再将结果作为下游梯度继续回传。
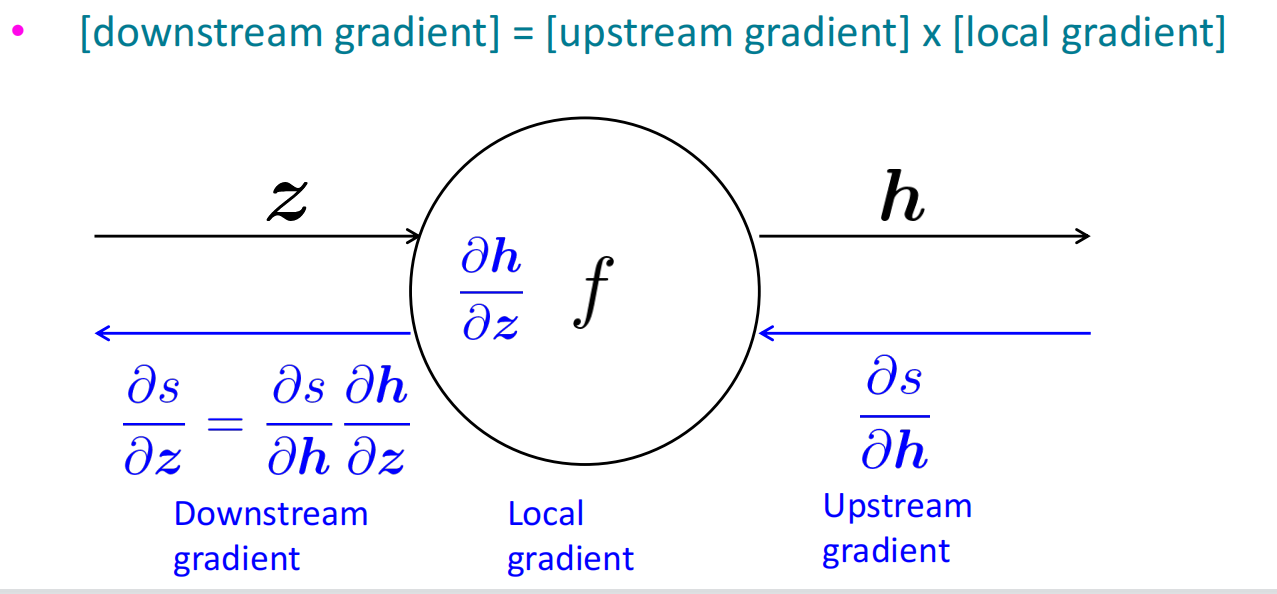
在计算图中具体是有三种类型:
单输入单输出:如上图所示
多输入单输出:对输入的每一个岔路都做一遍反向传播
单输入多输出:将多个上游的结果做加和
$$
{ {\partial f} \over {\partial y} } ={ {\partial f} \over {\partial a} }{ {\partial a} \over {\partial y} }+{ {\partial f} \over {\partial b} }{ {\partial b} \over {\partial y} }
$$
反向传播的示例如下,需要注意的是,每次计算梯度时,我们应用的应该是回传到节点的中间值,上游梯度,也称$\delta$,而不是重新从结尾计算梯度。
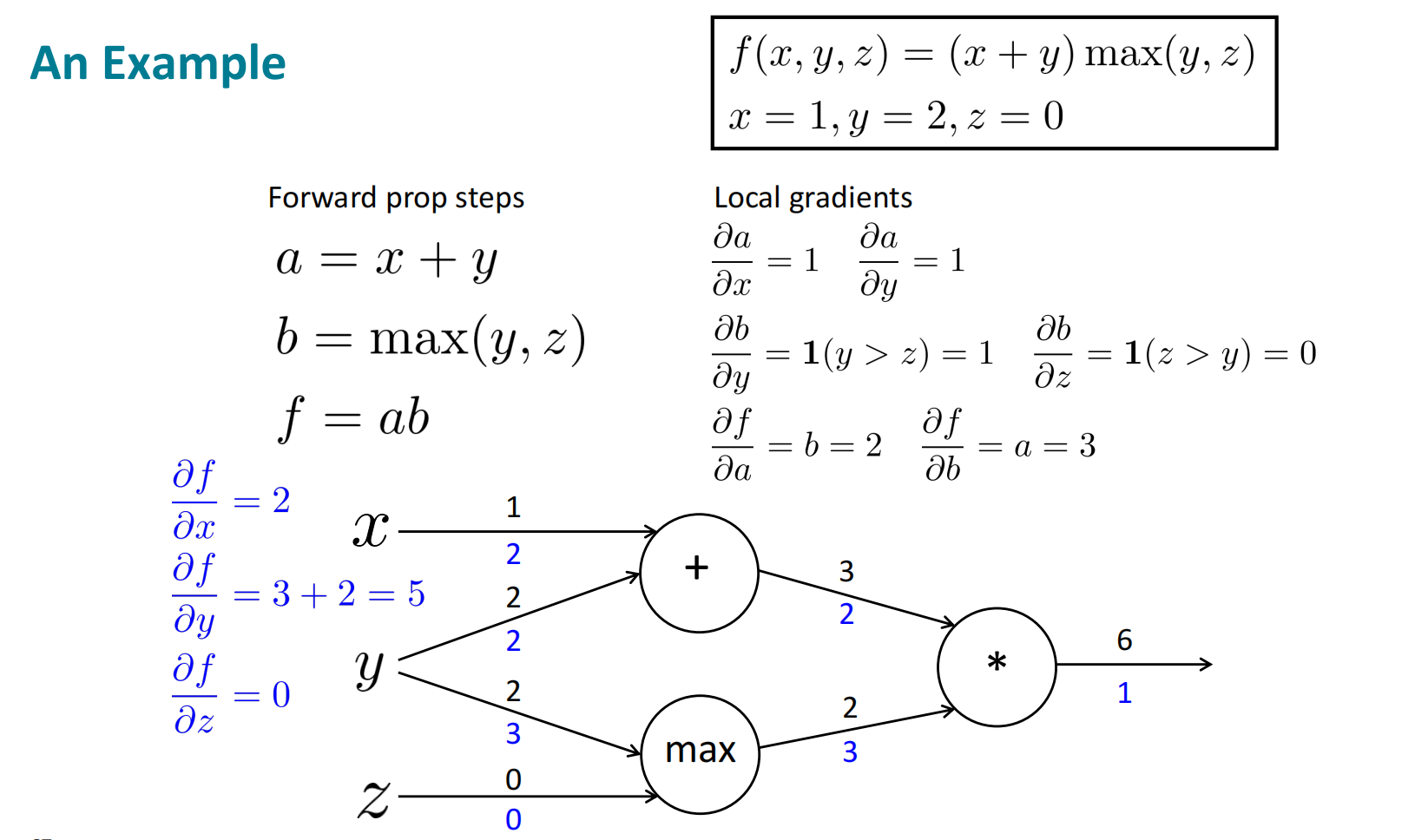
对上图计算图中的节点作直观理解:
- ‘+’ distributes the upstream gradient
- ‘max’ routes the upstream gradient
- ‘*’ switches the upstream gradient
反向传播的一般模型
反向传播的一般模型也遵循着先前向后反向的过程,需要注意的是输出分叉的加和。
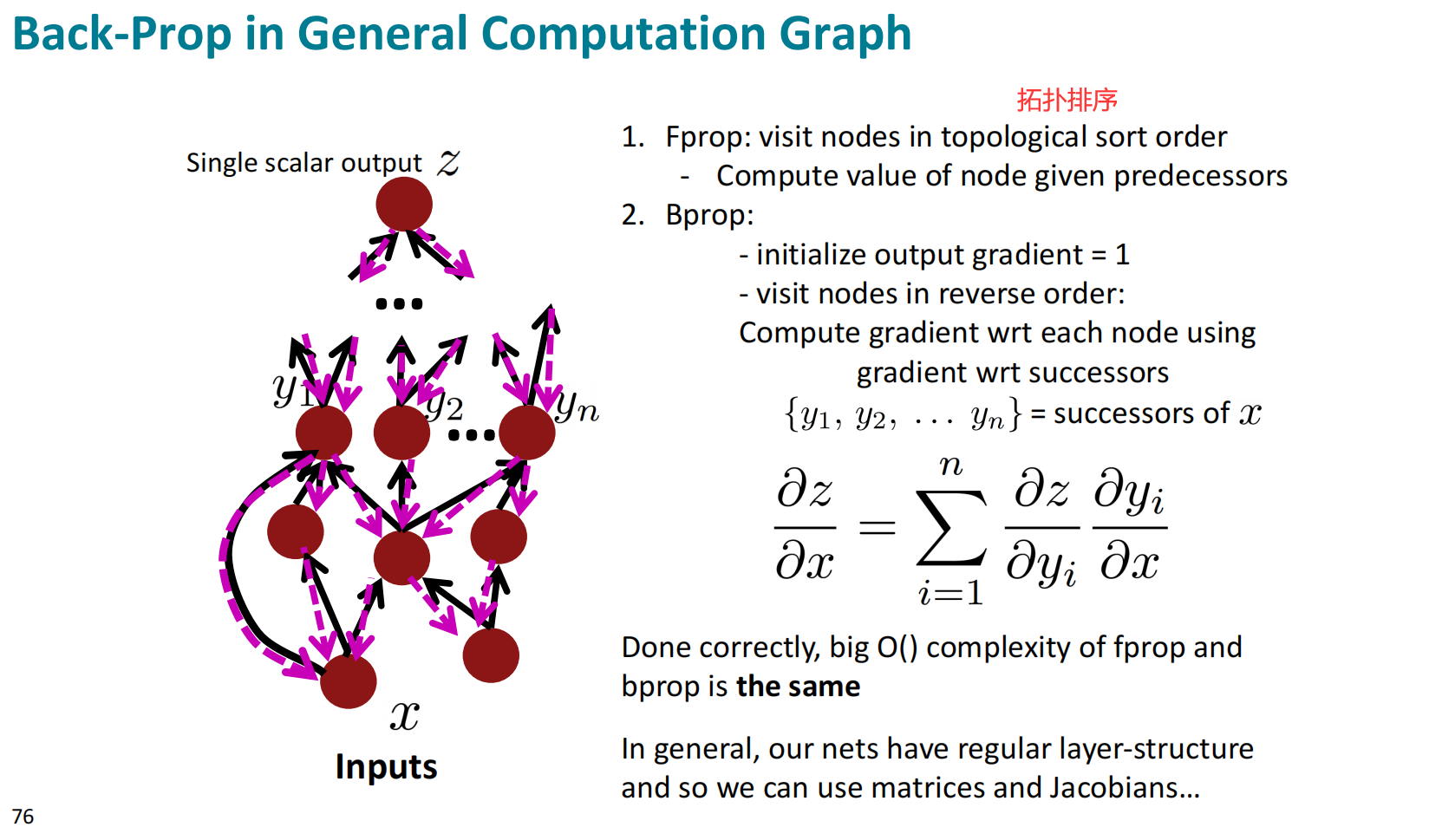
反向传播的计算过程理论上可以通过计算机自主实现,其实际也是在主流深度学习框架中已经有所应用,上述的自动计算过程被称为自动微分。
反向传播的实现
- 首先实现计算图,并定义整体逻辑(前向和反向)
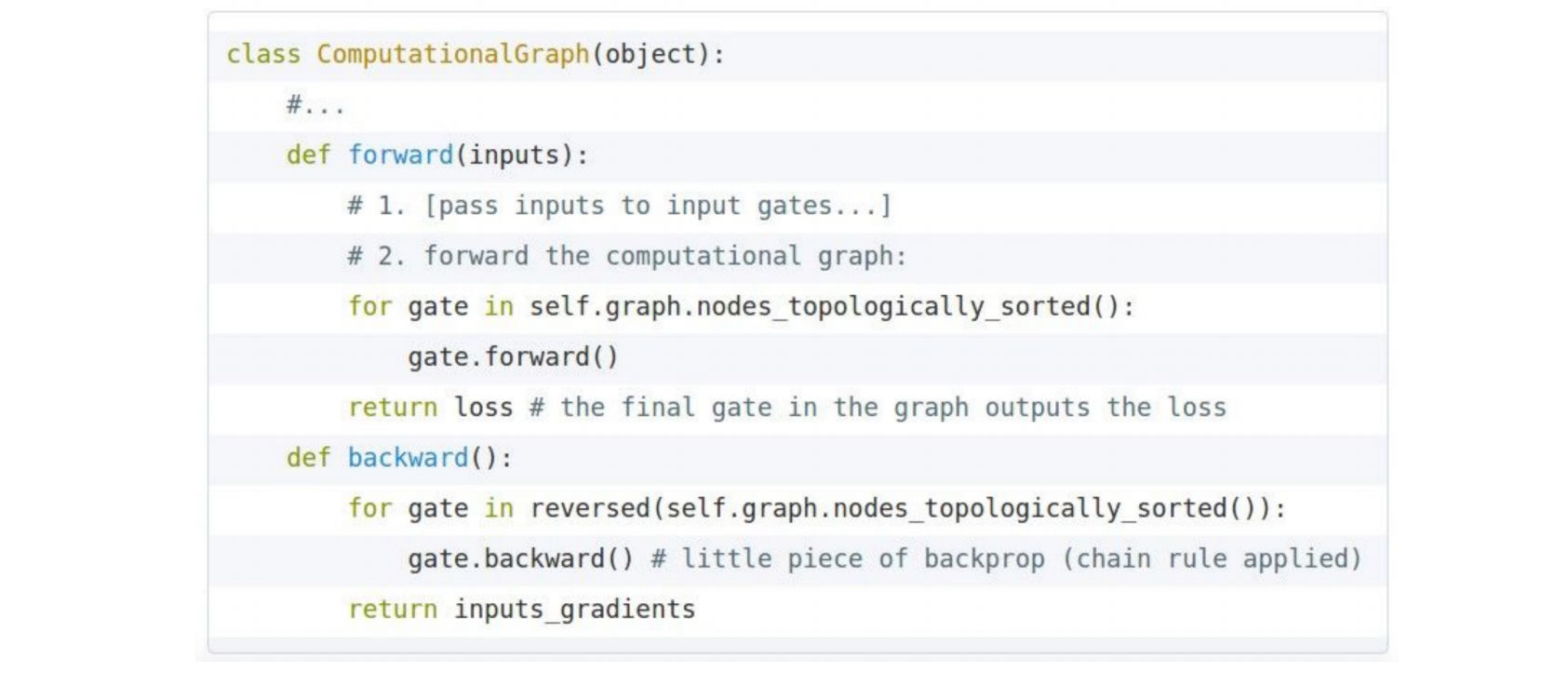
- 然后定义门控节点的前向和反向过程

梯度计算的数值检查
梯度计算的数值检查可以通过手动计算函数斜率的方式实现,这种方式的近似过程十分缓慢,需要对参数逐个作计算,但是一种十分有效的方法。

课后问题
本讲暂无