nndl编程练习3：logistic回归和softmax回归练习题解

本文最后更新于：几秒前

logistic回归

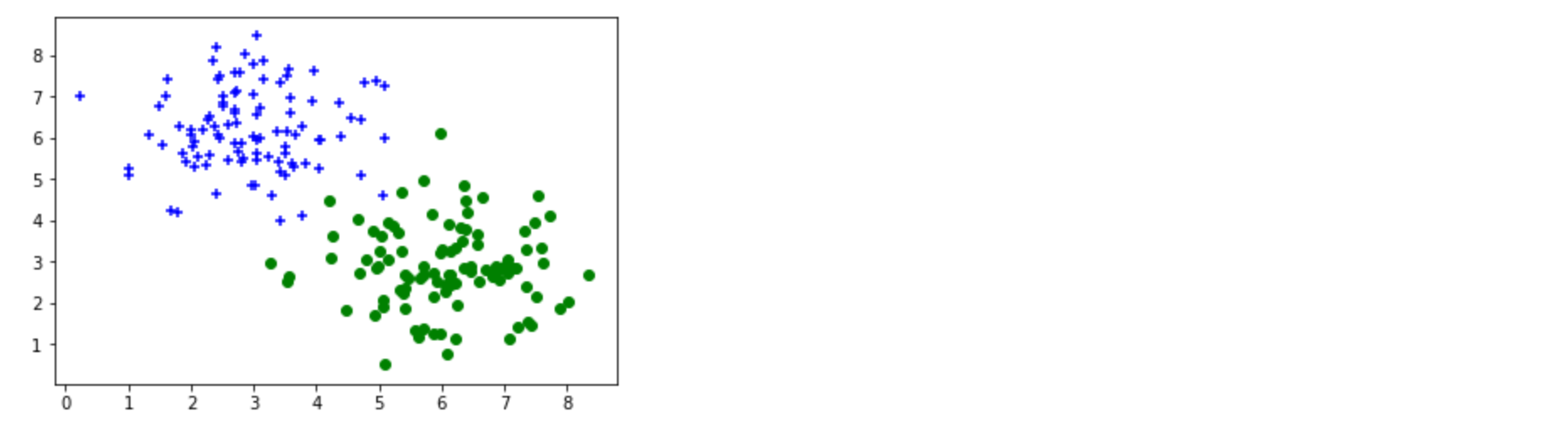
生成数据集， 看明白即可无需填写代码

‘+‘ 从高斯分布采样 (X, Y) ~ N(3, 6, 1, 1, 0).

‘o‘ 从高斯分布采样 (X, Y) ~ N(6, 3, 1, 1, 0)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import tensorflow as tf
import matplotlib.pyplot as plt

from matplotlib import animation, rc
from IPython.display import HTML
import matplotlib.cm as cm
import numpy as np
%matplotlib inline

dot_num = 100
x_p = np.random.normal(3., 1, dot_num)
y_p = np.random.normal(6., 1, dot_num)
#标签为1
y = np.ones(dot_num)
C1 = np.array([x_p, y_p, y]).T

x_n = np.random.normal(6., 1, dot_num)
y_n = np.random.normal(3., 1, dot_num)
#标签为0
y = np.zeros(dot_num)
C2 = np.array([x_n, y_n, y]).T

plt.scatter(C1[:, 0], C1[:, 1], c='b', marker='+')
plt.scatter(C2[:, 0], C2[:, 1], c='g', marker='o')

data_set = np.concatenate((C1, C2), axis=0)
np.random.shuffle(data_set)

image-20230206235625055

建立模型

建立模型类，定义loss函数，定义一步梯度下降过程函数

填空一：实现sigmoid的交叉熵损失函数(不使用tf内置的loss函数)

logistic线性模型的损失函数为交叉熵损失
$$
\mathcal L(\theta) = -{1\over N}\sum_{n=1}^N (y^{(n)} \log\hat y^{(n)}+(1-y^{(n)})\log (1-\hat y^{(n)}))
$$
在这里解代码在预测值后面加上了一个极小量$\epsilon=10^{-12}$，这个的意义我暂时还不太知晓。

这里的代码做了两个改动，分别对应于两个报错：

  1. TypeError: Input ‘b’ of ‘MatMul’ Op has type float32 that does not match type float64 of argument ‘a’.
    解决办法：在报错的行，用tf.cast作强制转型

    1
    2
    3
    4
    #原代码
    #logits = tf.matmul(inp, self.W) + self.b # shape(N, 1)
    #修改后代码
    logits = tf.matmul(tf.cast(inp,tf.float32), self.W) + self.b # shape(N, 1)

  2. TypeError: Expected float32, but got Tensor(“label:0”, shape=(), dtype=float64) of type ‘Tensor’.
    解决办法：去掉@tf.function，防止强制转换float为tensor
    见代码注释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
epsilon = 1e-12
class LogisticRegression():
    def __init__(self):
        self.W = tf.Variable(shape=[2, 1], dtype=tf.float32, 
            initial_value=tf.random.uniform(shape=[2, 1], minval=-0.1, maxval=0.1))
        self.b = tf.Variable(shape=[1], dtype=tf.float32, initial_value=tf.zeros(shape=[1]))
        
        self.trainable_variables = [self.W, self.b]
    # delete @tf.function
    def __call__(self, inp):
        # 增加tf.cast转换数据格式
        logits = tf.matmul(tf.cast(inp,tf.float32), self.W) + self.b # shape(N, 1)
        pred = tf.nn.sigmoid(logits)
        return pred
# delete @tf.function
def compute_loss(pred, label):
    if not isinstance(label, tf.Tensor):
        label = tf.constant(label, dtype=tf.float32)
    pred = tf.squeeze(pred, axis=1)
    '''============================='''
    #输入label shape(N,), pred shape(N,)
    #输出 losses shape(N,) 每一个样本一个loss
    #todo 填空一，实现sigmoid的交叉熵损失函数(不使用tf内置的loss 函数)
    '''============================='''
    #
    losses = - label*tf.math.log(pred+epsilon) - (1.-label)*tf.math.log(1.-pred+epsilon)
    loss = tf.reduce_mean(losses)
    
    pred = tf.where(pred>0.5, tf.ones_like(pred), tf.zeros_like(pred))
    accuracy = tf.reduce_mean(tf.cast(tf.equal(label, pred), dtype=tf.float32))
    return loss, accuracy
# delete @tf.function
def train_one_step(model, optimizer, x, y):
    with tf.GradientTape() as tape:
        pred = model(x)
        loss, accuracy = compute_loss(pred, y)
        
    grads = tape.gradient(loss, model.trainable_variables)
    optimizer.apply_gradients(zip(grads, model.trainable_variables))
    return loss, accuracy, model.W, model.b

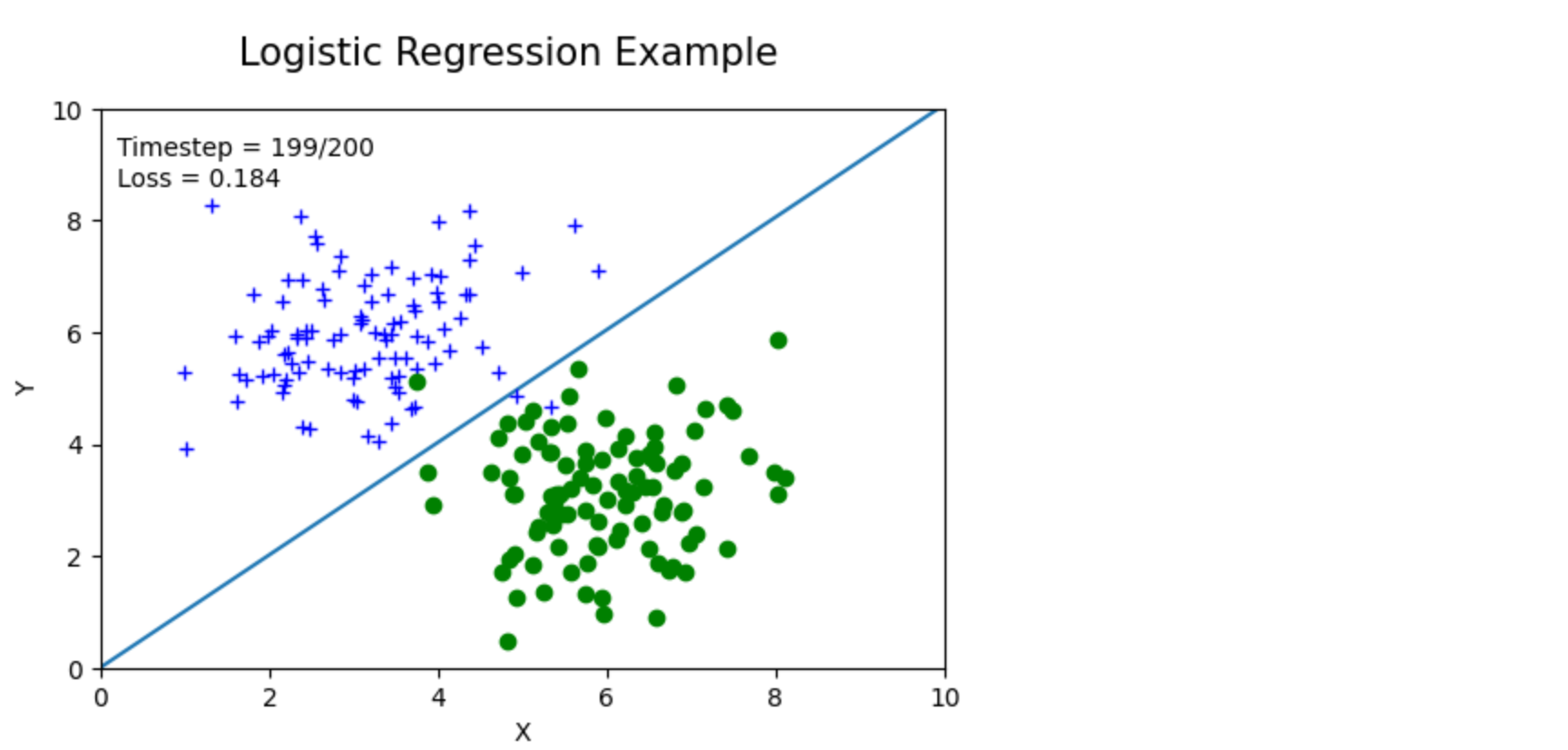
实例化一个模型，进行训练

1
2
3
4
5
6
7
8
9
10
11
12
if __name__ == '__main__':
    model = LogisticRegression()
    opt = tf.keras.optimizers.SGD(learning_rate=0.01)
    x1, x2, y = list(zip(*data_set))
    x = list(zip(x1, x2))
    animation_fram = []
    
    for i in range(200):
        loss, accuracy, W_opt, b_opt = train_one_step(model, opt, x, y)
        animation_fram.append((W_opt.numpy()[0, 0], W_opt.numpy()[1, 0], b_opt.numpy(), loss.numpy()))
        if i%20 == 0:
            print(f'loss: {loss.numpy():.4}\t accuracy: {accuracy.numpy():.4}')

image-20230207010103726

结果展示，无需填写代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
f, ax = plt.subplots(figsize=(6,4))
f.suptitle('Logistic Regression Example', fontsize=15)
plt.ylabel('Y')
plt.xlabel('X')
ax.set_xlim(0, 10)
ax.set_ylim(0, 10)

line_d, = ax.plot([], [], label='fit_line')
C1_dots, = ax.plot([], [], '+', c='b', label='actual_dots')
C2_dots, = ax.plot([], [], 'o', c='g' ,label='actual_dots')


frame_text = ax.text(0.02, 0.95,'',horizontalalignment='left',verticalalignment='top', transform=ax.transAxes)
# ax.legend()

def init():
    line_d.set_data([],[])
    C1_dots.set_data([],[])
    C2_dots.set_data([],[])
    return (line_d,) + (C1_dots,) + (C2_dots,)

def animate(i):
    xx = np.arange(10, step=0.1)
    a = animation_fram[i][0]
    b = animation_fram[i][1]
    c = animation_fram[i][2]
    yy = a/-b * xx +c/-b
    line_d.set_data(xx, yy)
        
    C1_dots.set_data(C1[:, 0], C1[:, 1])
    C2_dots.set_data(C2[:, 0], C2[:, 1])
    
    frame_text.set_text('Timestep = %.1d/%.1d\nLoss = %.3f' % (i, len(animation_fram), animation_fram[i][3]))
    
    return (line_d,) + (C1_dots,) + (C2_dots,)
#FuncAnimation函数绘制动图，f是画布，animate是自定义动画函数，init_func自定义开始帧，即传入init初始化函数，
#frames动画长度，一次循环包含的帧数，在函数运行时，其值会传递给函数animate(i)的形参“i”，interval更新频率，以ms计，blit选择更新所有点，还是仅更新产生变化的点。
anim = animation.FuncAnimation(f, animate, init_func=init,
                               frames=len(animation_fram), interval=30, blit=True)

HTML(anim.to_html5_video())

image-20230207010259507

Softmax回归

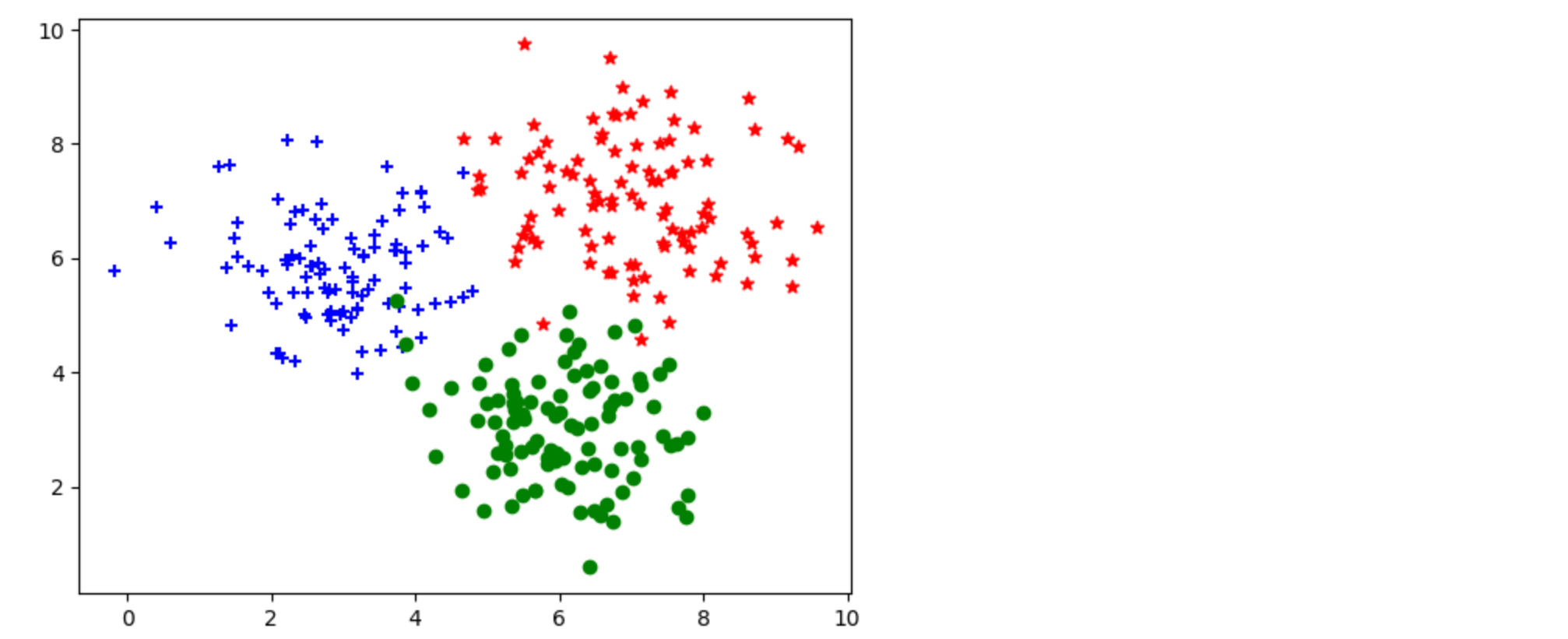
生成数据集， 看明白即可无需填写代码

‘+‘ 从高斯分布采样 (X, Y) ~ N(3, 6, 1, 1, 0).

‘o‘ 从高斯分布采样 (X, Y) ~ N(6, 3, 1, 1, 0)

‘*‘ 从高斯分布采样 (X, Y) ~ N(7, 7, 1, 1, 0)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import tensorflow as tf
import matplotlib.pyplot as plt

from matplotlib import animation, rc
from IPython.display import HTML
import matplotlib.cm as cm
import numpy as np
%matplotlib inline

dot_num = 100
x_p = np.random.normal(3., 1, dot_num)
y_p = np.random.normal(6., 1, dot_num)
#标签为1
y = np.ones(dot_num)
C1 = np.array([x_p, y_p, y]).T

x_n = np.random.normal(6., 1, dot_num)
y_n = np.random.normal(3., 1, dot_num)
#标签为0
y = np.zeros(dot_num)
C2 = np.array([x_n, y_n, y]).T

x_b = np.random.normal(7., 1, dot_num)
y_b = np.random.normal(7., 1, dot_num)
#标签为2
y = np.ones(dot_num)*2
C3 = np.array([x_b, y_b, y]).T
#画出来
plt.scatter(C1[:, 0], C1[:, 1], c='b', marker='+')
plt.scatter(C2[:, 0], C2[:, 1], c='g', marker='o')
plt.scatter(C3[:, 0], C3[:, 1], c='r', marker='*')

data_set = np.concatenate((C1, C2, C3), axis=0)
np.random.shuffle(data_set)
print(data_set)

image-20230207012314335

建立模型

建立模型类，定义loss函数，定义一步梯度下降过程函数

填空一：在__init__构造函数中建立模型所需的参数

填空二：实现softmax的交叉熵损失函数(不使用tf内置的loss函数)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
epsilon = 1e-12
class SoftmaxRegression():
    def __init__(self):
        '''============================='''
        #todo 填空一，构建模型所需的参数 self.W, self.b 可以参考logistic-regression-exercise
        '''============================='''
        self.W = tf.Variable(shape=[2, 3], dtype=tf.float32, 
            initial_value=tf.random.uniform(shape=[2, 3], minval=-0.1, maxval=0.1))
        self.b = tf.Variable(shape=[1, 3], dtype=tf.float32, initial_value=tf.zeros(shape=[1, 3]))
        self.trainable_variables = [self.W, self.b]
    def __call__(self, inp):
        logits = tf.matmul(tf.cast(inp,tf.float32), self.W) + self.b # shape(N, 3)
        pred = tf.nn.softmax(logits)
        return pred    
    
def compute_loss(pred, label):
    label = tf.one_hot(tf.cast(label, dtype=tf.int32), dtype=tf.float32, depth=3)
    '''============================='''
    #输入label shape(N, 3), pred shape(N, 3)
    #输出 losses shape(N,) 每一个样本一个loss
    #todo 填空二，实现softmax的交叉熵损失函数(不使用tf内置的loss 函数)
    '''============================='''
    #对三个标签的损失求平均
    losses = - tf.reduce_mean(label * tf.math.log(pred+epsilon))
    #求总平均
    loss = tf.reduce_mean(losses) 
    
    accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(label,axis=1), tf.argmax(pred, axis=1)), dtype=tf.float32))
    return loss, accuracy
    
def train_one_step(model, optimizer, x, y):
    with tf.GradientTape() as tape:
        pred = model(x)
        loss, accuracy = compute_loss(pred, y)
        
    grads = tape.gradient(loss, model.trainable_variables)
    optimizer.apply_gradients(zip(grads, model.trainable_variables))
    return loss, accuracy

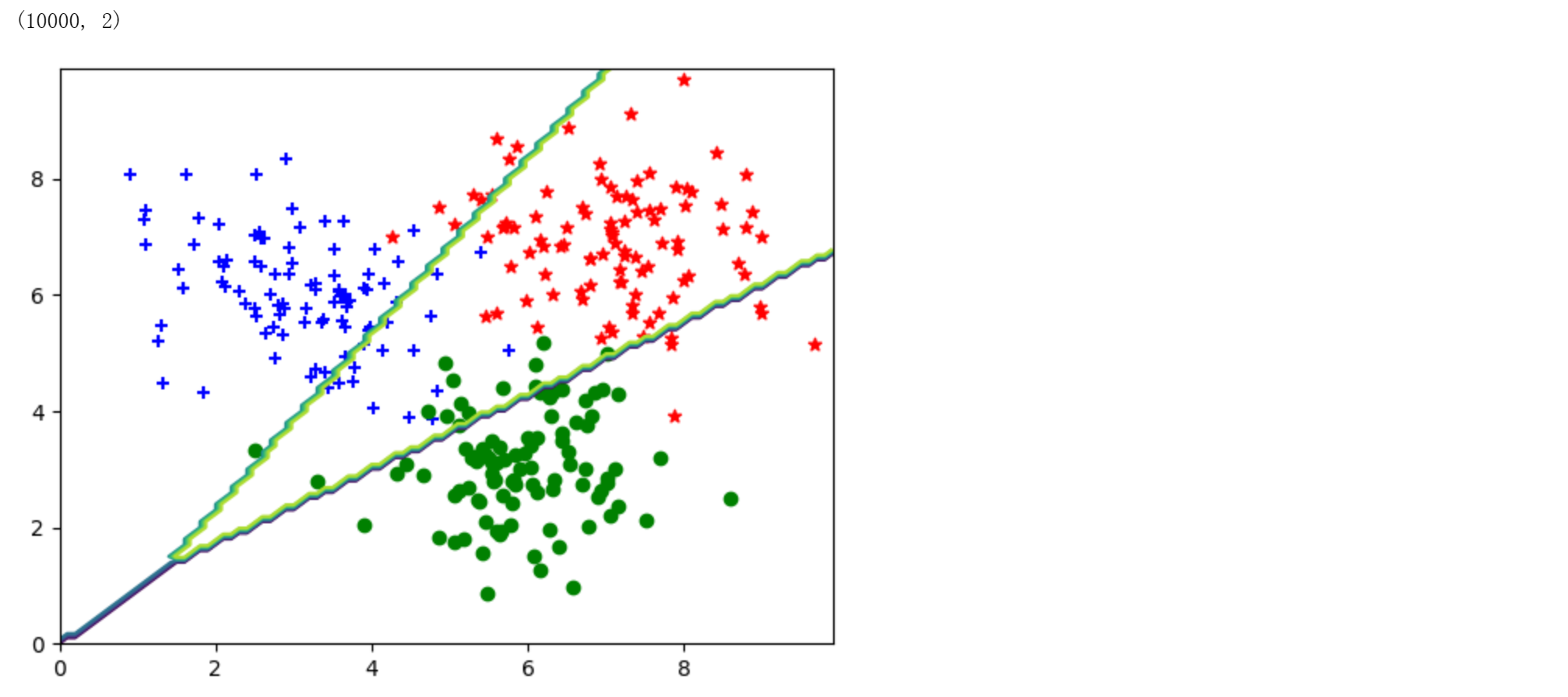
实例化一个模型，进行训练

1
2
3
4
5
6
7
8
model = SoftmaxRegression()
opt = tf.keras.optimizers.SGD(learning_rate=0.01)
x1, x2, y = list(zip(*data_set))
x = list(zip(x1, x2))
for i in range(1000):
    loss, accuracy = train_one_step(model, opt, x, y)
    if i%50==49:
        print(f'loss: {loss.numpy():.4}\t accuracy: {accuracy.numpy():.4}')

结果展示，无需填写代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
plt.scatter(C1[:, 0], C1[:, 1], c='b', marker='+')
plt.scatter(C2[:, 0], C2[:, 1], c='g', marker='o')
plt.scatter(C3[:, 0], C3[:, 1], c='r', marker='*')

x = np.arange(0., 10., 0.1)
y = np.arange(0., 10., 0.1)

X, Y = np.meshgrid(x, y)
inp = np.array(list(zip(X.reshape(-1), Y.reshape(-1))), dtype=np.float32)
print(inp.shape)
Z = model(inp)
Z = np.argmax(Z, axis=1)
Z = Z.reshape(X.shape)
plt.contour(X,Y,Z)
plt.show()

image-20230207012520185

附：对logistic回归的复现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
import tensorflow as tf
import matplotlib.pyplot as plt

from matplotlib import animation, rc
from IPython.display import HTML
import matplotlib.cm as cm
import numpy as np

dot_num = 100
x_p = np.random.normal(3., 1, dot_num)
y_p = np.random.normal(6., 1, dot_num)
y = np.ones(dot_num)
C1 = np.array([x_p, y_p, y]).T

x_n = np.random.normal(6., 1, dot_num)
y_n = np.random.normal(3., 1, dot_num)
y = np.zeros(dot_num)
C2 = np.array([x_n, y_n, y]).T

plt.scatter(C1[:, 0], C1[:, 1], c='b', marker='+')
plt.scatter(C2[:, 0], C2[:, 1], c='g', marker='o')

data_set = np.concatenate((C1, C2), axis=0)
np.random.shuffle(data_set)

#logistic模型包括模型，损失函数，迭代函数三个部分
epsilon = 1e-12
class LogisticRegression():
    def __init__(self):
        #tf.Variable：定义tf中的变量.
        #tf.random.uniform：从均匀分布中输出随机值.
        self.W = tf.Variable(shape=[2,1],dtype='float32',initial_value=tf.random.uniform(shape=[2,1],maxval=0.1,minval=-0.1))
        self.b = tf.Variable(shape=[1],dtype='float32',initial_value=tf.random.uniform(shape=[1],maxval=0.1,minval=-0.1))
        #自动求导的关键步骤
        self.trainable_variables = [self.W,self.b]
    def __call__(self,inp):
        logits = tf.matmul(tf.cast(inp,tf.float32),self.W)+self.b
        pred = tf.nn.sigmoid(logits)
        return pred

def compute_loss(pred,label):
    if not isinstance(label, tf.Tensor):
        label = tf.constant(label, dtype=tf.float32)
    #tf.squeeze：去掉维度为1的维度
    pred = tf.squeeze(pred,axis=1)
    losses = -label*tf.math.log(pred+epsilon)-(1.-label)*tf.math.log(1.-pred+epsilon)
    loss = tf.reduce_mean(losses)
    #tf.where：确定表达式为真的位置
    pred = tf.where(pred>0.5,tf.ones_like(pred),tf.zeros_like(pred))
    accuracy = tf.reduce_mean(tf.cast(tf.equal(pred,label),dtype='float32'))
    return loss,accuracy

def train_one_step(model,optimizer,x,y):
    # tf自动求导API
    with tf.GradientTape() as tape:
        pred = model(x)
        loss,accuracy = compute_loss(pred,y)
    #自动求导
    #先求导
    gradient = tape.gradient(loss,model.trainable_variables)
    #后优化
    optimizer.apply_gradients(zip(gradient,model.trainable_variables))
    return loss,accuracy,model.W,model.b

if __name__ == "__main__":
    alpha = 0.01
    epoch = 200
    model = LogisticRegression()
    opt = tf.keras.optimizers.SGD(learning_rate=alpha)
    #zip(*data_set)相当于解压操作，(x1,x2,y)中的每一维都提取出来
    x1,x2,y = list(zip(*data_set))
    x = list(zip(x1,x2))
    animation_fram = []
    for i in range(epoch):
        loss,accuracy,W,b = train_one_step(model,opt,x,y)
        animation_fram.append((W.numpy()[0, 0], W.numpy()[1, 0], b.numpy(), loss.numpy()))
        if i % 20 == 0:
            print(f'loss: {loss.numpy():.4}\t accuracy: {accuracy.numpy():.4}')
学习笔记
#神经网络与深度学习 #python
nndl编程练习3：logistic回归和softmax回归练习题解
http://paopao0226.site/post/58d83785.html
作者
Ywj226
发布于
2023年2月6日
更新于
2023年9月23日
许可协议