CS224N课程P1：简介和词向量

课程词汇

controversial - 矛盾的；有争议的
manipulate - 操作；使用
pithy - 精辟的；准确的
truncate - 截断
scalable - 可扩展的

课程内容

导引

1、什么是指称语义

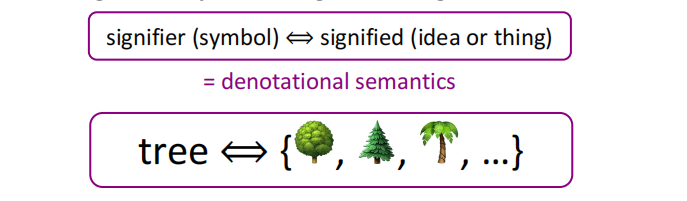
是通过构造表达其语义的（叫做指称 (denotation)或意义的）数学对象来形式化计算机系统的语义的一种方法。即：实现语义和符号的对应关系。

2、局部表示和分布式表示

局部表示是用离散变量存储单词信息，这种符号化表示可以用one-hot编码表示

缺点：由于单词向量正交，无法体现单词间的相关性

分布式表示的重点在于用上下文信息（固定窗口）表示原单词（A word’s meaning is given by the words that frequently appear close-by）

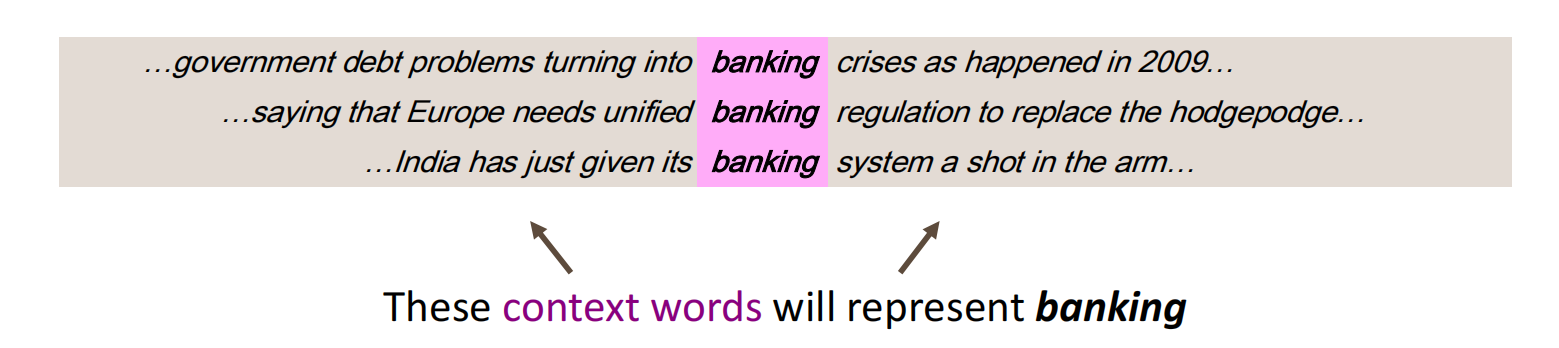
在分布式表示下，单词作为标记分布在高维空间中，距离（在这里可以指欧氏距离）相近的标记其语义也相似。

3、类型和标记（Type & Token）

token（标记）：文本内出现的单词总数叫做文本标记数

type（类型）：文本内出现的不同的单词总数叫做文本类型数

例子：She is directly astonished by the astonishing thing, and directly stared at him in astonishment.

句子一共出现了15个单词，故此句有15个token；句子中不同单词有14个（directly出现两次），故此句有14个type。

分布式词向量：Word2Vec

概述（Overview）

思想（Idea）

• We have a large corpus (“body”) of text: a long list of words
• Every word in a fixed vocabulary is represented by a vector
• Go through each position t in the text, which has a center word（中心词） c and context (“outside”) words （上下文词）o
• Use the similarity of the word vectors for c and o to calculate the probability of o given c (or vice versa)
• Keep adjusting the word vectors to maximize this probability

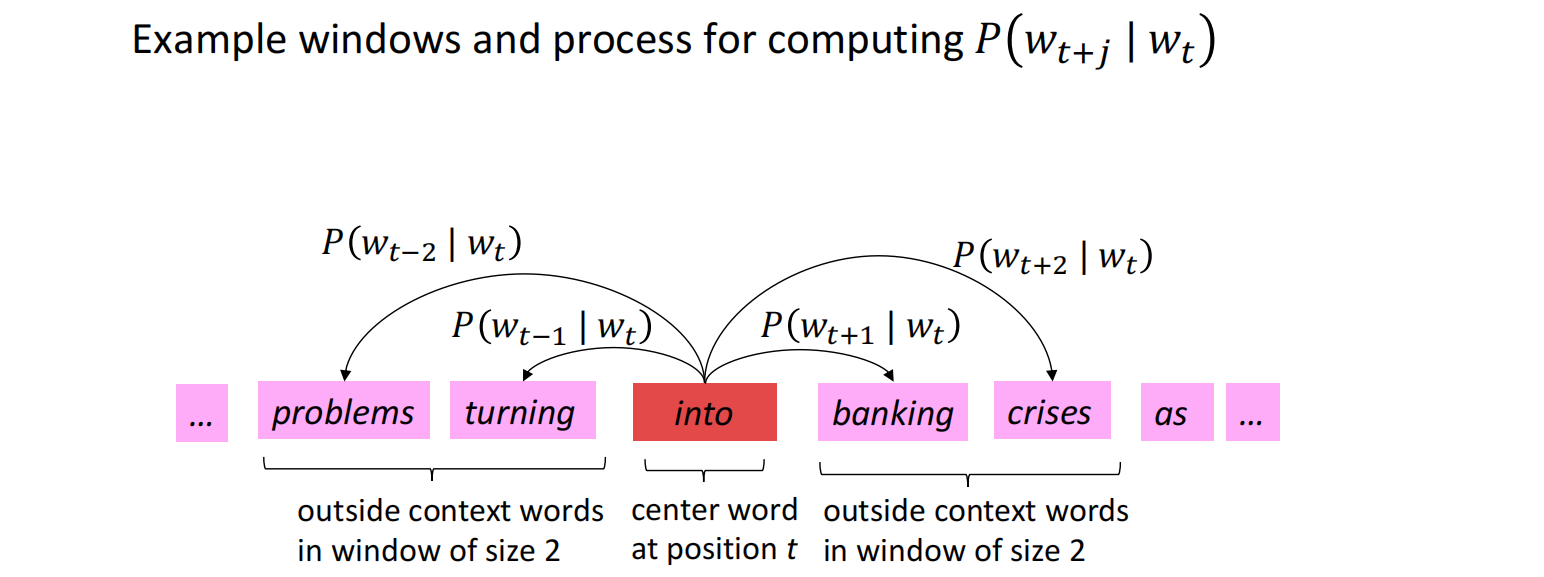
模型（Model）

目标函数（Objective Function）

对于每个位置$t\in[1,T],t\in Z$，给定单词$w_t$，预测在窗口为固定值$m$的范围内的上下文，其数值似然为

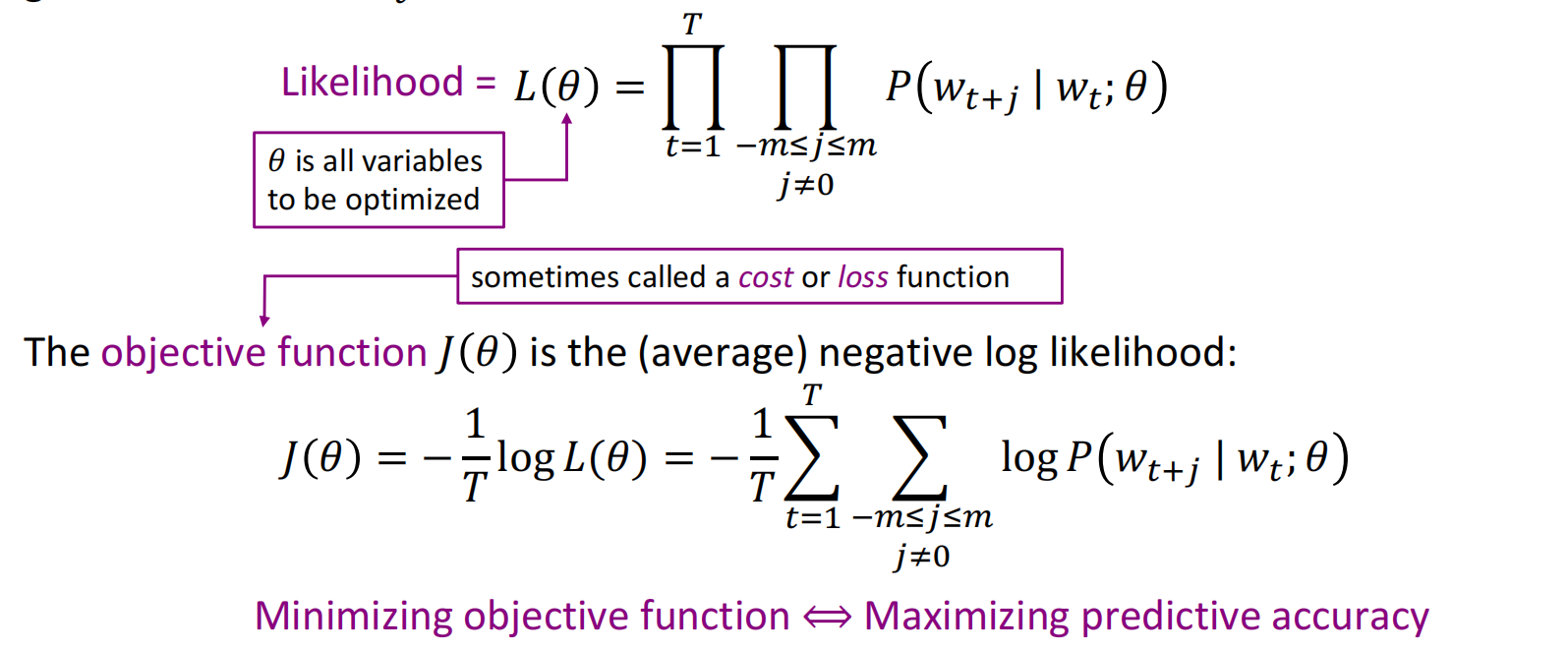
其中，对数似然可以使计算从乘法变成加法，简化计算难度；除以$T(词汇总量)$用于归一化；负号将最大化问题转化为最小化问题。后面两个处理是计算习惯使然。

预测函数（Predict Function）

似然$p(w_{t+j}|w_t;\theta)$的计算需要引入两个词向量：$v_w$和$u_w$：

• $v_w$：$w$作为中心词时的词向量
• $u_w$：$w$作为上下文词时的词向量

然后引入似然概率计算公式，其中$V$是上下文词汇集合。
$$
P(o|c)={ {\exp(u_o^\top v_c)} \over {\sum_{w\in v}\exp(u_w^\top v_c)} }
$$
对于此公式，解释是这样的：

需要强调的是，点积的处理中是有相似性的度量因素在的。

梯度计算

目标函数
$$
J(\theta) = -{1\over T} \sum_{t=1}^T \sum_{-m \le j \le m,j\ne 0} \log P(w_{t+j}|w_t;\theta) \tag{1}
$$
优化函数
$$
P(o|c)={ {\exp(u_o^\top v_c)} \over {\sum_{w\in V}\exp(u_w^\top v_c)} } \tag{2}
$$
目标函数对中心词$v_c$求偏导，注意这里用到了向量求导的基本知识
$$
\begin{align}
{ \partial \over {\partial v_c} } \log { {\exp(u_o^\top v_c)} \over {\sum_{w\in V}\exp(u_w^\top v_c)} } & = ①-② \\
① & = { \partial \over {\partial v_c} } \log {\exp(u_o^\top v_c) } = { \partial \over {\partial v_c} } u_o^\top v_c = u_o(向量导数)\\
② & = { \partial \over {\partial v_c} } \log { \sum_{w\in V} \exp(u_w^\top v_c) } = { 1 \over { \sum_{w\in V} \exp(u_w^\top v_c) } } \sum_{x\in V} \exp(u_x^\top v_c) · u_x(变换参数) \\
∴{ \partial \over {\partial v_c} } \log P(o|c) & = u_o - { {\sum_{x\in V} \exp(u_x^\top v_c) u_x} \over {\sum_{w\in V} \exp (u_w^\top v_c)} } \\
& = u_o - \sum_{x\in V} { {\exp(u_x^\top v_c) } \over {\sum_{w\in V} \exp (u_w^\top v_c)} }u_x (softmax形式) \\
& = u_o - \sum_{x\in V}P(x|c)u_x \\
& = observed - expected
\end{align}
$$
其中$u_o$可以看作观测结果，$\sum_{x\in V}P(x|c)u_x$是对上下文概率的平均，是期望值，$softmax$形式的式子，其开导数的结果很多都是表达为观测值和期望值的接近程度。

课后问题

Q：中心词向量和上下文词向量如何能用一个向量表示？

A：不同人使用不同的结合方法，最典型的是取平均，因为这两个向量再训练之后会十分相似。

Q：一个词可能有多种意思，如何表示？

A：或许有一点奇怪，但将多个意思用一个词向量表示，其效果还不错。

Q：可以学到Alexa的部分吗？

A：你应该学CS224S。

Q：对立面的平衡是如何做的呢？（如电影很差/电影很好）

A：词向量模型对对立面的关注做的很差，现在还没有实现捕获。

Q：词向量在虚词（so/not,etc.）的效果好吗

A：很多情况下他们区别不太大，但我们确实也建立了这些词的词向量，word2vec对这些词的敏感度不强，之后会有对句子结构捕捉效果更好的模型。

Q：对Word2Vec的优化

A：商业应用比如有Skip Grand、负采样等。