CS224N课程P7:注意力机制与Transformer
本文最后更新于:几秒前
课程词汇
1 | |
课程内容
Decoding的优化
Greedy decoding
在Seq2seq的Decoder中,Decoder的每一步生成目标语句的单词时,都是从Decoder隐状态给出的分布中选择一个概率最大的,即求argmax,这种不断通过argmax的结果作为下一步Decoder输入的过程我们称之为Greedy decoding,即每次都选最好的,这体现了一种贪心的思想。
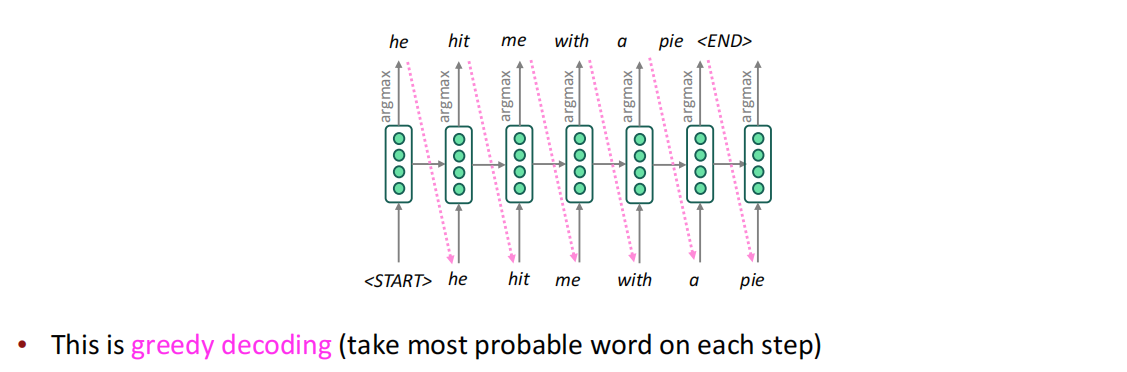
Greedy Decoder有一个比较大的缺陷,在于其每次选择之后就不能回退并修改,如果模型在其中一步预测有误时,其会一直影响之后目标语句的结果和网络的输出。为了解决这种问题,可以采取迭代的方式,将各种可能性都考虑到,然后选出其中的最优。理论上,在机器翻译中的decoder的目标为:

在每一步t,我们可以查看词汇表$V^t$中的所有可能的翻译,然后选择最优。这种方法能够解决Greedy decoding的错误影响,但每次的工作量巨大,其时间复杂度$O(V^t)$也不好。为此引入Beam search decoding
Beam search decoding
Beam search decoding的主要作用在于降低查找规模,在decoding的每一步t,保留k个最有可能的部分翻译(称之为假设),k被称之为beam size(一般在5-10)。
设一个假设为$y_1,…,y_t$,这个假设会有一个分数,这个分数就是它的对数概率:
$$
{\rm score}(y_1,…,y_t) = \log P_{LM}(y_1,…,y_t|x) = \sum_{i=1}^t \log P_{LM}(y_i|y_1,…,y_{i-1},x)
$$
分数都是负数,且分数越高其表现越好。Beam search不保证每次能够找到最优解,但其处理效率会远远好于全查找(Exhausted search)。
Beam search的流程如下。每次搜索节点先计算当前位置的$\log P_{LM}$,然后取到上游结果并相加,找到最优的k个假设;然后在同一层级的$k^2$个假设中找到分数最高的$k$个作为下一步搜索的根节点,一直做到结束

在beam search中,我们依旧以生成<end>作为结束符,而不同假设结束的步可能不同;通常,当我们达到了预定义的截断步$T$,或生成了预定义的$n$个假设时,搜索结束,然后计算每个假设的分数并取前k个。这里会存在一个问题:越长的假设其分数可能越低(经验),因此计算分数时需要长度归一化:
$$
{\rm score}(y_1,…,y_t) = {1 \over t} \sum_{i=1}^t \log P_{LM}(y_i|y_1,…,y_{i-1},x)
$$
Attention(注意力机制)
Seq2seq是由encoder和decoder两部分组成,其中encoder作为decoder的conditioner,提供源语句的信息;然而在提供信息时,既有的方法主要是将encoder的结果作为decoder的初始隐状态,这在信息的表达能力上有瓶颈(Bottleneck)。因此引入注意力机制解决瓶颈问题。
注意力机制的核心思想是:在decoder的每一步,decoder的隐状态都能够与encoder建立直接连接,关注于源语句的特定部分。
注意力机制的过程如图所示:
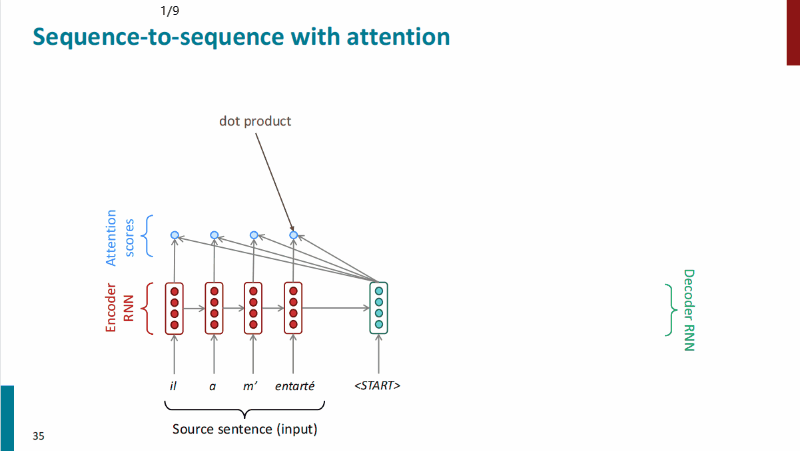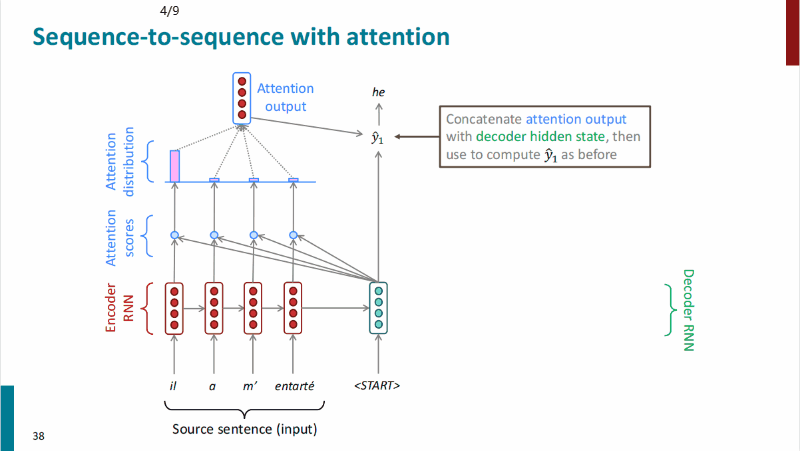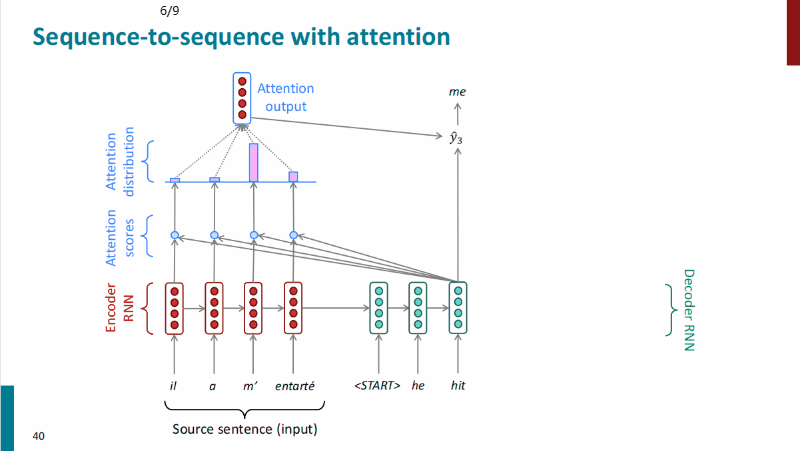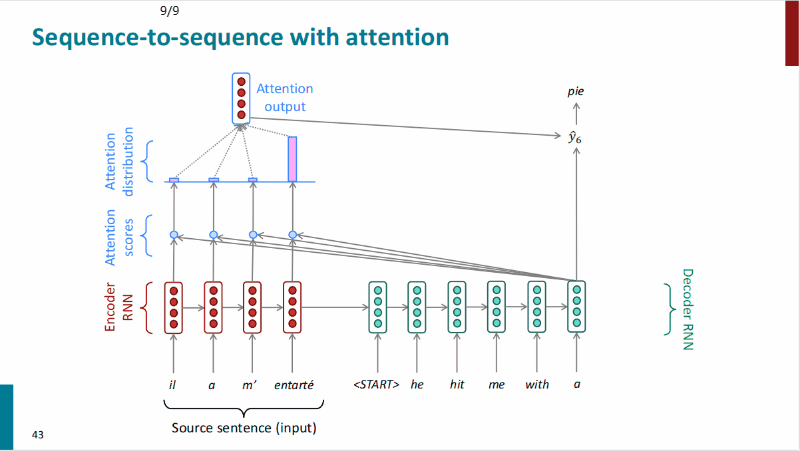
注意力机制的过程如下:
有Encoder的隐状态$h_1,…,h_N\in \mathbb R^h$和每一步t的decoder的隐状态$s_t\in \mathbb R^h$
首先获得Encoder在第t步的注意力分数$\pmb e^t$
$$
\pmb e^t = [\pmb s_t^\top \pmb h^1+…+\pmb s_t^\top \pmb h^N] \in \mathbb R^N
$$然后过一个softmax形成注意力分布$\alpha^t$
$$
\alpha^t = {\rm softmax}(\pmb e^t)\in \mathbb R^N
$$用注意力分布$\alpha^t$计算encoder隐状态的加权和作为注意力输出$\pmb a_t$
$$
\pmb a_t = \sum_{i=1}^N \alpha_ i^t\pmb h_i \in \mathbb R^h
$$最后将注意力分布$\pmb a_t$和decoder隐状态$s_t$连接起来,按照非注意力seq2seq模型继续下游工作。
$$
[\pmb a_t;\pmb s_t] \in \mathbb R^{2h}
$$
注意力机制的使用成功解决了decoder对源语句的关注,除此之外,attention还有以下的优点:
- 改进了NMT的性能,允许decoder关注源语句的特定部分;
- 提供了一种类似人类的模型回顾机制,可以回看源语句的信息而不用全盘记忆;
- 解决了seq2seq等双网络模型的bottleneck问题,允许decoder直接连接encoder;
- 缓解了梯度消失问题,decoder的直连边传递梯度;
- 提供了一部分的模型可解释性,通过注意力分布可以了解到decoder的关注信息,从而了解NMT的对齐是怎样工作的。
Attention的共性流程
Attention虽然有各种变种,但其主要流程是基本不变的,给定查询的值$\pmb h_1,…,\pmb h_N\in \mathbb R^{d_1}$和一个查询$\pmb s\in \mathbb R^{d_2}$,Attention的基本流程大致为:
- 计算注意力分数$\pmb e \in \mathbb R^N$;
- 使用softmax等将分数转成分布$\alpha = {\rm softmax}(\pmb e)\in \mathbb R^N$;
- 使用注意力分布计算注意力输出$\pmb a = \sum_{i=1}^N \alpha_i\pmb h_i \in \mathbb R^{d_1}$;
Attention的变体
在计算注意力分数$\pmb e$上有许多变体的方法:
- 基础点积attention:$\pmb e_i = \pmb s^\top \pmb h_i \in \mathbb R$
这种方法假设$d_1=d_2$,这也是我们前面看到的版本 - 乘法attention(Multiplicative Attention):$\pmb e_i = \pmb s^\top \pmb W\pmb h_i \in \mathbb R$
解决了上述$d_1=d_2$的问题,然而$\pmb W$的引入增加了参数规模 - 降级的乘法注意力(Reduced-rank Multiplicative Attention):$\pmb e_i = \pmb s^\top (\pmb U^\top\pmb V)\pmb h_i = (\pmb {Us} )^\top (\pmb V\pmb h_i)\in \mathbb R$
降低了$W$的参数规模,$\pmb U\in \mathbb R^{k\times d_2}$,$\pmb V \in \mathbb R^{k \times d_1}$,$k \ll d_1,d_2$,这也是Transformer的基础 - 可加性attention(Additive Attention):$\pmb e_i = \pmb v^\top {\rm tanh}(\pmb W_1 \pmb h_i+\pmb W_2\pmb s) \in \mathbb R$
将注意力变成神经网络的可训练形式,直接统一训练,$\pmb W_1\in \mathbb R^{d_3 \times d_1}$,$\pmb W_2 \in \mathbb R^{d_3\times d_2}$,$\pmb v\in \mathbb R^{d_3}$都是权重,其中$d_3$属于超参数。
Attention在各种网络中都有所应用,只需要满足其查找的基本要求就可以引入Attention机制提供部分关注的效果。

Attention是基于query的一种关注机制,对values的信息有选择进行加权加和,更高层的说,Attention可以理解为一个存储访问的系统,其中values在memory中保存,query是一种访问机制,Attention提供的是一种合理有效的推荐访问机制,给出的是最适合模型的分布结构。
自注意力机制(Self-Attention)
自注意力机制,顾名思义就是“自已关注自己”,前文提到的注意力机制是Decoder对Encoder的关注,其实际上是Decoder对外部信息的一个关注,query来自Decoder而values来自Encoder,而自注意力机制就是自己关注自己的输入,我的理解是Decoder是query,同时Decoder也是value,并且key也是Decoder。
(下附一个我认为讲的很好的博主的原文:Attention机制与Self-Attention机制的区别_selfattention_At_a_lost的博客-CSDN博客)
传统的Attention机制在一般任务的Encoder-Decoder model中,输入Source和输出Target内容是不一样的,比如对于英-中机器翻译来说,Source是英文句子,Target是对应的翻译出的中文句子,Attention机制发生在Target的元素Query和Source中的所有元素之间。简单的讲就是Attention机制中的权重的计算需要Target来参与的,即在Encoder-Decoder model中Attention权值的计算不仅需要Encoder中的隐状态而且还需要Decoder 中的隐状态。
而Self Attention顾名思义,指的不是Target和Source之间的Attention机制,而是Source内部元素之间或者Target内部元素之间发生的Attention机制,也可以理解为Target=Source这种特殊情况下的注意力计算机制。例如在Transformer中在计算权重参数时将文字向量转成对应的KQV,只需要在Source处进行对应的矩阵操作,用不到Target中的信息。
自注意力是注意力的一种,注意力机制解决了RNN中的一系列问题:
- 线性交互距离问题:距离的问题会导致较远的状态无法交流信息
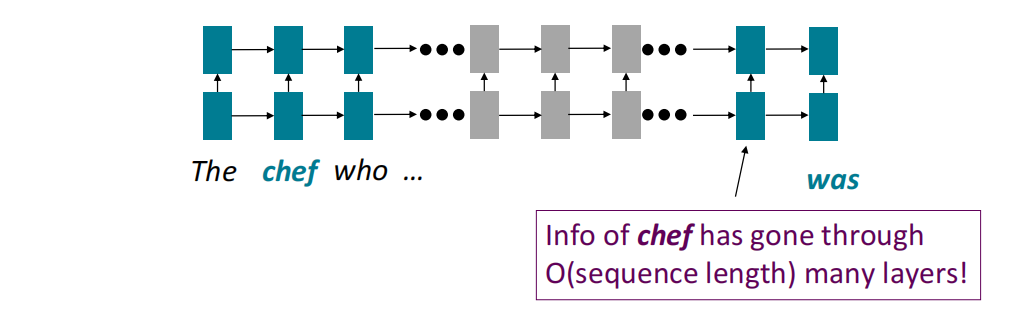
- 并行性缺失:在执行前向或后向传播时由于RNN的时序性,无法并行处理所有状态
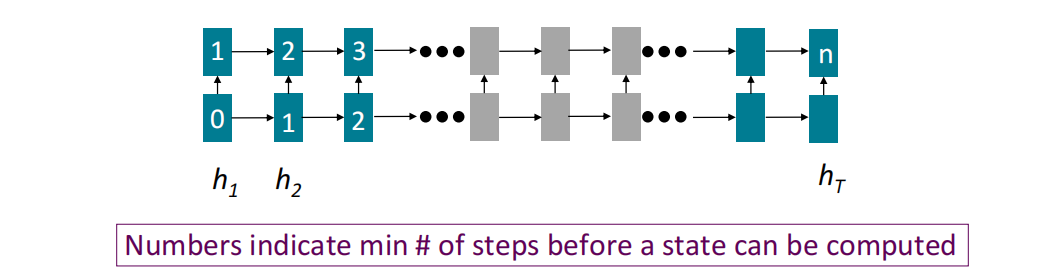
自注意力的大致结构如下:
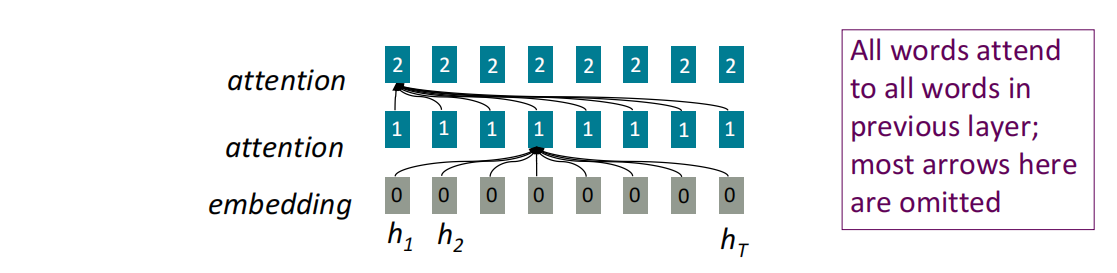
在自注意力的结构下,首先每个隐状态$h_i$在作为query时,其计算过程都是单独的,序列长度的增加不会引起不可并行操作数量的增加,且单词的交互距离为$O(1)$,因为每个单词都可以单独对每次单词做连接。
我们可以将Attention的过程看作对key-value对的一种模糊查找。
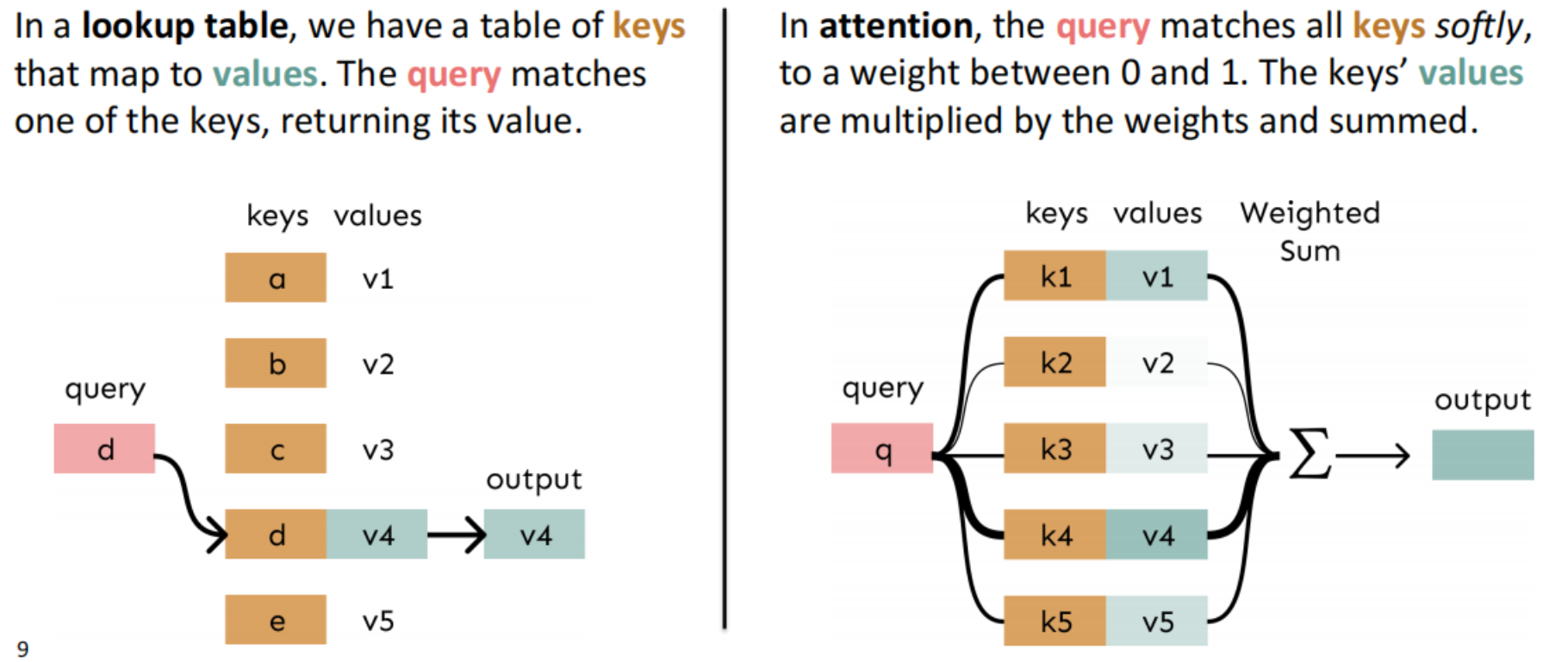
自注意力的keys、values和querys都来自于同一个语句序列,直观理解,querys表示对信息的查询请求,keys代表对信息的索引,values代表需要查询的信息,自注意力乃至注意力机制都是通过计算querys和keys的亲和度,从而找到最为适合的values,其中keys和values更像是键值对的关系。
定义语句为$\pmb w_{1:n}$,其中$\forall \pmb w_i \in V$。对于每个单词$\pmb w_i$,做词嵌入,令$\pmb x_i = E\pmb w_i$,其中$E\in \mathbb R^{d\times |V|}$是嵌入矩阵。自注意力需要计算以下内容:
用权重矩阵$Q、K、V\in \mathbb R^{d\times d}$变换每个词嵌入:
$$
\pmb q_i = Q\pmb x_i \ \ \ \ \pmb k_i = K\pmb x_i \ \ \ \ \pmb v_i = V\pmb x_i
$$计算注意力分布:计算键和查询之间的成对相似度并用softmax归一化(在key的维度上作归一化)
$$
\pmb e_{ij} = \pmb q_i^\top\pmb k_j \ \ \ \ \pmb \alpha_{ij} = { { {\rm exp}(\pmb e_{ij}) } \over {\sum_{j’} \exp(\pmb e_{ij’ } ) } }
$$计算每个单词的输出作为值的加权和:
$$
\pmb o_i = \sum_j\pmb \alpha_{ij} \pmb v_i
$$
Self-Attention的模块化处理
为了能够将self-attention用作模块来搭建网络,需要对self-attention加入一些细节,解决其模块化的障碍所在。
位置编码
自注意力在每个单词上都做一次注意力计算,在计算中并没有考虑单词的相对顺序,因为self-attention并不是建立在顺序信息中,故我们需要在我们的键、查询和值中编码句子的顺序。考虑将每个序列索引表示为一个向量,称之为位置编码:
$$
\pmb p_i\in \mathbb R^d, \ \ \ \ i\in{1,2,…,n}
$$
自注意力通过将位置编码的信息直接加到输入中,在深度自注意力网络中我们在第一层加入位置编码信息。
$$
\tilde {\pmb x}_i = \pmb x_i + \pmb p_i
$$
位置编码可以通过周期函数来进行实现,其中横轴为序列索引(1->n),横轴为维度d
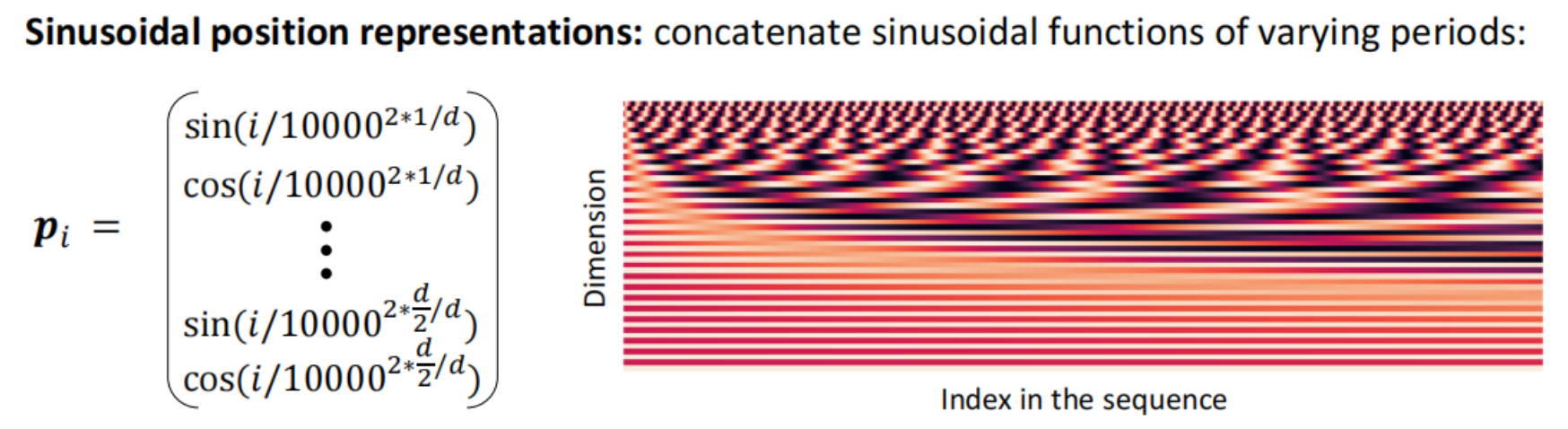
sin函数的周期性表明“绝对位置”可能不那么重要,我们只需要了解相对位置就可以实现将位置信息引入自注意力;而且,周期性的变化可以适配于长序列,因为函数可以多次回到起始点不断循环。但因为sin函数这样的周期性函数是模型开始时就规定好的,因此这个位置编码不可学习,无法实现动态调整。
因此,位置编码信息的学习被提出,令$\pmb p\in \mathbb R^{d\times n}$为可学习的参数,并令$\pmb p_i$为每个矩阵的列,让模型学习绝对位置表示。可学习的位置编码具有灵活可调整的特性,但其无法推断出超过index范围的编码(如n+1),目前,人们仍然在位置编码领域有所研究,现有研究有线性相对位置编码(相对位置)、基于依赖语法的位置编码(加入人类理解)等。
非线性模块
自注意力的本质是先计算注意力分布后取平均,其本身没有非线性部分加入,非线性的部分可以为网络加入更多的表示能力。其中一种简单的解决方法:为每个输出向量添加一个前馈网络: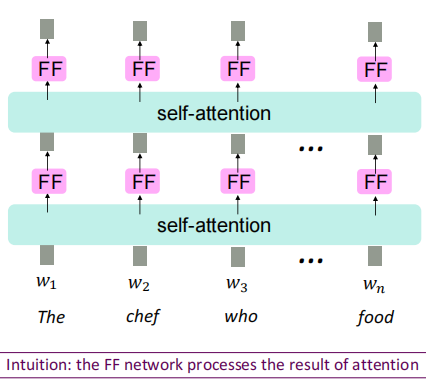
$$
\pmb m_i = {\rm MLP(output_i)} = \pmb W_2 \times {\rm ReLU}(\pmb W_1 \times {\rm output} _i+\pmb b_i)+\pmb b_2
$$
自注意力掩码(解码器)
要在解码器中使用自注意力,由于其作为语言模型需要严格从一个方向(从左到右)做预测,因此未来的一些信息是在自注意力中不能看到的,因此需要引入掩盖的技术来关掉自注意力在未来部分的视野。
对自注意力视野的掩盖,比较直观的方法是在每个时间步中,更改key和query,以只包括过去的单词,但是这种方法效率很低,而且比较难并行训练,为了实现并行化,我们通过将注意力分数设置为$-∞$来屏蔽对未来单词的注意力。
$$
\begin{cases}
\pmb e_{ij} = \pmb q_i^\top \pmb k_j,\ \ \ \ j\le i \\
\pmb e_{ij} = -∞, \ \ \ \ \ j >i
\end{cases}
$$
自注意力掩盖可以形象为以下表示:
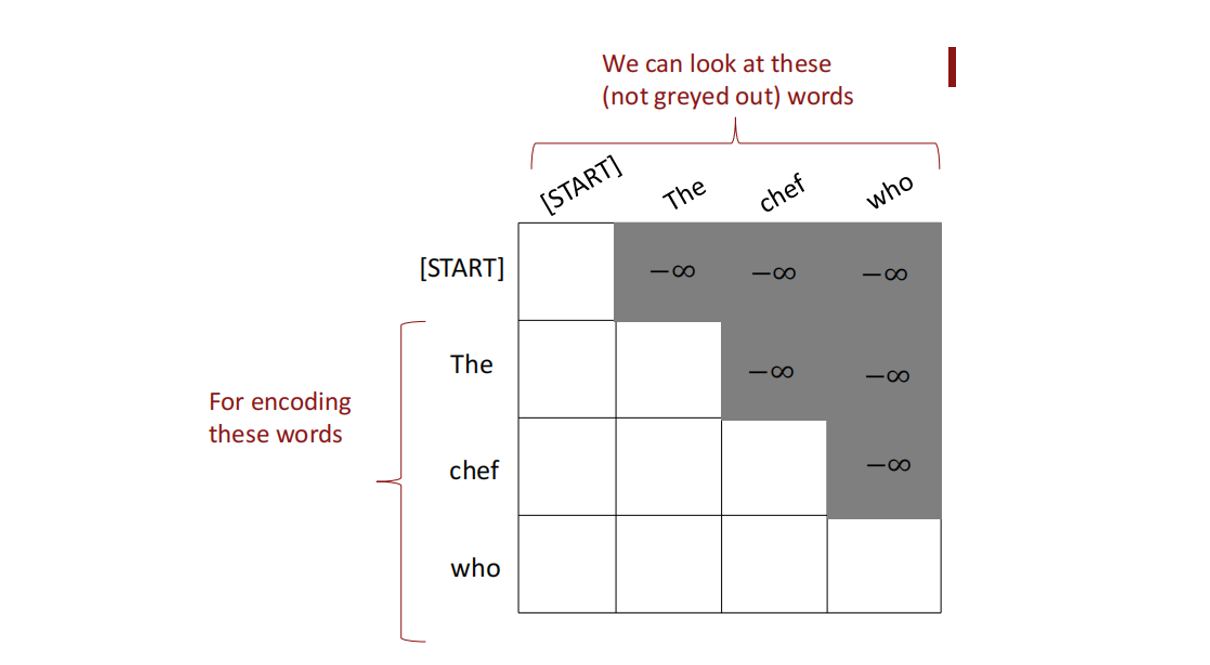
综上所述,对于自注意力中有关模块化训练的一些问题都对应进行了解决。
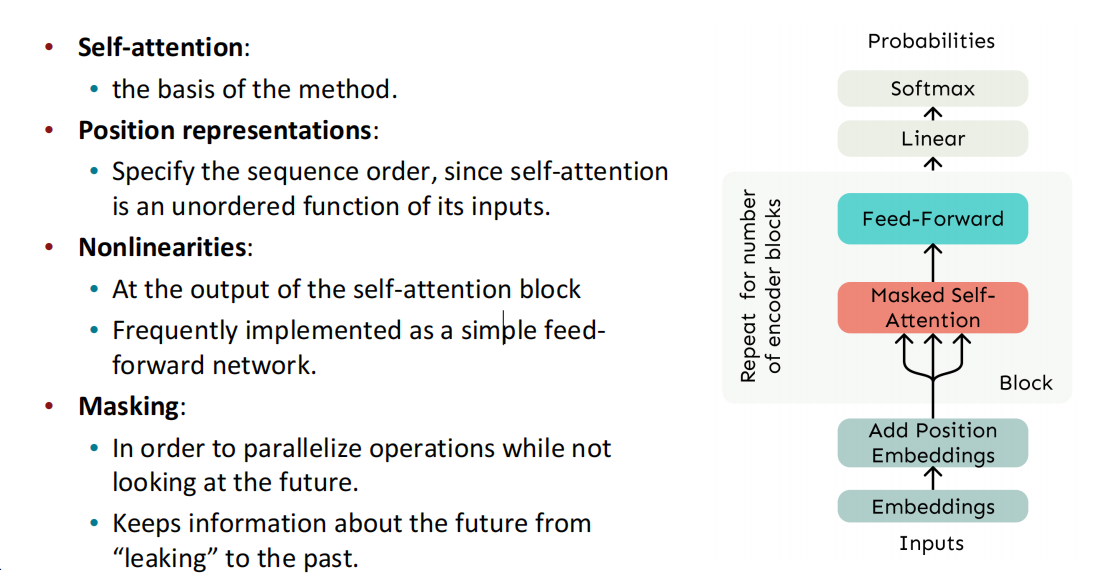
Transformer
Transformer解码器是我们构建语言模型等系统的方法。它很像我们最小的自注意力架构,但有更多的组件,其中嵌入和位置嵌入是相同的。
注意力的堆叠
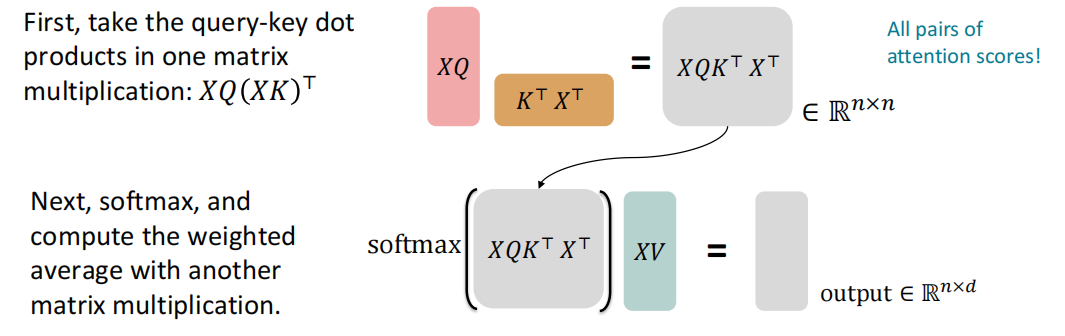
首先,为了能够使得注意力作为模块被使用,我们需要将上文中提到的注意力计算变成矩阵计算的形式,从而提高计算效率,实现并行计算的愿景。对于key-query-value 注意力来说计算过程如下:
- 令$X=[\pmb x_1,…,x_n]\in \mathbb R^{n\times d}$为输入向量的连接
- 记录$XK\in \mathbb R^{n\times d}$、$XQ\in \mathbb R^{n\times d}$和$XV\in \mathbb R^{n\times d}$
- 直接计算注意力输出${\rm output} = {\rm softmax}((XQ(K^\top X^\top))XV \in \mathbb R^{n\times d}$
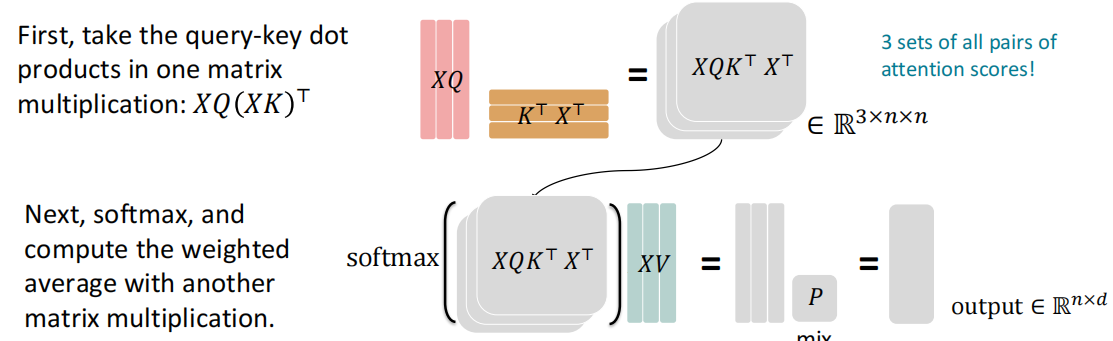
多头注意力机制(Multi-head Attention)
假设我们想一次查找句子中的多个位置,而简单自注意力每次只关注Q和K最为亲和的一个,因此这时就比较难以完成任务。多头注意力旨在引入多个Q-K-V来实现多个部分的查找。令$Q_l,K_l,V_l \in \mathbb R^{d\times {d \over h} }$,其中h代表注意力头的数量,$l\in \lbrace 1,…,n \rbrace$。这时,多头注意力的计算过程就变成了:
- 令$X=[\pmb x_1,…,x_n]\in \mathbb R^{n\times d}$为输入向量的连接
- 记录$XK\in R^{n\times {d \over h} }$、$XQ\in R^{n\times {d \over h} }$、$XV\in R^{n\times {d \over h} }$
- 计算注意力输出${\rm output}_l = {\rm softmax}(XQ_l(K_l^\top X^\top))*XV_l \in \mathbb R^{d \over h}$
- 将输出拼接起来${\rm output} = [{\rm output}_1;…;{\rm output}_h]Y$,其中$Y\in \mathbb R^{d \times d}$,这个$Y$的作用我的理解是多头注意力的一个简单加权。
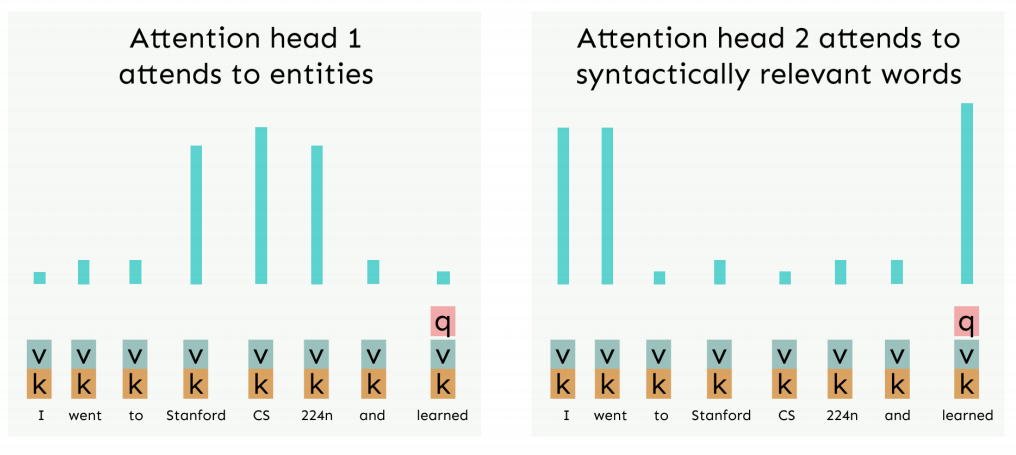
在多头注意力中,每个注意力头都分别关注句子中的不同层面,比如语法结构、实体本身等等。
Transformer的训练技巧
为了能够更有效的训练Transformer,一些必要的技巧(trick)需要引入,但这些技巧不会影响训练本身的结果
缩放点积(Scaled dot production)
缩放点积技巧引入的原因在于点积本身的增长和维度$d$有关($d$会和加权计算的次数相关),这会使得点积作为softmax函数的输入可以很大,从而过分挤占其他部分的梯度空间,使得梯度十分小。因此对于点积的部分,除以一个缩放量$\sqrt{d/h}$
$$
{\rm output}_l = {\rm softmax}({ {XQ_l(K_l^\top X^\top)} \over {\sqrt{d/h}} })*XV_l \in \mathbb R^{d \over h}
$$
残差连接(Residual connections,Add)
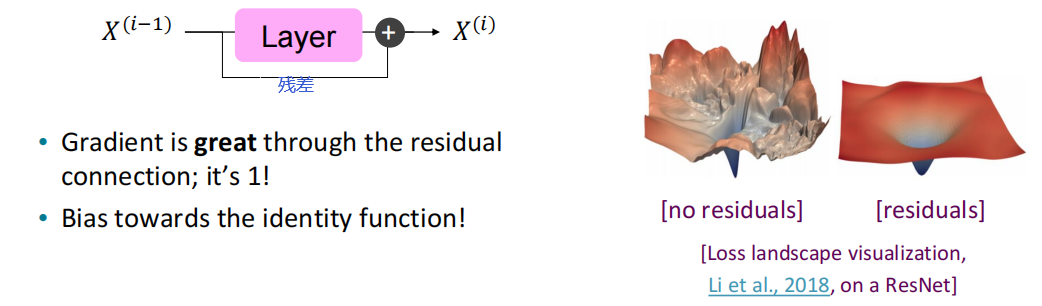
残差连接是帮助模型更好训练的一个技巧。残差连接主要解决梯度消失的问题,是一种经典的训练技巧,假设我们的模型是输入经过一个很复杂很复杂的函数获得输出
$$
X^{(i)} = {\rm Layer}(X^{(i-1)})
$$
引入残差连接,直接将输入和输出相连,只需要学习上一层的“残差”
$$
X^{(i)} = X^{(i-1)}+{\rm Layer}(X^{(i-1)})
$$
层归一化(Layer normalization,Norm)
层归一化是一种帮助模型训练更快的技巧。层归一化的想法是希望通过归一化为每层内的单位均值和标准差来减少隐藏向量值的无信息变化。LN就是在每个样本上统计所有维度的值,计算均值和方差,当我们使用梯度下降法做优化时,随着网络深度的增加,数据的分布会不断发生变化,为了保证数据特征分布的稳定性,我们加入Layer Normalization,这样可以加速模型的收敛速度。
层归一化的思路在于对样本本身做归一化,$x\in \mathbb R^{d}$表示模型中的单个(词)向量,层归一化需要计算出样本在所有维度上的均值和方差(标准差):
$$
\mu = \sum_{i=1}^d x_i, \ \ \ \ \sigma = \sqrt{ {1 \over d} \sum_{i=1}^d(x_i-\mu)^2},\ \ \
$$
其中$\mu,\sigma\in \mathbb R$。层归一化引入了增益项$\gamma \in \mathbb R^d$和偏差项$\beta \in \mathbb R^d$,这两个参数都是可学习的参数,层归一化的输出为:
$$
{\rm output} = { {x-\mu} \over {\sqrt{\sigma^2+\epsilon} } }*\gamma+\beta
$$
Transformer的Encoder和Decoder
在Transformer的Encoder和Decoder中,我们都采用了位置编码-多头注意力-Add&Norm-前馈网络-Add&Norm的结构,其中Decoder的注意力中加入mask来实现单向语言模型。实际上在Transformer建构时,Decoder对于Encoder的回顾主要是交叉注意力,因此这里需要引入交叉注意力的概念。
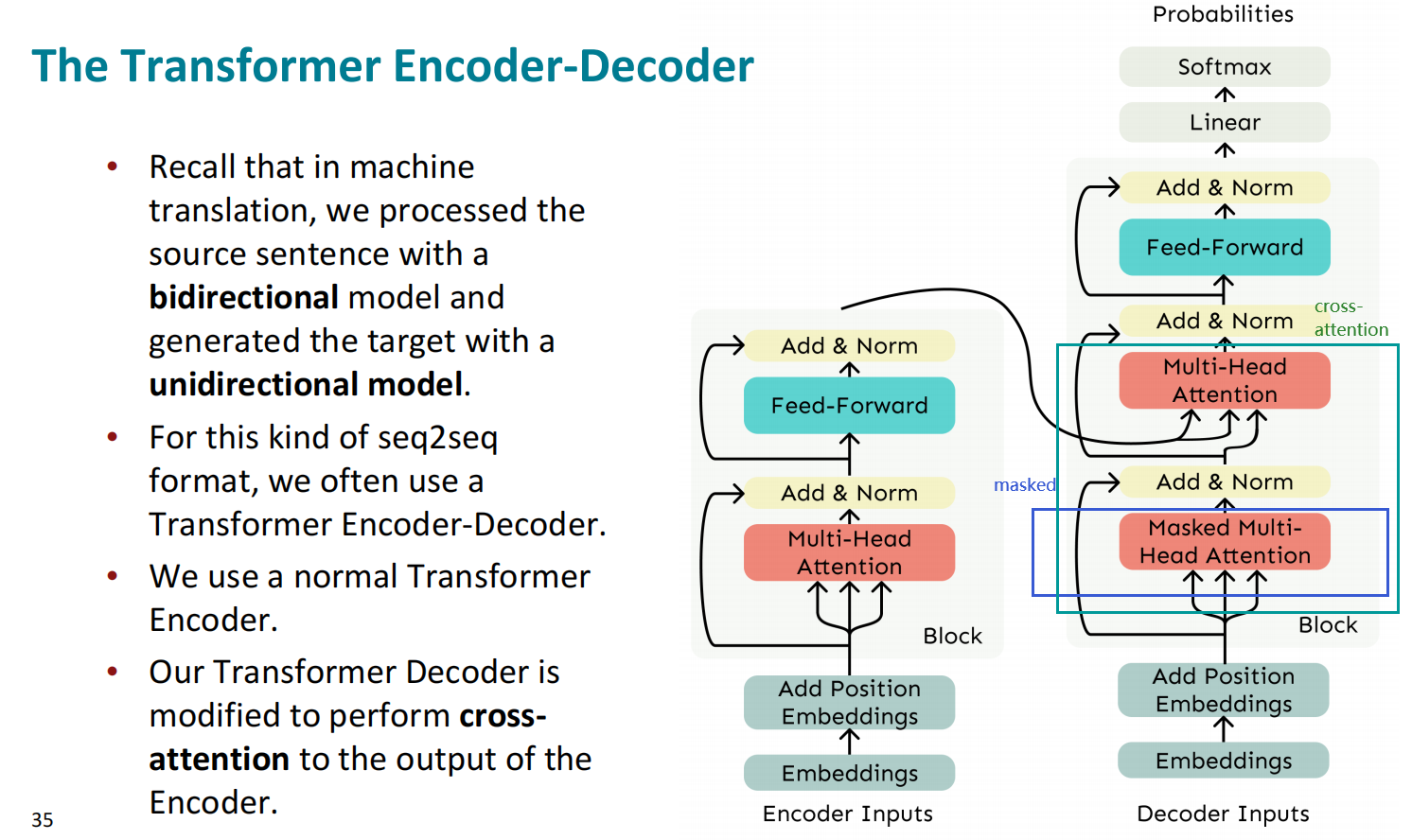
交叉注意力
交叉注意力用于像上文提到的Seq2seq这样的Encoder-Decoder结构,而在Transformer结构中也采取了这样的方式,这需要Decoder对Encoder的信息进行回顾,这种回顾的机制融入到了注意力参数生成本身。
令$\pmb h=\lbrace \pmb h_1,…,\pmb h_n\rbrace,\pmb h_i\in\mathbb R^d$为Encoder的输出,$\pmb z = \lbrace \pmb z_1,…,\pmb z_n\rbrace \in \mathbb R^d$为Decoder的输入,交叉注意力的key和value来自于Encoder:
$$
\pmb k_i = K\pmb h_i,\ \ \ \ \pmb v_i = V\pmb h_i
$$
交叉注意力的query来自Decoder:
$$
\pmb q_i = Q\pmb z_i
$$
这样就实现了之前的那种通过Decoder的query来查找Encoder的value的效果了。
Transformer的表现
由于Transformer的高可并行性,基于Transformer的训练就可以使用预训练模型进行微调,以高效实现任务,因此目前在比较受欢迎的benchmack平台GLUE上,各个任务排名靠前的模型基本都是Transformer为基础的模型。
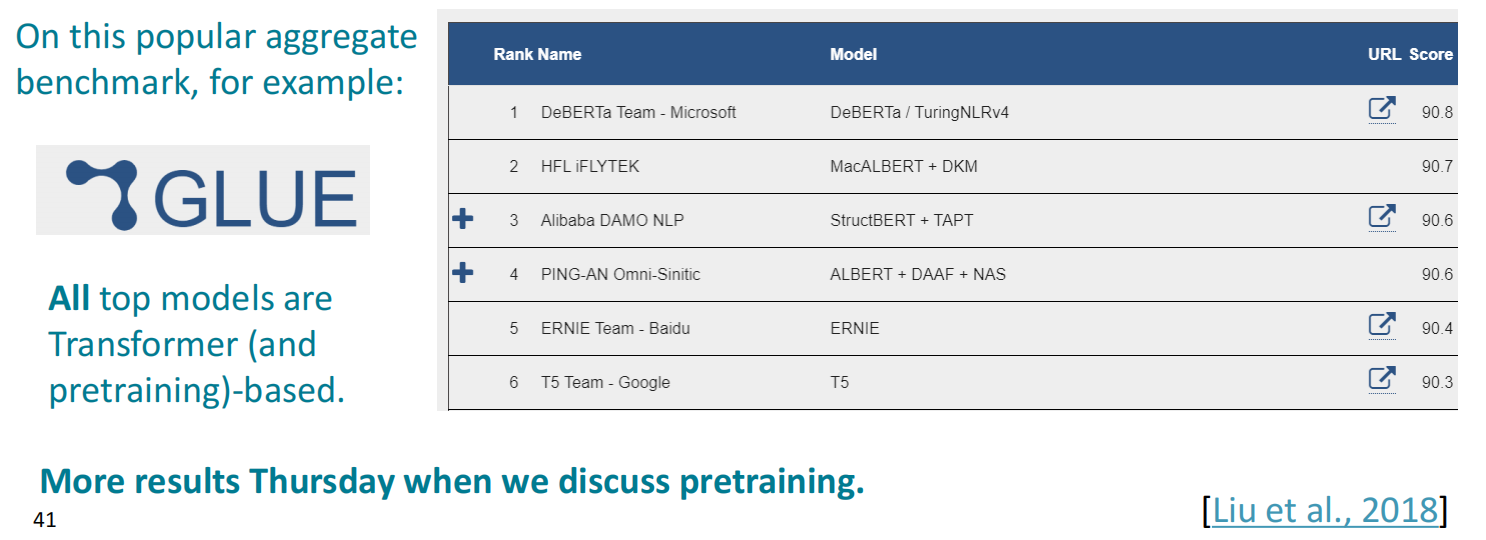
Transformer的缺点
Transformer尽管有着十分高效的训练速度和强悍的表现,但其在参数上还是有一些缺点在
- 计算量会随着序列长度的增加而二次单位的增大(每个单词都得和其他所有单词连接一遍)

- 简单的绝对下标作为位置编码可能不太和人类的阅读习惯相匹配
对于第一点,现有工作中已经开始针对其进行研究,比较主流的是将序列长度中针对Key和Value的部分映射到低维空间降低计算量。
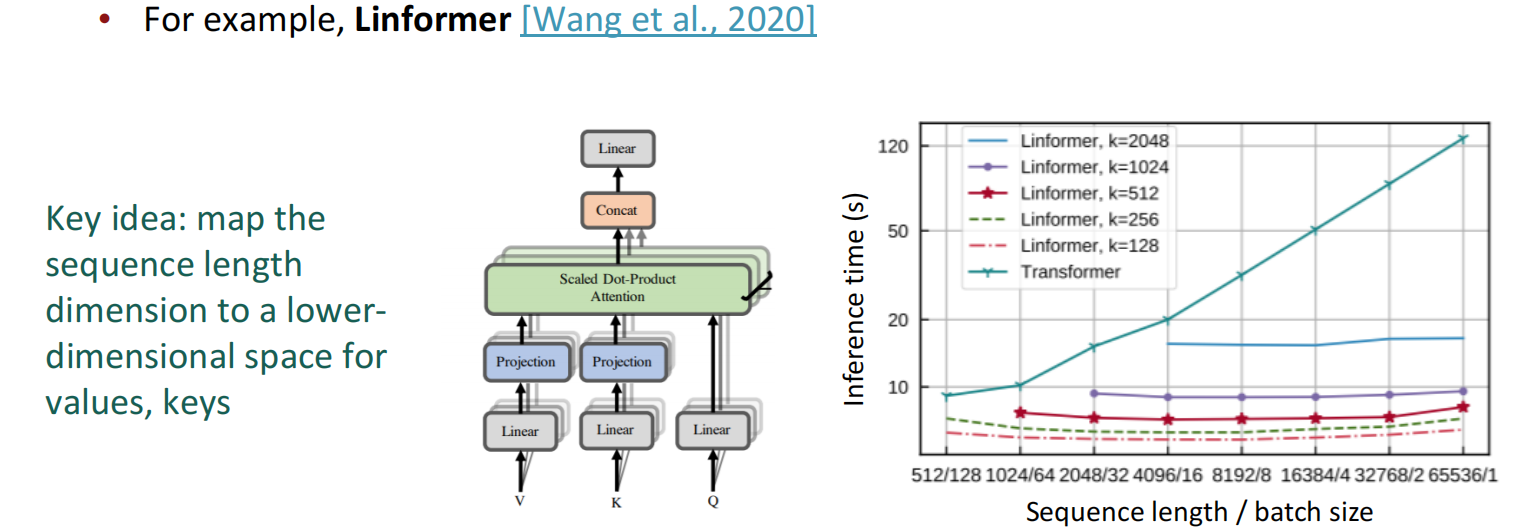
实际上,几乎没有大型 Transformer 语言模型使用我们在这里展示的二次成本注意力,都是用的成本相对更低的注意力模型,但其在大型数据上的效果往往不太好,这需要对低成本注意力或大规模数据做继续研究。

课后问题
Q:自注意力和前馈神经网络都进行了全连接,这两个有什么不同
A:不同有二:一是前馈神经网络的权重是随着训练不断迭代的,而自注意力的注意力值会随着内容的变化而变化,是动态的;二是自注意力提供了一种生成归纳偏置的一种机制(不太懂)
Q:Decoder的掩码是只在第一层用还是对所有都用
A:都用,只有都掩盖掉,未来的信息才不会在任意一个层中泄露。